Математическое моделирование поверхностных гравитационных волн в водохранилище узко-каньонного типа

Как правило, водохранилища в горных местностях строятся в сильно зауженных каньонах ущелий рек. В них часто вторгаются селелавинообразные потоки либо обвальнооползневые массивы. В результате вторжения с большими скоростями в водохранилищах и хвостохранилищах образуются высокие гравитационные волны, часто приводящие к большим стихийным и экологическим бедствиям в виде разрушений, человеческих жертв и загрязнений окружающей водохранилище территории веществами, годами накопленных в хвостохранилищах горно-обогатительных предприятий. В связи с этим проектировщики и эксплуатационные службы обязаны оценивать потенциально возможное повышение уровня воды у плотины и объем перелитой воды через створ плотины, а также зону и степень затопления и загрязнения местности в нижнем бьефе в зависимости от геометрических, кинематических и динамических характеристик потенциально возможных обвально-оползневых масс, селе и лавинообразных потоков. Таким путем можно спрогнозировать, а затем предотвратить либо уменьшить те последствия и ущерб, которые может вызвать образование разрушительных волн.

Однако, надо отметить, что до настоящего времени не существует доступного проектировщикам и эксплуатационным службам надежного метода и формулы для вычисления амплитуд образованных волн в водохранилищах узко-каньонных типов, характеризующихся большими глубинами воды и непризматическими конфигурациями.

В настоящей статье дается попытка заполнить этот пробел путем постановки и решения начально-краевой задачи волновой гидродинамики и гидравлики, в которой наиболее адекватно отражены гидродинамические и гидравлические процессы, имеющие место при отмеченных выше стихийных явлениях, а также геометрическая конфигурация водохранилища.

Предположим, что в прямоугольной системе координат Oxyz часть пространства, ограниченная условиями 0 6 x 6 L, — B ( x,z )/‘2 < y < B (x, z)/2 , — H 6 z 6 0 , представляет узко-глубокое непризматическое водохранилище, расположенное в горном регионе.

Ось oz направлена вертикально вверх, H — глубина воды в водохранилище, L — длина, B ( x, z ) — ширина водохранилища. На рисунке ниже представлены поперечный профиль и плановое очертание водохранилища.

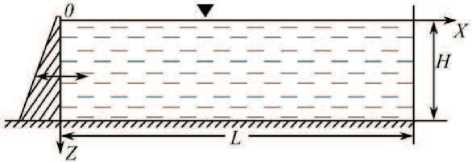
Расчетная схема поставленной задачи

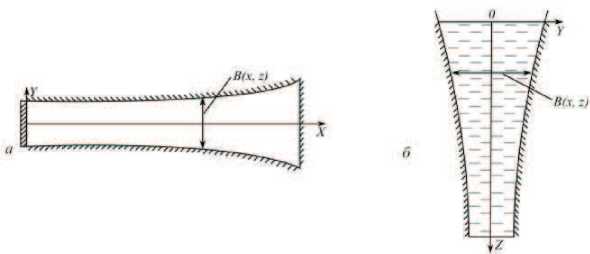
Плановая (а) и глубинная (б) конфигурации водохранилища

Рассмотрим волновое движение воды, вызванное тем, что с боковой грани водохранилища в него вторгается обвально-оползневой массив горной породы либо селелави-нообразный поток. Считая движение воды безвихревым, потенциал средней по ширине водохранилища скорости должен удовлетворять следующему дифференциальному уравнению [1–3]:

д ² ^ д 2^      1 дB ( x,z) д^ 1 dB (x,z) д^ q ( x,z,t)

дx2 дz2 B(x,z) дx дx B(x,z) дz дz B^z) , где q(x, z, t) — скорость вытеснения воды обвально-оползневым массивом либо интенсивность вторжения в водохранилище селелавинообразного потока.

Через единичную функцию Хевисайда интенсивность q ( x, z, t ) аналитически выражается следующим образом:

q ( x, z, t ) = Uo [1(x — (xo — a)) — 1(x — (xo + a))]

x

1 ^z + z0 + 2^ — 1 ^z + zo —

DI

[1(t) — 1(t — to)] ,

где 2a — ширина по фронту обвально-оползневого массива, xo — абсцисса ее центра, h — мощность обвально-оползневого массива либо глубина селелавинообразного потока, t0 — продолжительность времени вторжения.

Средняя скорость вторжения вычисляется так:

W0

2 ahto ¹

где W0 — объем вторгшегося массива либо селелелавинообразного потока.

В соответствии с физико-механической сущностью задачи, для дифференциального уравнения (1) ставятся следующие начальные и граничные условия [1–3]:

^ ( x,z,t )V t =- = 0,

d^(x, z, t ) ∂t

= 0,

t =0

d^(x, z, t ) ∂x

= 0,

d^(x, z, t)

∂x

= 0,

/ d2^(x,z,t) + d^(x,z,t) \

∂t ^{2        g} ∂z

= 0, z=0

d^(x, z, t ) ∂z

= 0.

z = - H

Дифференциальное уравнение (1), начальные условия (4), граничные условия (5) и (6) в совокупности представляют начально-краевую задачу математической физики и математически моделируют волновое движение воды в узко-глубоком непризматическом водохранилище, когда волны образуются в результате вторжения в водохранилище обвальнооползневого массива либо селелавинообразного потока. Непризматическая конфигурация водохранилища в плане и по глубине в составленной модели отражены через ширину водохранилища, т. е. через функцию B ( x,z) , которая зависит как от продольной горизонтальной координаты x , так и от вертикальной координаты z .

Коэффициенты дифференциального уравнения (1) являются переменными, и это создает большие математические трудности при попытке аналитического решения поставленной начально-краевой задачи.

Надо отметить, что дифференциальное уравнение (1) впервые получено в работе [4]. В классической линейной теории поверхностных гравитационных волн потенциал скорости должен удовлетворять дифференциальному уравнению Лапласа как для пространственных, так и для двумерных волн [2–4], см. также [5]. В представленной модели (1)–(6) описываются средние по ширине трехмерные волны, т. е. фактически двумерные волны. Научной новизной этой модели является то, что в нее в гидродинамико-гидравлическом приближении через функцию B (x, z) увязаны наиболее характерные параметры естественного очертания водохранилища узко-каньонного типа.

Приступив к решению начально-краевой задачи, вначале принимаются некоторые предположения, упрощающие путь ее решения. Так, например, будем полагать, что ширина водохранилища аппроксимируется следующей экспоненциальной функцией

B(x,z) = B-e s ^{1 x+s} 2 ^z .                                    (7)

Кроме этого в дальнейшем будем полагать, что q(x,z,t) = qi(x) • q2(z) • q3(t),                                     (8)

q1(x)	= 10,,	x- — a < x < x- + a, 0 < x < x- — a, x- + a <  x < L;
q2(z)		— z 0 — h < z <  - z- + h , —H < z < —z- — 2, —z- + 2 < z <  0;	(9)
q3(t)	= (U-	0 < t < to, t>t .

В результате применения подстановки s1 s2

^(x,z,t) = ^(x,z,t)e 2 ^x 2 ^z ,                             (10)

начально-краевая задача (1)-(10) относительно функции '(x, z, t) принимает следующий

вид:	∂ 2 ψ ∂ 2 ψ     s 2 1 s 2 2 dx 2 + dz 2 -    + )*	= qi(x>2( z )q3( B0	t)  _S1T e 2 x 2 z ,	(11)
	v'=dt=	0,       t = 0,
	I dV - ?■ ' l x- '*	( dx - 1 * )	= 0, x = L	(12)
	(^ + ^ — gy* ) z „^	- 0, ( - S2	')      = 0. z = - H

Введем функцию Ф(x, z, t ) и дифференциальные операторы D, Di, Di

Ф (x,z,t) = d'(dxz,^> - si',	(13)
D=dL+dt _( si, si 1 D dx 2 + dz 2 V 4 + 4 J ’	(14)
D i = d^ti+gdz- gs1 ,	(15)
∂    s2 D 2 = dz -  .	(16)

Применив линейные дифференциальные операторы D, D1 , D2 последовательно к обеим частям (13) и учитывая выражения (11)–(12) относительно введенной функции Ф(x,z,t) , получим:

D№ = q^zlq?^ s2 4 АЛ1(х)е s2 Л — siq^e s1 xl,

Bo            [ax \          У2J

Ф ' 4„L = 0,

Di [Ф]к_0 = 0, D2[4]|z=-H = 0.

Для решения начально-краевой задачи (17)–(19) последовательно применяются интегральное преобразование Лапласа по времени t и разложение в ряды Фурье по переменной x в интервале (0, L)

Ф(x, z )

+∞ j (       -'

∞

Ф(x,z) = ХФ п ( z )

n =1

sin ППх.

Для функции Фn(z) получается обыкновенное дифференциальное уравнение с двумя граничными условиями

d ² Ф n dz ²

- ^ п ^Ф n = "|r^q2^{(z)e 2} z ^a n , B0

[(p2 - gW n ⁺gddz n]

= 0,

( dФ n dz

-

S2 e A

2 ^Ф n)

= 0, z = - H

где

А » = V" 5 + st + si -

nπ a n = T,

x o + a

_ 2Uo  [ an   L J e x0-a

s ₁

² x sin a n x dx.

В результате решения краевой задачи (22)-(23) определяется функция Ф » (z) , n = 1, 2, 3,...

Далее обратным ходом сначала определяется функция Ф » (x, z) из (21), а затем ее оригинал Ф(х, z, t) . При этом для определения оригинала достаточно таблицы операционного исчисления. После определения Ф(х, z,t) из выражения (13), как из обыкновенного дифференциального уравнения, определяется функция ^(x,z,t) . Наконец, при известной функции ^(x,z,t) из выражения (10) определится потенциал скорости ^ ( x,z,t ) и, следовательно, поставленная начально-краевая задача решена.

Уравнение волновой поверхности получается дифференцированием потенциала по времени

n(x,t)

1 d^(x, z, t)

g ∂t

z =0

Окончательно для уравнения свободной волновой поверхности получаются следующие выражения:

где

s ₁

n(x, t) = e 2 ^x

si     w(t)

Boe s ^{1 L} - 1

∞

- X n=i

A n K n(S 1 sin a » x + a » cos a » x)

(1 + 2  th X n HHx » - s2)

f n (t)

K n

α n

2BoA »

^A n - s ² )( z ^{o +} h ) — _e — ( ^An— 2 )( z ⁰ — h )

2 A n H - (a„ + s ²²) (zo +2))

2 A n H - ( A n + s ²² )( z o - h ))1       ²

I 1 + e — 2 A n H ,

2 a » = L

e 2 ¹ ( x ^o a ) sin a _n (x ₀ — a) — e   21 ^{(x o +a)} sin a _n (x ₀ + a)j,

f » (t) =

JUo sin Y » t,                    0 < t < to,

(2Uo sin Y nt 0 cos Y » ( t — t 0 ) , t > to;

w(t) =

J 2ahUot,

I 2ahUoto,

0 < t < t _o , t > to;

Yn = ^

gA„ (th A „ H + ^ An) — gs - (1 + 2 5 2П th A „ H)

1 + ^n th A » H

, n = 1, 2, 3,...

Полученные расчетные выражения (25)–(30) легко реализуются на ЭВМ. Результаты численных экспериментов позволяют определить амплитуды образованных волн в водохранилище в зависимости от геометрических габаритов водохранилища и от кинематических и динамических характеристик вторгшегося селелавинообразного потока либо обвально-оползневого массива.