Математическое моделирование процесса диффузии жидких добавок внутрь экструдированных гранул комбикорма для рыб ценных пород

Низкая питательность и несбалансированный состав, высокая крошимость и низкая водостойкость гранул отечественных комбикормов отрицательно влияют на продуктивность рыбы [5, 8]. Одним из перспективных направлений повышения качества комбикормов для аквакультуры является замена животного белка и жира на растительные компоненты [10]. АО «НПЦ «ВНИИКП» в результате выполненных исследований разработана перспективная технология комбикормов, в которых осуществлена замена дорогостоящих белковых компонентов животного происхождения (рыбная мука, мясокостная мука, кровяная мука, субпродукты и т. п.) на растительные высокобелковые компоненты (соевый, подсолнечный или рапсовый шрот, люпин, горох, соя и т. п.), подвергнутые экструзионной обработке, и вакуумное нанесение с последующей диффузией жидких компонентов (растительное масло, рыбий жир и т. п. внутрь экструдированных гранул.) [6, 7]. Это позволило снизить количество рыбной муки в рецепте с 40 до 21% без снижения продуктивных свойств экструдированных кормов.

Применение вакуумного напыления жировых компонентов на экструдированные комбикорма для ценных пород рыб привело к возможности повышения содержания жира до 40%, стабилизации питательных качеств комбикорма; снижению дробления комбикормов на 10%; улучшению физических качеств готового комбикорм (влажность 10–12%); повышению уровня проникновения жидких компонентов на 25–30%; сохранению сухой поверхности экструдата; снижению патогенной микрофлоры до 0 [9].

Разработаны система вакуумного напыления, с помощью которых возможен ввод жидких компонентов до 42% без ущерба для характеристик текучести готового продукта. Вакуумное напыление делает возможным обеспечение гораздо большей точности ввода компонентов, а также обеспечивает гораздо лучший показатель коэффициента вариации в сравнении с процессом непрерывного типа.

Процесс вакуумной пропитки можно регулировать, исходя из того, какому виду и возрасту рыб предназначается корм, чтобы они в разные периоды жизни получали больше витаминов и энзимов для улучшения состояния здоровья.

Размеры пористых экструдированных гранул комбикормов следующие: диаметр от 1.2 мм до 4.0 мм, длина гранул от 12–15 мм до 30–40 мм. Диффузия жировитаминной добавки внутрь гранул происходит при ламинарном режиме движения.

Жилин А.А. и Федоров А.В. [1] исследуя динамику изменения влаги в сечениях x = 10, 20, 90 мм в брусе из пористого материала длиной 100 мм, использовали для описания исследуемого процесса уравнение нестационарной диффузии д W дt

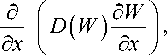
где D ( W ) – коэффициент диффузии; W – влажность; t – время; x – пространственная координата.

Решение данной задачи проводилось численно методом пристрелки в два этапа.

В результате было получено распределение влажности в рассматриваемых сечениях в зависимости от времени. В каждом сечении на профиле влажности можно выделить три участка. Начало первого участка, на котором значение влажности равно нулю, соответствует моменту начала эксперимента, конец – моменту достижения волной влажности рассматриваемого сечения. На втором участке происходит постепенное увеличение влажности до значения W к . Третий участок, как и первый, характеризуется постоянным значением влажности, равным W к .

Мейрманов А.М. и др. [2] рассмотрели две модели диффузии в пороупругой среде, состоящие из системы уравнений Стокса, которые описывают движение несжимаемой вязкой жидкости в поровом пространстве и системы уравнений Ламе, описывающих колебания несжимаемого твердого скелета. Рассматриваемая система дополняется конвективным уравнением диффузии для примеси в жидкости. Получены новые корректные математические модели, моделирующие процесс диффузии в пороупругой среде посредством усреднения и метода двухмасштабной сходимости Нгуетсенга.

В работе [3, 4] предложено кинетическое уравнение типа Колмогорова–Феллера с дополнительной координатой, описывающее как диффузионный, так и субдиффузионный мас-соперенос. Поскольку это уравнение является дифференциальным по времени и допускает параметрическую зависимость ядра W ~ от t , оно может быть полезно при моделировании нестационарных процессов, в том числе сопровождающихся сменой режимов переноса.

Материалы и методы

Решение дифференциального уравнения молекулярной диффузии жидких добавок в экструдированных гранулах описывается уравнением:

д c   гх (2 д ² c   д ² c д ² c ²

--= D _т —7 +--7 +--7

дт     ^д x ²    д у ²    д z ² _?

с граничными условиями третьего рода (при условии поглощающей (адсорбционной) поверхности т. е. когда с г.пов = 0) :

- D т f^ 1 = в ( с г - с гпов ) = в с Г      (2)

<5n ) n и начальными условиями

с ( x , y , z , 0 ) = c 0                (3)

Примем, что в процессе диффузии жидких добавок внутрь экструдированных гранул температура гранул и их теплофизические характеристики не изменяются, тогда для математического описания такой задачи используем решение нестационарной молекулярной диффузии в телах определенной геометрической формы (неограниченный цилиндр). В допущении постоянства концентрации жидких добавок, т. е. с г.пов = const , решение имеет для неограниченного цилиндра (таким телом можно считать экструдированные гранулы) следующий вид

экструдированных гранул. Тогда граничные условия III рода трансформируются в граничные условия I рода и процесс диффузии жидких добавок в экструдированные гранулы определяется только физическими размерами гранулы.

Тогда для рассматриваемого случая уравнение (4) с учетом тог, что концентрация жидких добавок на оси цилиндра (экструдированных гранул) ( Х = 0), принимает вид:

Q x = 0 =

- 4 ^ ( - 1 ) n ^{+ 1}

п ² (2 n - 1)^COS

( 2 n - 1 )

-—-—- nX exp

2 n - 1

п ²Fo

_M       ^2sin Pn     _x

Q = ^с Х = 1 ^- с = j^ ^ + sin ^ cos ^       ,   (4)

с Х = 1      n = 1 ^x( cos ( M n X ) exp ( - A 2 Fo ) )

Так как с _гп = с х = 1 = const , то при Х = 1 Q = 0 .

Учитывая, что при Fo >  0,3 ряд (5) быстро сходится, поэтому, отбрасывая все члены ряда, кроме первого, получаем следующее уравнение:

^Q x = 0 == -exp

П

—

п 1 с Fo

2 J

.

где в соотношениях (1)–(4) : с – концентрация жидких добавок в экструдированных гранулах; с _{г п} = с х = 1 - концентрация жидких добавок в экструдированных гранулах на их поверхности, равновесная с концентрацией жидких добавок в аэрозоле (диспергируемой среде) на поверхности гранулы; ( 5 с_г / 0n ) - градиент концентрации жидких добавок в непосредственной близости от поверхности гранул; D_T - коэффициент молекулярной диффузии жидких добавок в экструдированных гранулах, м/с; с 0 – начальная концентрация жидких добавок в экструдированных гранулах ( с о = 0 ); в — коэффициент массоотдачи, м/с; Q = ( с_Х = 1 - с ) /с_Х = 1 - безразмерная концентрация жидких добавок в экструдированных гранулах; X = х/5 - безразмерная координата; p n - представляет собой корни характеристического уравнения ctg p n = p _n/ Bi ; Bi = PS] D_т - число Био; Fo = D _тт| 5 - критерий Фурье или безразмерное время; 5 = 2 r половина толщины гранулы, м.

Результаты и обсуждение

Проведенные исследования при значениях критерия Bi > 100, показали что концентрация жидких добавок на поверхности экструдированных гранул становится равной равновесной концентрации аэрозоля жидких добавок, т. е. равной константе ( с _гп = с х = 1 = const ) .

Полученные значения критерия Био ( Bi ^ да ) показывают высокую интенсивность осаждения частиц жидких добавок на поверхность

Логарифмируя выражение (6) и решая его относительно критерия Фурье, получим:

,        4 , ( 4     1

Fo = ^-lnl п2  < п Qx =0

Уравнение (7) можно записать:

или т =

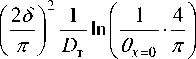
1 ( 14

— In l--- ^т  I ^Q x = 0 ^п

D т

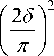
С помощью формулы (9) определяем численные значения коэффициентов диффузии Dт , используя для этого время и концентрацию жидких добавок на поверхности экструдированные гранул cт*.п и сх=1 в центре цилиндра (гранулы) (х = 5) сх=0 = с.

Для вычисления критерия Био необходимо определить коэффициент массоотдачи р .

Для данного эксперимента (при d ч = 1.2 · 10^-7 м, D т = 3.3x10 -7 м/с, t _ч ⁺ = 2.66 • 10 ^{- 4}, Sc = 75, Re = 850, Х = 0.47, U о = 0.022 м/с, в = 1.139 •Ю - ⁴м 2 / с, Bi = 194 > 100), значение коэффициента массо-отдачи равно в = 1.089 - 10 - ⁴ м² /с .

Для процесса диффузии жидких добавок внутрь экструдированных гранул по традиционной технологии в дражировочном барабанном аппарате были получены значения коэффициента диффузии жидких добавок D т = 4.78 • 10 - ⁴м² / с, а с применением вакуумной обработки увеличилось до D _т = 6.112 - 10 - ⁴ м² /с .

Затем, используя решение (9), определим профиль распределения расчетных значений концентраций жидких добавок по радиусу экструдированных гранул (рисунок 1).

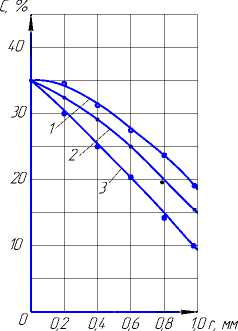
Рисунок 1. График изменения концентрации жидких добавок от глубины проникновения внутрь экструдированных гранул при различных значениях величины разряжении в рабочей камере вакуумного напылителя Р , МПа: 1 – 0.02; 2 – 0.03; 3 – 0.04

Figure 1. Graph of liquid additives concentration changes versus the depth of penetration into the extruded pellets at different values of the vacuum in the working chamber of the vacuum sprayer P, MPa: 1 – 0.02; 2 – 0.03; 3 – 0.04

post@vestnik-vsuet.ru

Сравнение расчетных кривых и экспериментальных данных показывает хорошую сходимость: среднеквадратичное отклонение не превышало 14.3%.

Таким образом, использование вакуумного напыления жидких добавок и их последующая диффузия внутрь экструдированных гранул позволяет не только увеличить на 30–35% коэффициент диффузии, но и добиться более равномерного распределения жидких добавок внутри гранул (рисунок 1).

Заключение

Для математического описания процесса диффузии жидких добавок внутрь капиллярнопористых экструдированных гранул использовано решение уравнения нестационарной молекулярной для тел, которое при постоянстве концентрации жидких добавок на поверхности гранул имеет вид быстросходящегося ряда. Было получено выражение для определения продолжительности процесса диффузии. Сравнение расчетных кривых и экспериментальных данных показало, что среднеквадратичное отклонение не превышало 14.3%.