Математическое моделирование процесса гомогенной конденсации оксида алюминия в смеси с углекислым газом

Исследованию горения алюминия и образования его оксида посвящены работы многих авторов [1–5]. Моделирование конденсации оксида алюминия Al ₂ O ₃ всегда осложнялось тем, что в газообразном состоянии этого вещества не существует [6]. По этой же причине осложнены расчеты получения его кластеров, т.к. распространенные модели конденсации [7, 8] подразумевают конденсацию вещества без изменения химической формулы. Алюминий широко используется в ракетной технике, как часть состава ракетных топлив. Расчеты, связанные с получением состава продуктов сгорания, включают в себя необходимость получения данных по образованию его окислов в движущемся потоке, которые, в свою очередь, осложнены индивидуальными свойствами оксида алюминия. Ранее в работах [9–11] была предложена модель для расчета движущегося насыщенного газа с учетом гомогенной конденсации в соплах, но в виду особенности оксида алюминия применить по аналогии эту модель не представляется возможным. В представленной работе предложена переработанная методика расчета движения насыщенного газа по соплу с учетом агломератов, специально адаптированная для оксида алюминия в среде аргона.

1.    Модель образования кластера Al2O3

Ранее в работах [9, 10] была предложена модель для расчета движущегося насыщенного газа с учетом гомогенной конденсации в сверхзвуковых соплах. Данная работа основывается на этой модели с некоторыми доработками, касающиеся особенностей образования оксида алюминия и состава продуктов сгорания. Расчеты условно разделены на два этапа, на первом вычисляется гомогенный состав продуктов сгорания с учетом образующихся кластеров оксида алюминия, на втором с учетом их спонтанной конденсации.

Газообразные продукты горения конденсируются в макроскопические капли жидкого оксида алюминия, получение термодинамических параметров таких кластеров осложнено тем, что A1 2 O 3 в газовой фазе экспериментально не наблюдается, что заставляет менять существующую численную модель гомогенной конденсации. Образование кластеров оксида происходит за счет реакции слипания различных его газообразных окислов, в связи с этим для точного определения термодинамических параметров кластера оксида алюминия необходимо знать – за счет которых именно веществ происходит его образование, а так же состав насыщенной смеси в равновесном и неравновесном состоянии для определения потока массы тех компонентов, которые обеспечивают рост зародышей оксида алюминия. Газообразный оксид алюминия при этом можно считать промежуточным продуктом с коротким периодом существования.

Составляем модель расчета неравновесного состава продуктов сгорания [9], где помимо основных оксидов и окислов, получающихся при сгорании алюминия в среде углекислого газа, присутствуют так же кластеры A1 2 O 3 . Общая система уравнения реакции будет выглядеть как:

' Al + O ^ AlO, 2Al + O ^ AI 2 O, 2Al + 2O ^ Al ₂ O ₂ , Al + 2O ^ AlO 2 , 2O ^ O 2 ,

< C + O ^ CO,                                (1)

C + 2O ^ CO 2 ,

4 (2Al + 3O) ^ 4Al 2 O 3 , 7(2Al + 3O) ^ 4Al 2 O 3 , • ••

n(2Al + 3O) ^ nAl2O3, где последние 3 строки - это кластеры размера 4, 7 и до n-го размера, т.е размерный ряд кластеров представлен по аналогии с рядом Фибоначчи, начиная с 4-го размера. Подробно об этом было изложено в работе [9]. Малые агломераты в расчете не учитываются, что позволяет избежать необходимость иметь начальные данные по термодинамическим параметрам субокислов алюминия в газовой фазе, т.к. крупные кластеры рассчитываются по капельной модели [10]. Данные, полученные ранее, показывают, что вклад малых агломератов очень мал, а сверхкритическими кластерами для начала момента спонтанной конденсации являются кластеры размеров от 10 и более. Это все позволило исключить малые агломераты из расчетов [11].

Далее, составляем модель расчета равновесного состава продуктов сгорания, где термодинамические свойства индивидуальных веществ взяты из справочника [13]. Наличие кластеров не учитываются, а образующиеся молекулы оксида алюминия представлены сразу k-фазой. В алгоритме расчетов k-фаза берется как большая молекула, состоящая из 1000 атомов Al2 O3.

Для системы (1) применяем метод расчета равновесного состава смеси [9,12]. Численный эксперимент был проведен для конического сопла с тангенсом угла полураствора 0,1 и с длиной сверхзвуковой части равной 15 см. Соотношение продуктов сгорания алюминия и углекислого газа 1:1. Температура в критике сопла 4100 К, плотность смеси 0,5 кг/м ³ . Моментом начала спонтанной конденсации выбрано число сверхкритических кластеров в количестве 10 ¹⁵ в 1/м ³ , что для данного сопла наступает при температуре 3987 К, скорость образования сверхкритического кластера 1, 02 · 10 ²² зародышей в секунду, состав продуктов сгорания в этом случае представлен парциальными давлениями веществ в таблице:

Таблица

Вещество	Начало конденсации не равновесной	Начало конденсации равновесной	∆P
AlO	0,666	0,195	0,471
AlO 2	0,023	0,005	0,018
Al 2 O	0,275	0,032	0,243
O 2	0,675	0,396	0,279
Al 2 O 2	0,049	0,004	0,045
O	1,184	0,875	0,309
CO	1,439	1,495	- 0,056
CO 2	0,245	0,189	0,056
ΣP	4,67	3,19

Конденсация оксида алюминия в присутствии CO ₂ идет почти так же, как и в случае чистого кислорода. В обзорной статье [4] представлены основные виды реакций, из которых происходит образование кластеров. Основываясь на результатах этих авторов, а так же анализируя разности парциальных давлений в равновесном и неравновесном состояниях (последний столбец таблицы), делаем вывод, что основной поток массы, для образования кластеров Al ₂ O ₃ , а так же их роста будет осуществляться за счет 4-х реакций, которые будут вносить наиболее ощутимый вклад:

2AlO + O ↔ Al 2 O 3 ,

Al 2 O + O 2 ↔ Al 2 O 3 , 2AlO + CO 2 ↔ Al 2 O 3 + CO,

Al 2 O + 2CO 2 ↔ Al 2 O 3 + 2CO.

Разница в парциальных давлениях остальных компонентов не значительна, следовательно ощутимого роста массы полного оксида за счет их слияния не будет, поэтому далее в расчетах этими реакциями можно пренебречь.

2.    Расчет потока насыщенного газа по соплу с учетом агломератов оксида алюминия

Первый этап численной модели расчета гомогенной конденсации заканчивается моментом образования сверхкритического кластера в достаточном количестве, то есть при N = 10i5 м-3. Второй этап, образование новых агломератов оксида не происходит, идет спонтанный рост существующих за счет реакций (3). Результатом двух последних реакций является выделение побочного продукта -CO.

Первый этап включает в себя следующие уравнения:

– для числа (концентрации) сверхкритических кластеров:

dN

IT = g ’

– для массы сверхкритических кластеров:

dm

If = 0,

– для плотности газовой фазы:

dρ dt

M ²

M ²

- 1

·

ρ _· dF _{· V}

F ( x ) dx

-

I g · g cr · m 1 ,

– для температуры потока:

dT _ (k - 1) M ²

It =    M ² - 1

·

dF

F (x) fc ^ V ⁺ I g • g cr • m ¹ •

T

·

^H cond ρ 0 C V

·

sv

, z

– для скорости потока:

dV dt

M ²

V

-

^dF · V,

1 F ( x ) dx

·

·

– для текущей координаты:

dx

dt = ’

– для изменения массовой доли оксидов:

dG

» = 0'

где I g = K k • n _{g -i} • n g -2 — скорость образования сверхкритических кластеров [10,11], n g - 1 и n g - 2 – концентрации докритических кластеров, при коагуляции которых образуется сверхкритический кластер, K k – постоянная скорости коагуляции, g cr – число частиц в сверхкритическом кластере, m – масса кластера, которая после образования достаточного количества сверхкритических кластеров и при начале их роста может быть принята равной массе сверхкритического кластера m o = m _i • g cr , или с учетом постепенного накопления сверхкритических кластеров возможно разных размеров, например, при быстром охлаждении (течения в сверхзвуковых соплах) - m o = Р N^ ⁰ , m 1 = ₁oo¹g 1 n _a — масса моночастицы газа, кг, ^ 1 - мольная масса моногаза, г/моль.

Второй этап включает в себя следующие уравнения:

– для числа (концентрации) сверхкритических кластеров:

dN

IT = 0'

– для массы сверхкритических кластеров (рост в условиях свободномолекулярного режима [8]):

dm dt n cr

+

p 1 - p 1s

/ 2п -R0- T µ 1_1

+

p 1 - p 1s

/ 2п -R0- T

µ 1_2

+

p 2

-

2^

p 2s

+

µ 2_1

p 2 - p 2s

.^ -R0- T

µ 2_2

, (11)

p 3 - p 3s

/ 2п -R0- T µ 3_1

+

p 3 - p 3s

/ 2п -R0- T

µ 3_2

+

p 4

-

p 4s

/ 2n -R0- T µ 4_1

p 4 - p 4s

/ 2п -R0- T

µ 4_2

Г cr = Г 1 •

3 3 _· m 4 π  m 1 ^,

– для плотности газовой фазы:

dp     M ²     p dF v n dm

dt M ² — 1 F (x) dx           dt ,

– для температуры потока:

dT = - (k — 1) M ² ^ T dF V + (dm AH c_Ond dt M ² — 1 F (x) dx         dt p ₀ CV ¹

– для изменения массовой доли оксидов:

dG   1 dm dt    ρ0 dt , где в уравнении массы (9) p1 и p1s – значения парциальных давлений неравновесного и равновесного составов того вещества из продуктов 1-й реакции (3), чье изменение в давлении окажется наименьшим, как определено в первом разделе; аналогично для продуктов 2, 3 и 4-й реакций (1.3); µ1_1 и µ1_2 – мольные массы продуктов 1-й реакции (3), µ2_1 и µ2_2 – мольные массы продуктов 2-й реакции соответственно (3), для 3 и 4-й реакций мольные массы компонентов, которые образуют оксид алюминия, т.е без учета мольной массы CO. Уравнения для скорости (5) и текущей координаты сопла (6) остаются неизменными. Во всех уравнениях F(x) - площадь поперечного сечения сверхкритической части сопла (для конического сопла представляет собой линейную функцию от x). В связи с тем что образование агломератов оксида алюминия приводит к уменьшению массовой доли оксидов относительно углекислого газа, то на каждом шаге на обоих этапах помимо пересчета равновесного и неравновесного составов, необходимо еще и учитывать изменение массовой доли оксидов, в связи с чем и вводится в систему уравнение (12).

Обсуждение результатов

Проведен ряд численных расчетов по предложенной модели. На рис. 1 представлены результаты по температуре и давлению потока по длине сопла, а так же радиусу критического кластера. Из графиков видно, что характерное для сверхзвукового сопла падение температуры потока нарушается в момент начала спонтанной конденсации оксида (3987 К), наблюдается резкий скачок температуры, который вполне объясним выделением тепла при переходе вещества от газовой фазы к жидкой. Рост температуры прекращается в момент, когда замедляется рост размера капель конденсата. Схожая картина наблюдается не только с температурой, но и с давлением. На рис. 1 четко наблюдается отклонение давления в момент начала роста капель.

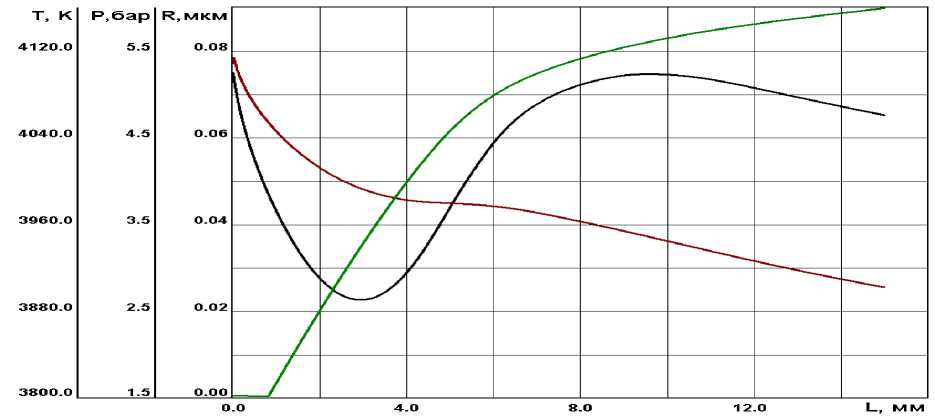
Рис. 1 . Температура, давление и радиус частиц оксида алюминия

В [1, 3] отмечается, что оксид алюминия, образующийся из газовой фазе, имеет субмикронный размер, а согласно полученным расчетным значениям (см. рис. 2) средний радиус образовавшейся капли, после момента спонтанной конденсации, достигает размеров порядка 0, 1 мкм. Из рис. 3 видно, что с ростом частиц оксида алюминия парциальные давления субокислов алюминия приближаются к своим равновесным значениям.

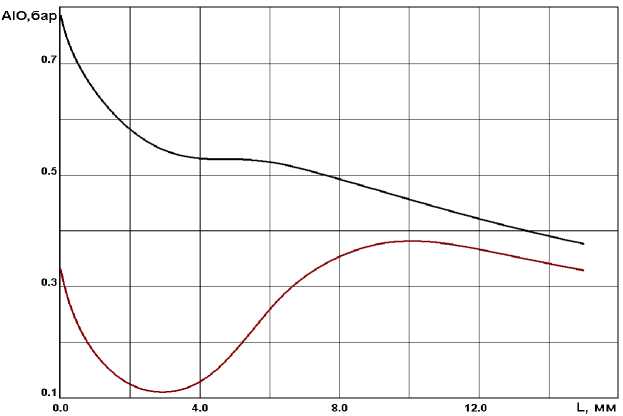
Рис. 2 . Парциальные давления AlO (равновесное и неравновесное)

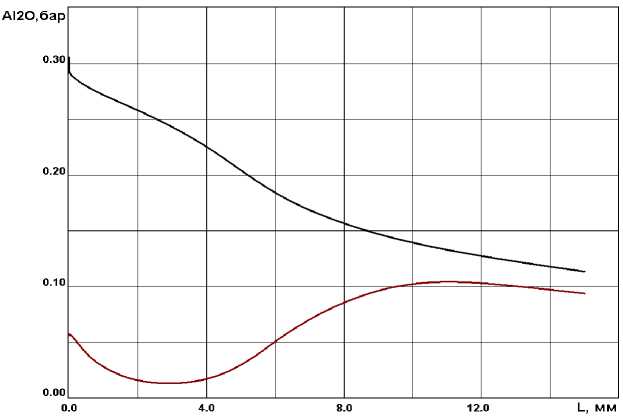
Рис. 3 . Парциальные давления Al 2 O (равновесное и неравновесное)

Публикация подготовлена в рамках работ по проекту 13.06.01/18КМА, реализуемому на основании Приказа ректора ИжГТУ имени М.Т. Калашникова от 29 декабря 2018 г. № 1493.