Математическое моделирование процесса очистки загрязненной тяжелыми металлами почвы с помощью биосурфактанта

Тяжелые металлы (никель, молибден, кадмий, цинк, свинец, ртуть), попадающие в окружающую среду в результате производственной деятельности человека, являются опасными загрязнителями биосферы. Они попадают в природную среду различными промышленными и бытовыми способами: в результате обработки металлов, изготовления металлоконструкций, производства краски, удобрений, вывоза отходов, сжигания топлива и т. д. [10, 11]. Находясь преимущественно в рассеянном состоянии, тяжелые металлы могут образовывать локальные аккумуляции в почве, где их концентрация в сотни и тысячи раз превышает среднепланетарные уровни. Например, более 40% нефтезагрязненных почв содержат высокие концентрации тяжелых металлов [4].

Няшин Юрий Иванович, д.т.н., профессор, завкафедрой теоретической механики, Пермь

Следует отметить, что тяжелые металлы сравнительно быстро накапливаются в почве и крайне медленно из нее выводятся из-за высокой степени сорбции и комплексообразования с почвенными компонентами. Они способны также накапливаться в отдельных звеньях трофической цепи и, таким образом, попадать в организмы высших животных и человека, подавляя их метаболическую активность и отрицательно воздействуя на жизнедеятельность.

Известно [10], что биогенные поверхностно-активные вещества (биоПАВ, биосурфактанты) способствуют десорбции солей тяжелых металлов и их удалению из почвенной среды. Данный процесс обусловлен двумя механизмами: во-первых, снижением межфазного натяжения на границе раздела фаз жидкость–твердое вещество и, во-вторых, комплексообразованием ионов металла с молекулами биосурфактанта. При этом эффективность десорбции металлов зависит от типа почвы, характера и уровня загрязнения, показателя кислотности среды, а также природы и химического строения используемого биосурфактанта. Так, показано, что внесение рамнолипидного биосурфактанта, синтезируемого бактерией Pseudomonas aeruginosa , приводит к эффективному удалению солей кадмия и никеля из загрязненной почвы [11]. Однако следует отметить, что патогенность бактерии-продуцента существенно ограничивает возможность промышленного применения рамнолипидов. В этой связи актуально изучение металл-десорбирующих свойств биосурфактантов, продуцируемых непатогенными микроорганизмами. Важно отметить, что биосурфактанты могут связывать ионы тяжелых металлов, оставаясь подвижными в почвенных средах и увеличивая тем самым подвижность ионов.

В лаборатории алканотрофных микроорганизмов Института экологии и генетики микроорганизмов УрО РАН получены высокоактивные биосурфактанты, синтезируемые непатогенными актинобактериями рода Rhodococcus [4]. Полученные биосурфактанты с высокой нефтеэмульгирующей и нефтеотмывающей способностью успешно применяются в процессах биоремедиации загрязненных почвогрунтов [1]. Лабораторные исследования показали, что Rhodococcus -биосурфактант способствует эффективной десорбции нефтяных углеводородов [8] и солей тяжелых металлов [3] из загрязненной почвы.

Для подбора эффективных приемов и создания оптимальной схемы биоремедиации необходимо построение математических моделей, адекватно описывающих процесс очистки загрязненного почвогрунта от нефти и тяжелых металлов с помощью биосурфактанта. Ранее авторами [5, 9] построена согласующаяся с экспериментальными данными модель нефтеотмывания загрязненного почвогрунта под действием Rhodococcus -биосурфактанта. Построенная для случая проникновения биосурфактанта в нефтезагрязненной почве модель (одномерная модель фильтрации биосурфактанта в лабораторной почвенной колонке) применена для моделирования процессов фильтрации воды и биосурфактанта в почве, загрязненной солями тяжелых металлов [2].

В рамках данной работы моделируются процессы сорбции и десорбции солей тяжелых металлов почвой, с помощью модели рассчитывается количество десорбированной соли. Путем сопоставления экспериментальных данных с результатами, полученными с помощью теоретической модели, оценивается эффективность использования биосурфактанта в технологиях очистки почвы, загрязненной тяжелыми металлами.

Описание моделируемого процесса

Процессы сорбции и десорбции солей тяжелых металлов изучались в модельных почвенных колонках. Наблюдалась динамика извлечения солей никеля и молибдена из почвы под действием водной эмульсии Rhodococcus -биосурфактанта (4 г/л, штамм Rhodococcus ruber ИЭГМ 231), синтетического биосурфактанта Tween 80 и дистиллированной воды.

Загрязненная солями тяжелых металлов модельная почва находилась в стеклянных колонках (рис. 1). Выше нулевой отметки находилась жидкость, ниже нулевой отметки – загрязненная почва и проникшая в почву жидкость; поверхность почвы отвечает координате x = 0.

Параметры колонок: диаметр d = 28 мм, высота слоя почвы L = 410 мм. Состав почвы (в объемных долях): песок – 50, глина – 30, торф – 20.

Количественное определение ионов никеля и молибдена, десорбированных из почвы в водную фазу, проводилось с помощью спектрофотометра диметилглиоксимным и роданидным методом соответственно. Эффективность процесса десорбции с течением времени t выражалась в массовой доле ц ( t ) десорбированной соли от общего начального количества сорбированной соли. В табл. 1 приведены максимально достижимые (за 24 ч) значения ц * величины ц . Полученные результаты свидетельствуют о высокой эффективности применения Rhodococcus -биосурфактанта для удаления солей исследуемых тяжелых металлов из почвы, что указывает на перспективность его использования в технологиях очистки загрязненных почв и грунтов.

Таблица 1

Экспериментальные результаты десорбции ионов никеля и молибдена из почвы

Металл	Эффективность десорбции µ *
	Rhodococcus -биосурфактант	Tween 80	Дистиллированная вода
Hикель	0,223	0,035	0,005
Молибден	0,217	0,032	0,003

Экспериментально также измерялась скорость течения жидкости через колонку. Она менялась со временем (первая порция жидкости протекала быстрее) и в среднем составляла V = 0,1 м/ч.

Описание математической модели

Математическая модель очистки почвы от солей тяжелых металлов основана на уравнениях материального баланса [7], описывающих десорбцию тяжелых металлов от почвы и повторную сорбцию их к почве:

m ( x , t + dt ) = m ( x - Vdt , t ) + a n ( x , t ) dt - в m ( x , t ) dt ,                    (1)

n ( x , t + dt ) = n ( x , t ) - a n ( x , t ) dt + в m ( x , t ) dt ,                         (2)

где x – координата, отсчитываемая вдоль колонки (см. рис. 1), t – время, m – концентрация десорбированной соли, n – концентрация сорбированной соли, a - коэффициент сорбции, в — коэффициент повторной сорбции, V - скорость течения жидкости в загрязненной почве. Из (1, 2) с учетом начальных условий ( n ₀ – начальная концентрация соли в почве) получаем основную начально-краевую задачу для уравнений (переноса) в частных производных:

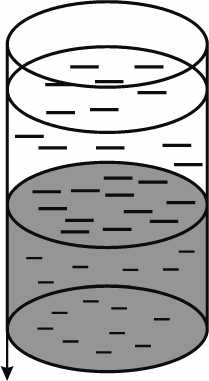
Рис. 1. Схематическое изображение почвенной колонки

mt + Vmx = a n -в m, nt =-аn + вm, x > 0, t > 0, •nit=0 = n 0, mt =0 = 0, ml „ = 0.

• I    x = 0

Задача (3) решалась методом преобразования Лапласа [6]. После изображениям M(x, p), N(x, p) функций m(x, t), n(x, t) из (3) получим pM + VM x = aN-вM, x > 0,

• < pN - n ₀ = -a N + в M ,

. M i x = 0 = 0.

Если не учитывать повторную сорбцию (в = 0), то из (4) находим перехода к

a n ₀

M ( x , p ) = —----- -( 1 - exp( - px V ) ) , N ( x , p )

p ( p + a )

ⁿ 0

p + a ,

откуда m (x, t) = <

n ₀

( 1 - exp ( -a t ) ) , 0 <  t

< —

V ’

n ₀

exp( -a t ) ( exp ( a x/V ) - 1 ) ,

t

> —

V ’

n ( x , t ) = n ₀ exp( -a t ).

В общем случае (в ^ 0) из (4) находим an 0

M ( x , p ) =--------—

p (p + a + в)

(

1 - exp

v

^ p(p + a + в)x

^^^^^H

N ( x , p ) =

ⁿ 0

p (p + a + в)

p + в-v

V

ав

p + a

exp

V ( p + a )

,

f p(p + a + в)x ))

V    V (p + a) ))

.

Учитывая, что, во-первых, оригиналом для exp (к/p)/p является 10 (2 Jkt) (функция Бесселя мнимого аргумента), во-вторых, оригиналом для exp(-kp)F(p) является функция, равная f (t - к) при t > к и нулю при t < к, в-третьих, оригиналом для произведения изображений является свертка оригиналов [6], из (5, 6) находим aлп .                      аПа m (x, t) =-----(1 - exp( - (а + В) t))--—exp(-B x / V) x

а + в               а+в

' 0, 0 <  t <  xV , t ^- x/V                     ___________ (7)

x A

J exp(-aт)10 (27авxт/V )(а + вexp (-(а + в)(t - x(V -т)))dт, t > x/V,

. 0

n ( x , t ) = n 0

1 ——+ ( а + в

_а               ^ аВ n ₀

----  exp^{( - ( а + в )} t )---^exP^{( -в} x / V ) ^x а+в           а+в

'0, 0 < t < x/V, x A

t - x/V

J exp( -aт ) 1 ₀ ( 2 а в x т/ V ) ( 1 - exp ( - ( а + в ) ( t - x/V -т ) ) ) d т , t >  x/V .

. 0

Экспериментально измеряемая зависимость ц ( t ) выражается следующим соотношением:

V Ц * t ц ( t ) =----- m ( L , т ) d т ,

Ln 0 ₀

где Ц * = lim ц(t). Из (7) получаем t —^^

[ '0, 0 < t < L/V                      " а V ц* Ц( t) = 7----^77 (а + в) L 1 - expCHa + p) t) t а+в t - x/V exp (-вL/V) J Ц(t, т) dт, t > L/V 0                                 _ , (8) где

Ц(t, т) = exp(-aт)10 (27авLт/V) а(t - L/V -т) + а+^[1 - exp (-(а + в) (t - L/V -т))] .

На рис. 2 приведены теоретические и экспериментальные зависимости ц ( t ). При этом величина ц * бралась из табл. 1, а величины а , в , V находились методом наименьших квадратов. Полученные значения приведены в табл. 2. Сопоставление теоретических и экспериментальных зависимостей (рис. 2) свидетельствует о том, что построенная теория удовлетворительно описывает процесс десорбции солей тяжелых металлов от почвы, что подтверждает адекватность разработанной математической модели. Имеется также удовлетворительное совпадение вычисленных величин V и экспериментально измеренной величины V = 0,1 м/ч.

Дальнейшее развитие модели может состоять в учете переменной скорости V течения жидкости. Кроме того, следует заметить, что при «продолжении» экспериментальных точек на рис. 2 к значению t = 0 они «не вполне стремятся» к значению ц = 0, что требует как качественного, так и количественного объяснения.

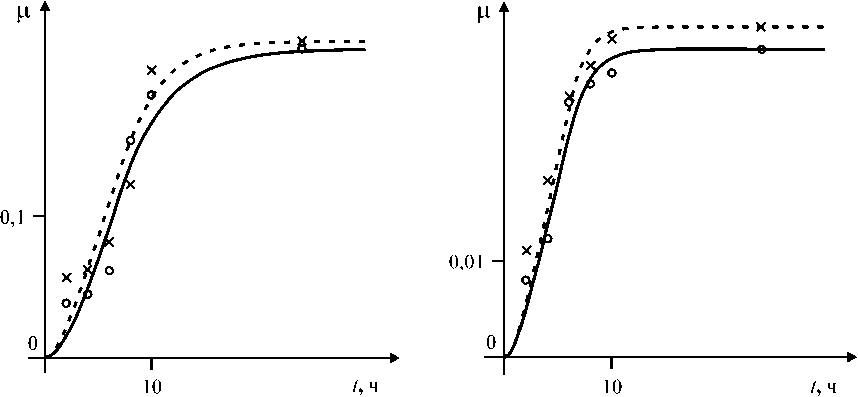
а

б

Рис. 2. Теоретическая (линия) и экспериментальная (точки) зависимости от времени массовой доли десорбированной соли: а – для Rhodococcus -биосурфактанта; б – для синтетического сурфактанта Tween 80. Сплошная линия и кружки – для солей молибдена, пунктирная линия и крестики – для солей никеля

Таблица 2

Значения констант моделирования, найденные при обработке экспериментальных данных

Константа	Rhodococcus -биосурфактант		Tween 80
	Никель	Молибден	Никель	Молибден
α, 1/ч	0,54	0,31	0,92	0,82
β, 1/ч	0,07	0,07	0,09	0,12
V , м/ч	0,071	0,071	0,083	0,083

Заключение

В настоящей работе представлены результаты экспериментального и теоретического исследования процессов сорбции и десорбции солей тяжелых металлов (никеля и молибдена) в почве под действием Rhodococcus -биосурфактанта. Построена математическая модель этих процессов. С помощью этой модели и на основании экспериментальных данных по динамике извлечения солей тяжелых металлов из почвы определены константы моделирования. Проведенное сравнение экспериментальных данных с результатами, полученными с помощью теоретической модели, свидетельствует об адекватности разработанной модели. Она является перспективной и допускает дальнейшее развитие.

Благодарности

Исследования поддержаны грантами Президента РФ для поддержки ведущих научных школ (НШ-64403.2010.4) и программами Президиума РАН «Молекулярная и клеточная биология», «Биоразнообразие».