Математическое моделирование процесса охлаждения заготовок из алюминиевых сплавов при термообработке

Термическая обработка заготовок из алюминиевых сплавов, широко используемых при производстве крупногабаритных маложестких деталей, заключается в проведении закалки и искусственного старения [1]. В процессе закалки происходит быстрое неравномерное охлаждение заготовки, которое формирует уровень температурных напряжений, превышающий предел текучести материала, что в свою очередь приводит к возникновению неравномерных пластических деформаций заготовки. При полном охлаждении заготовки до равномерной температуры по всему телу, неравномерные пластические деформации приводят к возникновению термических остаточных напряжений (ОН). Данные напряжения после механической обработки приводят к возникновению коробления деталей и их дорогостоящему браку. Следовательно, решение задач исследования процессов формирования остаточного напряженно-деформированного состояния (НДС) на основе математического моделирования является актуальной задачей.

На сегодняшний день, вопрос остаточных деформаций исследован на достаточно высоком уровне. Использование математических моделей, предложенных В.В. Абрамовым, И.А. Биргером, С.И. Ботвенко, Г. Бюлером, С.П.Гинкулом, Н.Н. Давиденковым, Ю.И. Замащиковым, С.И. Ивановым, С.К. Каргапольцевым, С.И. Ключниковым, В.Е. Койре, А.В. Лившицем, А.И. Промптовым, позволяет определять, как локальные, так и общие деформации маложестких деталей. При этом, узкое место исследований остаточного НДС, заключается в определении исходных данных для моделирования остаточных деформаций – определении термических остаточных напряжений. На сегодняшний день, указанные напряжения определяются либо разрушающими методами, что удорожает процесс производства, либо неразрушающими методами, использующими голографическую интерферометрию, электронную спекл-интерферометрию, рентгеновские и ультразвуковые методы измерения, которые имеют значительную (15-30%) погрешность измерения. Результаты работ, посвященных математическому моделированию остаточных напряжений, имеют узкую специфику. Примером являются работы Д.А. Мирзаева (моделирование ОН в поковках) [2], С.Л. Лебского (моделирование ОН после дробенаклепа) [3], С.А. Макеева (моделирование ОН в тонкостенном прокате) [4], И.Н. Кравченко (моделирование ОН при формировании плазменных покрытий) [5], С.И. Каратушин (моделирование ОН при цементации) [6] и т.д.. Это объясняется значительными отличиями физики протекающих процессов и нестационарностью параметров. На сегодняшний день наиболее перспективным, при моделировании нестационарных тепловых процессов является использование программных комплексов (MSC Nastran, Ansys и т.д.), реализующих численные методы расчета, которые являются мощными инструментами решения подобных прикладных задач. При этом, их использование в каждом конкретном случае так же связано с необходимостью трудоемкого определения специфических параметров процесса (таких как, коэффициент теплоотдачи, кривые ползучести материала в диапазоне температур обработки, распределение углерода по толщине при цементации и другие). В случае расчета нестационарного теплового поля в основу численных математических моделей положено уравнение теплопроводности (1) с соответствующими граничными условиями [2].

9Т 9 9Т 9 9Т 9 9Т рс — = -(X —) + -(X —) + -(X —) + Qw (х, у, z, t, T) = 0, (1) д t 9х 9х 9у ду дz дz где р - плотность, с - удельная теплоемкость, X - коэффициент теплопроводности, Qw (x, y, z, t, T) - мощность внутренних источников тепловыделения.

Применительно к моделированию процесса охлаждения в процессе закалки, вызывающей термические остаточные напряжения, необходимо отметить, что предлагаемые различными исследователями [7, 8, 9] работы не избавлены от основной проблемы расчета - определение температурозависимого коэффициента конвективной теплоотдачи, изменяющего в широких пределах (500-10000 Вт / м ² • К ), что тормозит дальнейшее изучение процесса формирования остаточных напряжений. Таким образом, задача формирования математической модели процесса с целью определения значений коэффициента теплоотдачи при различных условиях проведения термической обработки является актуальной.

Расчетно-экспериментальная модель процесса охлаждения заготовки при термической обработке

Для случая заготовки типа плиты, у которой ширина и длина значительно превышают толщину, справедливо перейти к одномерному уравнению теплопроводности:

dT дд2 Гп

р с— = Х—-, 0 < x < L. dt     ex2

Начальные и граничные условия описываются следующим образом:

д T

x = 0: X— = a1(T - T 1), t > 0, а1 > 0, дx x = L: X — = а 2( T - Te2), t > 0, а2 > 0, дx где X - коэффициент теплопроводности, Te1 и Te2 - температура внешней среды, T - начальная температура заготовки, а1 и а2 - коэффициент теплоотдачи.

Так как процесс закалки происходит при опускании заготовки вертикально, коэффициенты теплоотдачи а 1 и а ₂ и температура внешней среды T e ¹ и T e ² равны.

Коэффициент теплоотдачи, характеризующий процесс охлаждения заготовки в процессе закалки, зависит от значительного числа факторов, поэтому определить его значения расчетным способом представляется весьма трудной задачей, а справочные данные отсутствуют.

Учитывая вышесказанное, предложена расчетно-экспериментальная модель (6) нестационарного теплового поля, представляющая собой урав- нение Фурье-Кирхгофа с соответствующими начальными, граничными условиями и экспериментальными зависимостями изменения температуры в процессе закалки в различных сечениях исследуемой заготовки, позволяющая рассчитать коэффициент теплоотдачи и систему нестационар- ных тепловых полей, возникающих в процессе закалки.

д T „ д ² T рс— = Л—т д t      д x x

где 0 <  x <  L

начальные условия : при t = 0, 0 <  x <  L : T = T ₀

дT        _lx граничные условия: при x = 0: Л — = a1(T - T 1), где t > 0, a1 > 0, (6) дx при x = L: Л— = a2(T - Te2), где t > 0, a2 > 0, дx

T = f ,(x,t), где i = [1, 2, 3, 4, 5], t > 0, где Ti = fi (xi, t), где i = [1, 2, 3, 4, 5] - экспериментальные кривые охлаждения, характеризующие изменение температуры в сечениях исследуемого тела по толщине.

Расчет системы нестационарных тепловых полей осуществляется методом конечных разностей, на постоянной сетке, по неявной четырехточечной разностной схеме.

Определение коэффициента теплоотдачи, учитывая нелинейно изменяющиеся параметры, входящие в граничные условия, представляется весьма трудной задачей. Поэтому расчет температурнозависимого коэффициента теплоотдачи по кривым охлаждения осуществляется численным методом последовательного приближения в соответствии с разработанным алгоритмом (рисунок 1).

Расчет коэффициента теплоотдачи в конкретный момент времени закалки производится для условно стационарного состояния теплового поля и ведется на всем температурном интервале термообработки с заданной дискретностью. При этом, в расчетах используются экспериментально установленные значения температуры тела в сечениях заготовки на заданной глубине с использованием разработанного устройства [11].

Использование предложенной расчетно-экспериментальной модели и разработанного на ее основе алгоритма (рисунок 1) позволило определить значения температурозависимого коэффициента теплоотдачи. Для случая заготовки с габаритами 390*260*38 из сплава В95 a (t ) имеет вид, представленный на рисунке 2. Процесс изменения коэффициента теплоотдачи при термообработке протекает в четыре этапа, в соответствии с изменением режимов кипения закалочной среды.

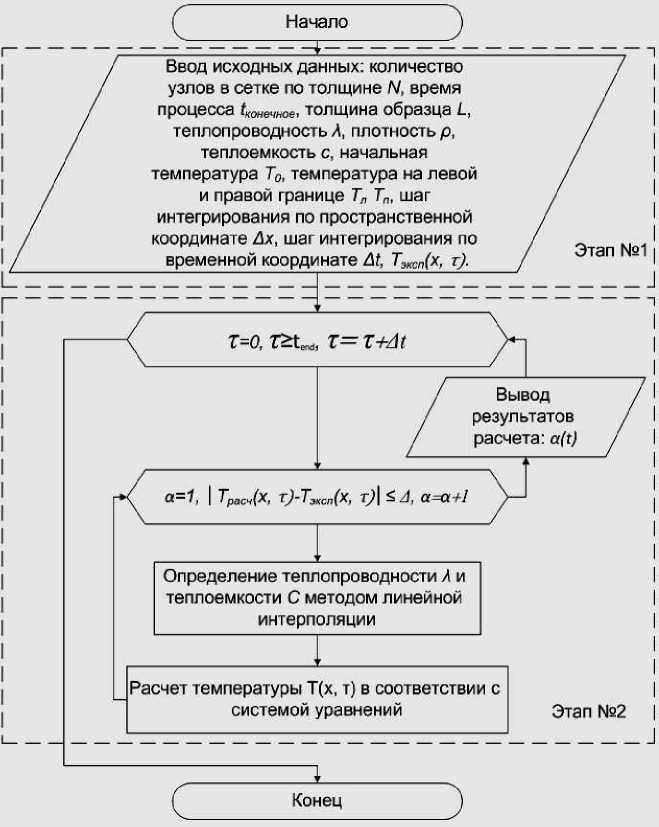
Рис. 1. Алгоритм определения коэффициента теплоотдачи по кривым охлаждения

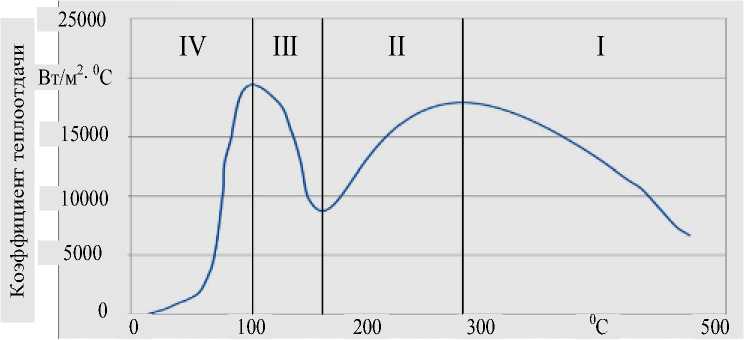
Температура поверхности охлаждаемой заготовки

Рис. 2. Температурно-зависимый коэффициент теплоотдачи

Заключение

Использование вышеприведенного коэффициента при расчете нестационарного теплового поля и термических остаточных напряжений дает расхождение с не превышающее 3,76 % с экспериментальными значениями, приведенными в работах [1, 12, 13], и может быть использовано в практических расчетах. Таким образом, впервые предложенные расчетноэкспериментальная модель и алгоритм расчета позволяют перейти от физических методов определения термических остаточных напряжений к расчету напряжений еще на этапе проектирования изделий и, соответственно, обеспечить снижение себестоимости продукции.