Математическое моделирование процесса принятия решения о состоянии стохастических систем

Стохастические системы, элементы которых могут иметь множество состояний и иерархически взаимодействовать между собой, с трудом поддаются моделированию, и их статистические модели, как правило, неизвестны. Описание таких систем осуществляется с использованием эвристически выбранных параметров состояния [6, 9, 11], которые будем называть признаками стохастической системы. Статистическое описание стохастических систем реализуется в пространстве эвристических признаков, а не состояний, что позволяет реализовать огромное сжатие информации.

Описание и прогнозирование состояния широчайшего класса технических, биотехнологических и экономических систем, которым присущи вероятностные связи между частями и иерархическая организация, возможны только на базе информационной модели их функционирования.

Материал и методы исследования

Пусть иерархически организованная система характеризуется N признаками, каждый из которых имеет n состояний с вероятностью появления Р i некоторого i -го состояния.

Под сложностью системы будем понимать число состояний её признаков, отличающихся друг от друга, которое характеризуется отношением N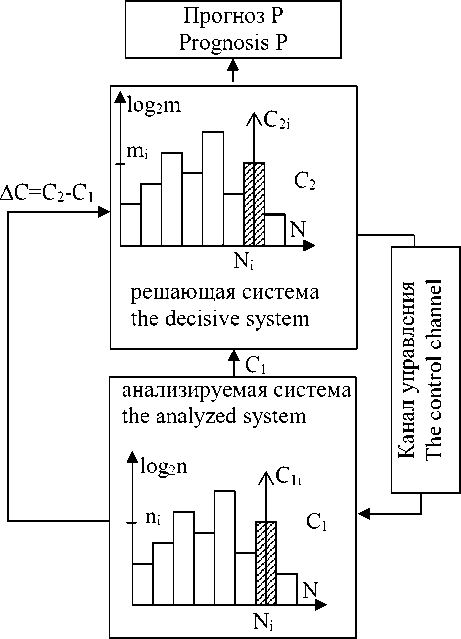![ П ( NP ) !, где П ( Np ) ^! число перестановок между состояниями признаков, не приводящее к изменению их функциональных отношений, а N! – полное число возможных перестановок. Учитывая требование аддитивности, сложность системы можно охарактеризовать выражением: n

П ( NP ) ^!

C = ^{— lo}g 2 i N !    .           ⁽1)

Согласно формуле Стирлинга для достаточно больших NP i :

n

C = — N £ Р , log₂ P ,          (2)

i = 1

Отсюда ясно, что сложность системы эквивалентна её информационной ёмкости. Максимальная ёмкость системы достигается, если все её состояния равновероятны, то есть Cm = Nlog2 n . Так как число градаций каждого признака может быть различным, то в общем случае полная информационная ёмкость сообщения, характеризующего сложную систему, определяется уравнением:

N

C 1 = £ ^log 2 n            ⁽³⁾

i = 1

Это сообщение поступает в решающую систему, содержащую априорную информацию в виде некоторой базы данных (рисунок 1).

Рисунок 1. Информационная модель иерархически организованной системы

Figure 1. Information model hierarchically organized system

Введём относительную неопределённость информации, получаемой решающей системой:

R = ^C- = 1

C

—

C 1

^, C ₂

N 2

где C 2 = £ log₂ m , - информационная ёмкость i = 1

базы данных решающей системы, N 2 – число информативных признаков системы.

Эта неопределённость затрудняет распознавание и классификацию полученной информации и может быть использована для управления анализируемой системой в канале обратной связи. Этот случай соответствует условию С1 < С2 и 0 < R < 1. Случай С1 > С2 соответствует прогнозированию поведения системы при недостатке или полном отсутствии априорной информации о ней, и –∞ < R < 0.

Случай R = 0 соответствует полному совпадению полученного сообщения с существующей базой данных, то есть система абсолютно предсказуема и управляема и может классифицироваться как детерминированная.

С учётом выражений (1) и (2) вероятность правильного предсказания состояния системы по некоторому N i признаку запишем следующим образом:

P i = n - R^               (5)

Проанализируем полученное соотношение. Если имеется абсолютно полная информация об анализируемой системе по каждому признаку (событию), то R = 0 и Р = 1 . Следовательно, система, несмотря на то что она может характеризоваться множеством признаков и состояний и быть очень сложной, является абсолютно предсказуемой, то есть детерминированной. То есть детерминизм – это предельный частный случай, когда возможно полное описание системы в выбранном пространстве признаков, которые являются определяющими в рамках решаемой задачи.

Если все состояния системы (события) равновероятны, то относительная неопределённость максимальна, то есть R i = 1 , P i = 1/n и n

^ P i = 1 - полная группа событий.

i = 1

Причём это характерно для абсолютно случайной системы, когда все состояния системы равновероятны и вероятность правильной классификации обратно пропорциональна их числу. Промежуточные случаи характеризуются некоторыми преимущественными состояниями системы и описываются различными статистическими распределениями.

Соотношение (5) является основой для построения классификационно-прогностической диаграммы состояния стохастических систем (рисунок 2). Для простых систем область существования детерминированных состояний 1 чрезвычайно мала. На рисунке 2 она ограничена кривыми для n = 1 и n = 2 и прямой R = 0,05 . Эти системы имеют практически одно состояние. К ним относится большинство технических систем, особенно механических.

• 2    – область существования однородных вероятностных систем. К ним относятся множество физических и химических систем, простейшие биологические и экономические системы.

• 3    – область существования сложных детерминированных систем. Она несколько больше области 1, но также достаточно мала. На рисунок 2 она ограничена кривыми для n = 2 и n = 16 и прямой R = 0,05 . Сюда можно отнести сложные технические системы, жесткоорганизованные кибернетические системы.

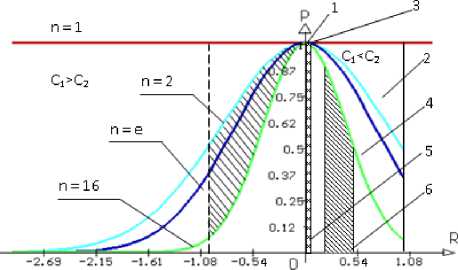
Рисунок 2.    Классификационно-прогностическая диаграмма

Figure 2. Classification-prognostic chart

• 4    – область существования сложных вероятностных систем, к которым можно

отнести иерархические системы искусственного интеллекта, а также экономические системы.

Наибольшее разнообразие для создания очень сложных детерминированных систем предоставляет область 5, что видно на примерах простейших биологических объектов – клеток, тканей, органов, которые, несмотря на огромную сложность, функционируют по строго заданной программе.

• 6    – область существования чрезвычайно

сложных вероятностных систем, иерархически гибко организованных, способных к саморазвитию и сложному поведению. К ним относится огромное разнообразие биологических видов, в том числе и человек. Это самая обширная область на диаграмме, что предполагает огромные возможности в создании самых разнообразных систем искусственного интеллекта. Здесь штриховкой выделена область существо- вания саморазвивающихся систем.

Величина 1 - R = C1 JC2 - относительная информационная ёмкость системы, характеризует качество прогноза. Введём коэффициент качества прогноза

K =

1 - R

R ,

Качество прогноза при K >  19 весьма высокое для детерминированных систем и ограничивается только ошибками измерений.

Для вероятностных систем качество прогноза удовлетворительное, если известен закон распределения их состояний ( 0,05 < R < 0,2, 4 <  K < 19 ). Саморазвивающиеся системы, обладающие свободой выбора, прогнозируютсясущественно хуже ( 0,2 < R < 0,5, 1 < K < 4 ). И, наконец, относительно абсолютно случайных систем можно лишь сказать, что все их состояния близки к равновероятным при R > 0,5 , когда коэффициент качества прогноза K <  1 . В этом случае никакой прогноз и управление системой невозможны.

Очевидно, что надёжное управление любой системой возможно в случае приближения информационной ёмкости управляемого сообщения (сигнала) С 1 к информационной ёмкости базы данных С 2 . Помехи в каналах управления и отказы отдельных элементов системы уменьшают информационную ёмкость сигнала управления, качество прогноза падает, и уменьшается вероятность правильного функционирования системы. Это приводит к отказам технических устройств, экономическим кризисам и болезням биологических объектов. Очевидно, для каждой системы есть своя пороговая величина Р , ниже которой нормальное функционирование системы становится невозможным и она погибает.

Левая часть диаграммы является прогностической, когда осуществляется анализ системы с использование априорной информации, заложенной в экспериментально накопленной базе данных. В этом случае С >  С 2 и значения R становятся отрицательными. Оптимальное прогнозирование системы опять реализуется в случае С 1 = С 2 , что подтверждается теорией распознавания образов [4]. Вероятность правильного принятия решения падает с уменьшением информационной ёмкости существующей базы данных и усложнением анализируемой системы.

Если информационная ёмкость сообщения вдвое превосходит таковую для базы данных, то есть С 1 ^С 2 = 2, то возможно лишь случайное предсказание состояния системы с вероятностью P = 1/ n . Следовательно, системы распознавания образов могут функционировать при условии 1 <  С 1 /С ₂ <  2 или - 1 <  R <  0.

Эта область ограничена на диаграмме пунктирной линией. Дальнейшее уменьшение информационной ёмкости базы данных С2 свидетельствует об отсутствии в ней адекватных алгоритмов анализа сообщения и вероятность правильного принятия решения стремится к нулю тем быстрее, чем сложнее анализируемая система. Аналогично при полном отсутствии информации о системе С1 = 0 и Р ^ 0 при |к| < 1.

Для вычисления вероятности правильного предсказания состояния системы введём её среднее значение в N -мерном пространстве признаков, с учётом выражения (5):

N         N        ₂ N J 1 - lo^g 2 n i 1

Е p i Е n - R i ')     Е n ¹ log² ™ i ^J2

p = — = 2=1-----= 2=1-------- (7)

NN  N

Здесь учтено, что размерности анализируемой системы признаков и решающей системы одинаковы, то есть определяются одной и той же экспериментальной базой данных.

Вследствие трудности построения строгих математических моделей технологических, биомедицинских и экономических систем получили своё развитие методы прогнозирования состояния на основе статистического анализа. Эвристическое описание таких систем осуществляется с использованием ряда признаков (параметров состояния, симптомов, экономических показателей), характеризующих макросостояние анализируемой системы [1–3, 5–8, 10].

Иерархическая организация таких систем и наличие блоков управления существенно ограничивает число их нормальных состояний. Поэтому дисперсия плотностей распределения признаков при нормальном состоянии анализируемых систем незначительна, что обеспечивает устойчивость их функционирования. Следовательно для описания нормального состояния анализируемых систем достаточно двух градаций каждого признака: среднего значения нормы m н и границы нормы х о (рисунок 3).

Выход за границу нормы приводит к аварийному функционированию системы со средним значением m а и значительной дисперсией признаков. Как правило, статистические распределения признаков в аварийном режиме функционирования неизвестны, а базы данных по этим признакам имеют малую мощность, так как существенные отклонения от нормального приводят к техногенным катастрофам, смертельным болезням биологических организмов и экономическим кризисам.

Для надёжного предсказания состояния анализируемой системы обычно измеряют несколько признаков N её состояния и осуществляют многофакторный анализ с исследованием различных методов [9–11].

При этом решаются две задачи: обнаружения, заключающаяся в оценке вероятности отклонения системы от нормального режима функционирования, и распознавания, заключающаяся в оценке степени отклонения от нормы. Первая задача сводится к построению решающей поверхности в многомерном пространстве признаков, разделяющей нормальную и аварийную области на базе принятого решающего правила. Вторая – к построению кластеров признаков, соответствующих принятым степеням отклонения от нормы и оценке положения измеренного многомерного вектора признаков.

Принципиальной трудностью, возникающей при решении указанных задач, является оценка минимально возможной мощности обучающей выборки и числа градаций признаков, обеспечивающих заданную вероятность решения задач обнаружения и распознавания в анализируемых системах.

Актуальность этой проблемы связана с бурным развитием современных средств измерений в различных областях науки и техники. Существующие датчики и системы контроля могут обеспечить чрезвычайно высокую точность измерений. При этом информационная ёмкость сигнала, поступающего в систему управления, может быть значительно большей, чем ёмкость обучающей выборки, что снижает вероятность правильного предсказания состояния системы [1].

Следовательно, возникает проблема оптимизации многофакторных измерений в анализируемых системах, то есть согласования относительно невысокой информационной мощности обучающей выборки и информационной ёмкости сигнала, обеспечиваемого современными средствами контроля, при сохранении заданной вероятности правильного предсказания состояния управляемой системы.

Задача обнаружения аварийного режима подобие классической – выбора одной из двух гипотез (рисунок 3) [4]. Если признак x попадает в область К 1 , то принимается гипотеза Н 1 – нормальное состояние; в область К 2 , то гипотеза Н 2 – аварийный режим. Однако порог обнаружения х о здесь определяется экспериментально.

Задача экспериментальной оценки порога х о является экспертной. Разделим область аварийного режима К 2 на три: лёгкое отклонение от нормы К 21 , среднее отклонение К 22 и тяжёлое – К 23 . Очевидно, что мощности обучающих выборок, соответствующих этим трём областям, будут различны и отличаются от мощности нормальной обучающей выборки.

Поэтому чрезвычайно высокая точность измерений вредна с этих позиций.

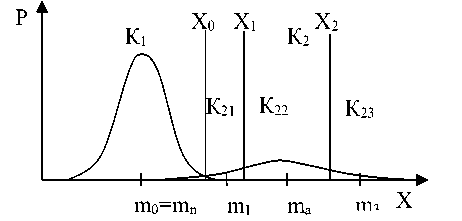
Рисунок 3. Классификационная диаграмма

Figure 3. Classification chart

Пороги Х 0 , Х 1 , Х 2 устанавливаются следующим образом. По обучающей выборке рассчитываются средние значения m 0 , m 1 , m 2 , т з и стандартная ошибка с о , c i , 0 2 , с з признаков по областям К 1 , К 21 , К 22 , К 23 . Порог:

X- —    , i = 0, 1, 2        (8)

^с >   ²

где А т - разность средних значений между соседними областями, с с > - отношение меньшей и большей стандартных ошибок соседних областей. Порог откладывается от среднего с меньшей ошибкой.

Для целей предотвращения аварийного режима необходимо весь динамический диапазон изменения признаков разбить на градации, а в пределах каждой градации производить усреднение сигнала. Наличие аварийной статистики позволяет уменьшить необходимое число градаций. Однако эвристический подход к установлению порога требует определённого запаса по числу градаций сигнала, область изменения которых в зависимости от мощности обучающей выборки можно задать следующим образом 8 < n < 20 .

Очевидно, что число градаций статистического ряда обучающей выборки, так же как и число градаций сигнала, должно быть связано с мощностью обучающей выборки. При слишком большом числе градаций частоты статистического ряда имеют незакономерные колебания. При слишком малом числе градаций описание очень грубое. Поэтому даже если информационная ёмкость обучающей выборки близка к информационной ёмкости сигнала, число градаций в пределах заданного выше диапазона должно сочетаться с объёмом выборки.

В [1] установлен минимально возможный объем статистического ряда:

L >  10 5 ,                 (9)

откуда следует, что 40 <  L <  10⁴ .

Следует отметить, что эвристические признаки, сложившиеся в практике, как правило, статистически зависимые [11], и подчёркивают те или иные специфические аспекты исследуемого процесса или явления. При проверке корреляционной связи между признаками и отборе статистически независимых, их число может быть существенно уменьшено.

Проведённые в [2, 3, 7, 8] экспериментальные исследования показали, что при описании системы с 8–30 признаками и мощностью обучающей выборки L от 40 до 120 методик, включающая в себя формализацию признаков на первом этапе, отбор с помощью корреляционного