Математическое моделирование процесса разрушения сплава АМГ2.5 в режиме много- и гигацикловой усталости

Элементы конструкций и детали машин в процессе эксплуатации испытывают циклические нагружения с различными амплитудами напряжений. В зависимости от величины приложенной нагрузки материал способен выдержать разное количество циклов до разрушения. Выделяют три типа усталостного разрушения. Первый тип — малоцикловая усталость (101–103 циклов), характеризуется амплитудами напряжений, превышающими предел текучести, реализацией макроскопических пластических деформаций и разрушением с образованием множественных трещин на поверхности эксплуатируемой детали. При многоцикловой усталости (104–107 циклов) — втором типе, амплитуды напряжений ниже или близки к пределу текучести, разрушение происходит за счёт инициирования единичной критической трещины на поверхности элемента конструкции. Третий тип — гигацикловая усталость (108–1010 циклов), наблюдается при напряжениях, существенно меньших предела текучести, и является следствием развития микропластических деформаций, локализованных в некоторых областях материала. Распространены случаи зарождения трещины под поверхностью, что делает данный тип разрушения наиболее опасным и проблемным для диагностики. Анализу закономерностей много- и гигациклового разрушения посвящён ряд работ [1–10]. Прикладная значимость и высокая стоимость оценки усталостного ресурса конструкций

послужили причинами создания лабораторных установок и методик для исследования механизмов разрушения в области сверхмногоцикловых режимов. Исследования проводятся, как правило, с использованием небольших образцов с концентраторами напряжений на высокочастотных (100 Гц) [8] и ультразвуковых (20 000 Гц) [10] машинах.

Цель лабораторного эксперимента заключается в обосновании моделей, описывающих стадийность развития повреждённости, инициирование и распространение трещин в повреждённой среде, что отражает специфику оценки ресурса в области сверхмногоцикловых нагружений по сравнению с традиционными подходами при мало- и многоцикловой усталости [11–17]. В [9–13] предложены обобщения моделей кинетики роста усталостных трещин (закона Пэриса) с учётом структурных факторов развития повреждённости. В то же время численное моделирование показало ограниченность существующих аналитических подходов и их адекватность лишь в определённом диапазоне напряжений [12–14]. Тем не менее, прямое численное моделирование разрушения в режиме гигацикловой усталости, а именно — решение краевой задачи даже для лабораторного образца, не говоря уже про реальную конструкцию, не представляется возможным из-за потребности в огромных вычислительных и временных ресурсах. Такое реализуемо лишь для малоцикловой усталости [15, 16]. Попытки решить краевую задачу при гигацикловых режимах сводятся к моделированию ситуации с уже образованной трещиной под поверхностью [12, 13]. При этом для процесса зарождения трещины используются аналитические оценки с помощью обобщённого закона Пэриса. Применимы также численно-аналитические подходы, согласно которым решается задача определения напряжённо-деформированного состояния при одном цикле, затем по найденным максимальным напряжениям аналитически рассчитывается число циклов до разрушения и прогнозируется разрушение деталей конструкций в режиме многоцикловой усталости [17]. Другой подход заключается в сведении пространственной постановки к обыкновенным дифференциальным уравнениям для представительных объёмов вблизи и вдали от свободной границы [14]. В последнем случае записываются определяющие соотношения для режимов много- и гигацикловой усталости с различными константами, что лишает модель универсальности.

Таким образом, актуальной задачей является обоснование модели, при помощи которой едиными уравнениями можно представить поведение материала при усталостном разрушении в широком диапазоне циклов нагружения (102–109). Цель настоящей работы состоит в построении определяющих соотношений для адекватного моделирования процесса циклического нагружения в широком диапазоне амплитуд напряжений. Задача рассмотрена для алюминиевого сплава АМг2.5 — материала, широко используемого в машиностроении.

2.    Математическая модель

Широкодиапазонные определяющие соотношения, связывающие кинетику повреждённости, обусловленную дефектами, с релаксационными свойствами материалов [18, 19] — суть математической модели, способной описывать деформационное поведение металлов и сплавов при циклическом нагружении.

Для учёта эволюции структуры материала вводятся два параметра: тензор-значный s и скалярозначный 5 :

s = s ( lb + bl ) /2 ,        5 = ( r]^ ) ³ .

Здесь: s — тензор микросдвигов; s — интенсивность сдвига; l — единичный вектор нормали к плоскости сдвига; b — единичный вектор в направлении сдвига; δ — масштабно-инвариантный структурный параметр; R — расстояние между дефектами; r — характерный размер зародышей дефектов.

Усреднение s по элементарному объёму даёт тензор плотности микросдвигов:

p = J sW ( s, l, b ) dV , где V — объём, W (s, l, b) — функция распределения ориентации и интенсивности сдвигов. По своему физическому смыслу p является деформацией, обусловленной дефектами.

Полная деформация скорости ( D ) состоит из трёх составляющих: пластической ( D ^pl ), упругой ( D ^e ) и обусловленной дефектами ( D ^p ):

D = D e + D pl + D ^p .

В случае малых деформаций d e = £ e, d pl = £p , d p = p , где £ e, £ p, p — упругая, пластическая и дефектная составляющие скорости деформации ε . Так как для рассматриваемых материалов (металлов и сплавов) параметр p всегда мал, то в дальнейшем вместо D p будет использовано обозначение p .

Из второго закона термодинамики следует, что диссипация энергии может быть представлена в виде:

pl д F       p д F

TS = о : D pl —---: D P —---5 > 0 , дp        д 5

где T — температура, S — скорость изменения энтропии, σ — тензор напряжений, F — неравновесная свободная энергия.

Согласно принципу Онзагера из (1) вытекают следующие соотношения:

—

° = 1х D p1 — 12 D P , (2) д F (3) ---= —12 D P1 + L D P , д p д F      " (4) —----= 14 § , д § где l , l , l , l , — положительные кинетические коэффициенты, в общем случае зависящие от параметров состояния и удовлетворяющие ограничению: у3 — 122 > 0 .

Соотношения (2)–(4) можно переписать в виде:

σ

D pl =Г i ° d

д F

-r2^7 •

-                d F p = Г 2 ° d —Г з ---, дp

5 =

д F

Г д 5

° — ° s ,

° s = “( ° : ^E ) ^E ,

где г = —³— , г = —²— , г =--¹— , г = — , E — единичный тензор, ° , и ° — девиаторная и

1113 — 12                11 13 — 12               1113 — 12

шаровая части тензора напряжений.

В уравнениях (5)–(7) используется следующее выражение для неравновесной свободной энергии:

• F     p     p                                  ₂ σ _d : p

  --- = --- —--- + c 1 P + c 2 ln ( c 3 + c 4 P + P )— ------- ,

F22δ1    2    3  42

m где F , c , …, c — константы потенциала (их значения приводятся в работе [18]), G — модуль сдвига, p = ^p : p . Напряжения определяются согласно изотропному закону Гука в скоростной формулировке:

° R = ^- ( D : E ) E + 2 G ( D — D ^p1 — p ) ,

где ( • ) R — производная Грина-Нагди [20, 21], - — первый параметр Ламе.

В случае необходимости учёта процессов диссипации энергии при неупругом деформировании система определяющих соотношений (5)–(9) дополняется уравнением теплопроводности:

P1 d F ■ О F

р cT = a A T + ° : D р —---: p —---5 , dp       д 5

где р — массовая плотность, c — удельная теплоёмкость, a — коэффициент теплопроводности, A(^) — оператор Лапласа.

Кинетические коэффициенты г. в общем случае зависят от параметров состояния и записываются как г = 1/ ( G т.) . Входящие сюда характерные времена релаксации т. можно представить в виде зависимостей [22]:

^т -

т exp I -

U . ( О , 8 , 8 , 8 p , 8 p , p , p , 5 , T ) ³

I , kT                I где k — постоянная Больцмана, и. (•) — характерная энергия активации.

В работе принимается гипотеза о том, что для исследуемых процессов времена релаксации выражаются так:

^т -

0      f U . S 0 - + ^U ( ^T ) - ^U 0 3

т. exp I ------------------------------- I

¹        I                   kT               I

( - = 1,2,3 ),

^т 4

т ₄

f exp I - l

^U 4 P 0 " — ^U 0 ³

kT    ;

k

U ( T ) = --- T

m

c

m + 1

Смысл данной гипотезы состоит в том, что физико-механические характеристики материала зависят от скорости деформации и температуры, а эволюция повреждённости при циклическом нагружении с малыми амплитудами напряжений обуславливается только параметром p , который в данном случае может интерпретироваться как скорость роста усталостной трещины, отнесённая к характерному масштабу задачи. В формулах (11)-(13) приняты обозначения: е0 = J(2/3)8 : 8 Л , где £с = 1 с-1 — обезразмеривающий множитель; и = kT , и. (- = 1, ..., 3 ) — константы, имеющие смысл характерных энергий преодоления барьеров, после которых активируются новые механизмы релаксации; po = ^p : p ^с ; tc , m — параметры, отвечающие за изменение механических характеристик в зависимости от температуры; n , n , n , n — константы, характеризующие скоростную чувствительность материала.

Выражение (11) можно представить в виде:

exP ( - ^и ( ^T )К ^kT )) exP ( ( U . S 0 ^- — ^и о )/ ( ^kT ) )

В предположении слабой скоростной чувствительности времён релаксации знаменатель дроби представим как разложение экспоненты в ряд в окрестности нуля с точностью до второго члена:

f и s ni - U 3        и s ni - U         и s n* U

U ε 0n kT ’

0          0                       0          0                    00

exp

|                  | « 1 +                 = 1 + l    kT    J         kT          kTkT в результате получим:

„ exp ( - и ( T )/( kT )) т ⁰ kT     f и ( T ) 3 т ^U      f U ( T ) )

т. = т. ----------------------= ——— exp |  ------ | = —— exp |   |

'     '     ( ^и^0k kT ))        ^u- ^s O '      i kT j ^s 0 '      i kT j

Аналогично поступим для выражения (12):

т

^т 4 exp I

—

^U 4 P О " - ^U 0 ³

^kT    J

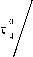
f U 4 p n exp I------

I

kT

^{- U 0} )-

f , + U 4 P n- U " | l        kT     J

т 4 kT

^U 4 P 0 "

U т4

.

n

P 0

Тогда кинетические коэффициенты примут следующий вид:

г = i

_ε0 ni

( i = 1, ..., 3 ),

^г 4

p

ⁿ 5

и                 (   )

GTi expl -          I к kT )

G т U

Введём обозначения, которые в дальнейшем позволят упростить запись уравнений:

.        f U ( T ) ^                  .         ( U ( T ) )                .         ( U ( T Й                 .

г, =г, 8n1 expl -------I ,    г 2 =г p , 8 n2 expl -------| ,    Г 3 = Г p 8 03 exp |          | , Г 4 = Г6 p^ , к kT )                      к kT )                     к kT к

0  = n₁ + n. , n = n₉ + n. .

£          1        2              p         2        3

Для замыкания системы определяющих уравнений необходимо ввести критерий разрушения. В рамках предложенной модели можно сформулировать несколько критериев, простейший из них

p : p ^ p_c ,

который хорошо зарекомендовал себя в задачах статического нагружения, а также в некоторых динамических задачах, когда не происходит смены нелинейной реакции материала на приложенную нагрузку ( 5 = const ). Другой вариант — температурный критерий разрушения:

т > т + (т - ^_ DRX ^{+ (} Пл

DRX

T DRX ) "          "   ,

⁸ DRX ^{+ 8} 0

согласно которому разрушение наступает после достижения температурой критического значения, которое тем меньше, чем больше скорость деформации. В (15) T — температура, при которой происходит существенное термическое разупрочнение материала, например — температура рекристаллизации; T — температура плавления; ε — характерная скорость деформации (обезразмеренная), после достижения которой начинаются процессы рекристаллизации при температурах ниже значения T . Данный критерий применим при динамическом нагружении в качестве основного (или как дополняющего (14)) при интенсивной локализации пластической деформации, приводящей к существенному разогреву.

Также можно ввести критерий на основе параметра структурного скейлинга:

5 ^ 0 .

Его смысл заключается в том, что объём, занимаемый в материале дефектами, стремится к 100%. Это может быть достигнуто за счёт уменьшения расстояния между дефектами или увеличения размера дефектов до бесконечности. Второй вариант невозможен, а первый имеет реальный физический смысл. В расчёте условие (16) не реализуемо из-за вычислительной неустойчивости, поэтому его можно заменить на следующее:

5 <  5 f ,

где 5f « 0,4 — критическое значение, после которого начинается лавинообразный рост дефектов и материал считается разрушенным. Естественно, значению 5 = 5 соответствует некоторое значение pc , поэтому можно считать критерии (17) и (14) эквивалентными. Однако (17) имеет ряд преимуществ: во-первых, обладает физическим смыслом, а во-вторых — большей универсальностью. Эволюция повреждённости в терминах δ определяется физико-механическими свойствами материала, а критическое значение δ одинаково для всех представителей конкретного класса, в то время как константу p необходимо определять для каждого материала. Кроме того, в терминах δ  адекватнее учитывается эволюция повреждённости при длительных циклических нагрузках, особенно с амплитудами напряжений, меньшими предела текучести.

3. Идентификация параметров модели

Идентификация параметров построенной модели (5)–(10) проводилась для представительного объёма материала:

Dpl

λ

-D + 2 G ( D - D^P -

^p ) ,

■         ■ n                         ⁽      )

p = e о ^p exp | ------- 11 ^r p , a - ^r

I ^kT )V

d F )

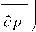
8 =

—

p : ^{s r} _§

d F d 8

F    p    p                             ₂    σ p

---- = ---- ^- --- ⁺ c 1 p ⁺ c 2 In ( c з ⁺ c 4 p ⁺ p ) ^- ---- ,

F 22δ2 G m

где D , σ , D pl , p — соответствующие компоненты тензоров D , σ , D pl , p . На первом этапе идентификации решалась задача минимизации невязки между экспериментальной и расчётной диаграммами деформирования. При этом определялись параметры г о, г ро , г р при фиксированных

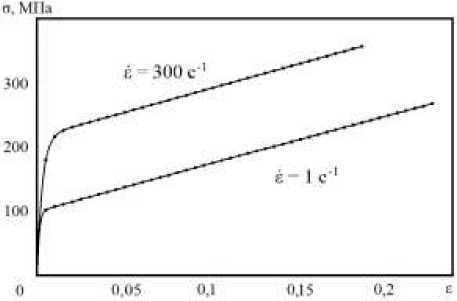
Рис. 1. Диаграммы деформирования при различных скоростях деформации: сплошная линия – расчёт, точки – эксперимент [8]

безразмерной  скорости деформации е₀ = 1

(статическое нагружение), 8 = const = 1,15 и т = о ° С . На втором этапе при известных значениях г , г , г минимизировалась О          p О          p невязка между экспериментальной и расчётной диаграммами деформирования при характерной скорости деформации 300 с-1. Устанавливались параметры пе и пр при 8 = const = 1,15 и т = о ° С .    На    этапах    использовались экспериментальные данные из статьи [8], в которой получены лишь пределы текучести, прочности и относительное удлинение при двух различных    скоростях    деформирования.

Для построения аналитических зависимостей по этим механическим характеристикам авторы

применяли методику, предложенную в [23]. Иллюстрация решения задач оптимизации представлена

на рисунке 1, где e — логарифмическая мера деформации, e = in ( 1 + J Ddt ) .

Для определения параметров T и m в общем случае необходимы диаграммы деформирования при фиксированной скорости деформации и различных температурах. Но такие данные не найдены в литературе, поэтому константы T и m идентифицировались путём минимизации разницы между статическими пределами прочности при температурах, равных 20, 100, 200 и 3 00 ° с . При этом фиксированными принимались скорость деформации е₀ = 1 и 8 = const = 1,15 . Результаты приведены в таблице 1, где под пределом прочности в расчёте понимается напряжение, соответствующее критической деформации.

Таблица 1. Предел прочности в эксперименте и расчёте при различных температурах

Температура, ° с	Предел прочности в эксперименте [24], МПа	Предел прочности в расчёте, МПа
20	280	282
100	265	263
200	191	193
300	103	103

Завершающий этап идентификации параметров модели заключался в определении значений г_§ и n_s , которые находились с использованием экспериментальных данных циклического нагружения [8] — двух характерных точек на кривой Вёлера: 37 500 циклов, 170 МПа и 1 850 000 циклов, 114 МПа. Параметры г_§ и n выбирались таким образом, чтобы при амплитуде нагружения 170 МПа материал выдерживал 37 500 циклов до разрушения, а при 114 МПа — 1 850 000 циклов соответственно. Частота нагружения при этом равнялась 100 Гц, как и в эксперименте.

Таким образом, полный набор констант для сплава АМг2.5 был следующим:

- константы, известные из литературы [24]: р = 2 67 о кг/м³, х = 41 ГПа, G = 27 ГПа, c = 900 Дж/К;

- установленные константы: го = 1170 (Па^с)-1, гра = 80 (Па-с)-1, гр = 5,60 (Па-с)-1, г5 = 4,89 (Па-с)-1, n = n = 0,84 , nR = 0,75 , T = 226 °C , m = 2 .

£           P                   "6           ,         c      C                          "

• 4.    Результаты численного моделирования

Численное исследование поведения реальной конструкции и даже лабораторного образца в режиме гигацикловой усталости не представляется возможным в связи с потребностью в огромных вычислительных и временных ресурсах. Поэтому вместо решения краевой задачи рассматривалась задача нагружения представительного объёма материала:

■     • np ^         /

P = 8 0 I г p „ ° (1 )-r p  I

(d

5 =

P n ^5г _§

d F a 5

^F p     p                   ,               2X ° ⁽ t ^{) P}

---- = ---- ^- --- + ^c 1 p + ^c 2 In ( ^c 3 + ^c 4 p + p )^- -------- ,

F 22δ2 G m

с условиями нагружения в виде приложенных циклических напряжений

° ( t ) = °_A sin ( 2 nu t )                                                     (26)

с амплитудой ° _д и частотой u , а также с начальными условиями

p [ = 0 = ⁰ ,        ⁵ 1 = 0 = ⁵ 0 = ^{1,1 5} .                                                 ⁽²⁷⁾

Уравнение (19) не принималось во внимание по причине того, что в режиме гигацикловой усталости макропластические деформации отсутствуют, и достаточно отслеживать эволюцию повреждённости. Температура испытаний, в соответствии с экспериментально реализованными режимами, предполагалась постоянной.

Условия нагружения (26) можно записать в терминах деформаций:

8 ( t ) = 8 ( ° _А ) sin ( 2 nu t ) ,

где 8 (°) — функция, переводящая напряжения в деформации, согласно нелинейной зависимости, полученной в ходе решения задачи (18)–(22). После дифференцирования (28) по времени получилось:

8 (t )= 8 (°д ) 2 nu sin (2 nu t) .(29)

Тогда для оценки скорости деформации как функции амплитуды и частоты нагружения стало возможным следующее выражение:

8 ( t ) = 8 ( ° А ) 2 nu sin ( 2 nu t ) < 8 ( ° A ) 2 nu = 8 08 c .(30)

Аналогично выглядела формула для оценки p :

P ( 1 ) = P ( ° A ) 2 nu sin ( 2 nu t ) < P ( ° A ) 2 nu = P 0 8 с .(31)

Результаты расчётов количества циклов до разрушения N в зависимости от амплитуды нагружения представлены на рисунке 2а. При построении S–N диаграммы (кривой Вёлера) (Рис. 2) использовался критерий разрушения (17). Моделирование в области многоцикловой усталости (104–107 циклов) проводилось с частотой u = 100 Гц подобно испытаниям в соответствующем эксперименте [8]. Расчёт в диапазоне гигацикловой усталости (10-1010 циклов) осуществлялся с частотой u = 20000 Гц, что отвечало режиму нагружения на ультразвуковых испытательных машинах [10]. При высоких амплитудах напряжений (180-280 МПа) частота выбиралась таким образом, чтобы выполнялось условие Nc /и ~ 103. Теоретическая S-N диаграмма хорошо согласуется с экспериментальным данным [8]. Эксперименты для сплава АМг2.5 в области мало- и гигацикловой усталости в литературе не найдены, однако сходимость к пределу прочности при Nc > о свидетельствует об адекватности участка 102-104 циклов.

Результаты моделирования позволили описать эффект дуальности кривой Вёлера, который заключается в изменении поведения материала при переходе от много - к гигацикловой усталости: на S - N диаграмме это выражается в изменении угла наклона кривой в логарифмических координатах (Рис. 2 а ). Напряжение, при котором происходит качественное изменение характера S - N кривой, близко к статическому пределу текучести. Однако, в силу скоростной чувствительности сплава АМг2.5, предел текучести при скоростях деформации, реализуемых в режиме гигацикловой усталости (~10² c^-1), выше чем 95 МПа. Поэтому трансформация кривой связана, по -видимому, с преодолением амплитудой нагружения предела пропорциональности.

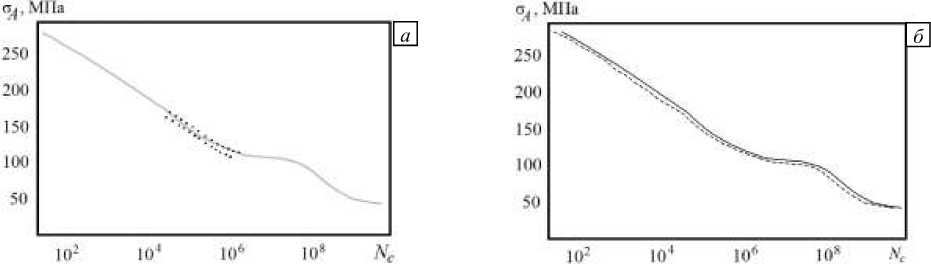
Рис. 2. Расчётная кривая Вёлера (сплошная линия) (а , б ), а также границы статистического разброса экспериментальных данных (точки) [8] ( а ) и S - N диаграмма после предварительного нагружения (пунктирная линия) ( б )

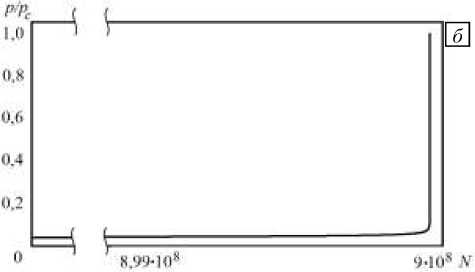
Характерная эволюция повреждённости для режимов много - и гигацикловой усталости изображена на рисунке 3. Для наглядности сопоставления результатов представлен последний миллион циклов (Рис. 3 б ). Видно, что переход к разрушению при больших амплитудах напряжений происходит более плавно, в то время как при малых амплитудах интенсивный лавинообразный рост трещины реализуется в кратчайшие сроки, что подтверждается данными других исследований [1-7, 10].

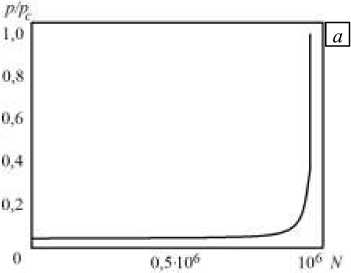
Рис. 3. Эволюция повреждённости в процессе усталостного нагружения при амплитуде напряжений 118 МПа и частоте 100 Гц ( а ), амплитуде напряжений 52 МПа и частоте 20 000 Гц ( б )

Проведено  моделирование  комбинированного (динамического и циклического) нагружения, распространенного в авиационных приложениях. Изменение структуры материала после предварительного динамического пластического деформирования учитывалось в задаче (23)-(27) заданием параметра 50 , характеризующего текущую «восприимчивость» материала к развитию дефектов. Для определения 50 решалась задача динамического нагружения (18)-(22). Зависимость 5 от величины предварительной деформации при различных скоростях деформации изображена на рисунке 4. Рассмотрен вариант предварительного  нагружения при с = 1000 c-1, с = 0,1 . Сравнение S-N кривых до и после предварительного нагружения можно видеть на рисунке 2б. Численный расчёт показал, что сплав АМг2.5 слабо чувствителен к предварительному динамическому нагружению при умеренных пластических деформациях и скоростях деформации ~103 c-1, что подтверждается экспериментальными результатами [8].

Проведено сравнение предложенной модели с аналитической моделью разрушения Коффина–Мэнсона (К-М-модель) [25], используемой в прикладных инженерных расчётах [17], которая имеет следующий вид:

ε _A

ε _c - ε _{- 1} ε _{- 1} + . N ^α N ^β cc

Здесь: ε — амплитуда приложенных деформаций; ε - ε — деформация, при которой материал будет разрушен за один цикл нагружения; ε — деформация, соответствующая напряжению σ , которое является пределом выносливости на определённой базе циклов (в случае многоцикловой усталости — это 10⁶, гигацикловой — 10⁹); α и β — подгоночные параметры. В случае, когда предел выносливости ниже или равен пределу пропорциональности, отвечающая ему деформация может быть вычислена как ε _{- 1} = σ_{- 1} IE , где E — модуль Юнга. Для сплава АМг2.5 параметры К–М-модели были следующими: ε = 0,22 , ε = 0,0014 , α = 0,39 , β= 0,09 . Результаты для сравнения изображены на рисунке 5.

К–М-модель определяет предел выносливости при β= 0 (в противном случае он отсутствует (Рис. 5)), хорошо описывает участок малоцикловой усталости, а также многоцикловую усталость материалов, имеющих предел выносливости, например, некоторых сталей. Однако она не отображает эффект дуальности кривой Вёлера, а также не учитывает эффекты скоростной чувствительности материала. Естественно, К–М-модель можно обобщить и учесть перечисленные эффекты, но это приведёт к существенному увеличению количества констант, которые уже не будут иметь явного физического смысла.

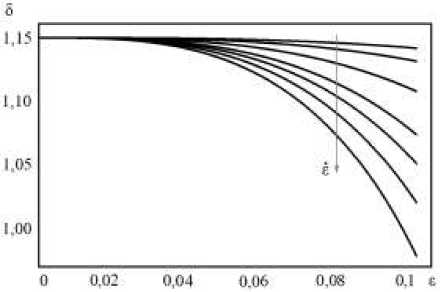
Рис. 4. Зависимость параметра δ от предварительной деформации при скоростях деформации ε , c^-1: 1, 100, 200, 500, 1000, 2000, 4000

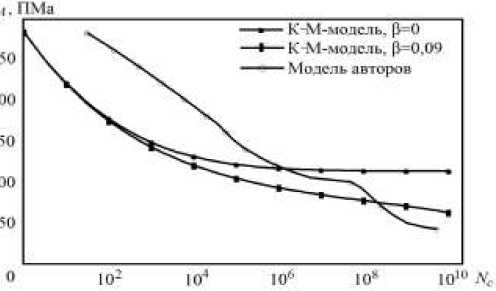
Рис. 5. К сравнению авторских результатов с расчётами по модели Коффина–Мэнсона

5.    Сравнение различных численных методов и математических пакетовдля решения задачи. Сходимость численного решения

В настоящей работе для численного решения поставленной задачи применены два математических пакета: Wolfram Mathematica (WM) и MatLab (ML). Проведено их сравнение на примере постановки при частоте 100 Гц и амплитуде напряжений 115 МПа. В Пакете WM использовалась функция «NDSolve» с заданной абсолютной точностью 10–6 и различными опциями «Method» В ML при тех же условиях нагружения с той же точностью прибегали к различным решателям (Табл. 2). В таблице показаны данные не всех возможных методов и решателей, а лишь тех, которые показали наиболее адекватные результаты. Другие методы и решатели либо демонстрировали неспособность разрешить рассматриваемую систему дифференциальных уравнений, либо имели время работы, на порядки большее приведённых в таблице (для всех пакетов и методов время счёта осреднено по десяти реализациям).

Из таблицы 2 видно, что WM даёт существенный выигрыш во времени. Однако это может быть связано с тем, что в данных пакетах по-разному определяется «абсолютная точность» численного решения. Но изменение в пакете ML точности на два порядка вверх/вниз не приводит к существенному изменению

Таблица 2. Время счёта в пакетах WM и ML для частоты 100 Гц, амплитуды напряжений 115 МПа с абсолютной точностью 10–6 при использовании различных численных методов решения и стандартных решателей

Метод Wolfram Mathematica Решатель MatLab Adams BDF Implicit Runge-Kutta Адамса– Башворта– Мултона (ode113) Рунге-Кутты 2-го и 4-го порядков (ode23) Рунге-Кутты 5-го порядка (ode45) N c 1456029 1455403 1457252 1453548 1458232 1463215 Время счёта, с 43,2 157,4 421,9 247 456 257 ни продолжительности вычислений, ни числа циклов до разрушения. Поэтому очевиден вывод о предпочтительности использования WM для решения рассматриваемой задачи. Также можно заключить, что наиболее предпочтительным методом численного интегрирования является метод Адамса и его модификации, что подтверждается расчётными данными (см. Табл. 2).

В таблице 3 приведены данные о сходимости численного решения. При частоте нагружения 100 Гц последние три цифры в значении N не достоверны как в эксперименте, так и в расчёте, поэтому точность выше 10^–7 не требуется. При амплитуде нагружения 115 МПа за 10 000 циклов значение параметра p изменяется на величину, имеющую порядок ~10^–6, вследствие этого точность ниже 10^–6 недопустима. При сравнении результатов расчётов, найденных с точностью 10^–7 и 10^–6, относительная погрешность составляет всего 0,1%, а время счёта отличается на 17%. Точность 10^–6 является оптимальной с точки зрения соотношения точность/скорость расчёта. Именно с таким уровнем точности получены результаты в области 10⁶–10¹⁰ циклов. При значении N <  10⁶ точность вычислений зависела от частоты нагружения и имела порядок 10^–7–10^–9.

Таблица 3. Сходимость численного решения, полученного методом Адамса, в пакете WM на примере нагружения при частоте 100 Гц и амплитуде напряжений 115 МПа

Точность	N c	Время счёта, с	Относительная погрешность, %
10 –4	1448446	25,7	–
10 –5	1455934	40,4	0,514
10 –6	1456029	46,1	0,007
10 –7	1457651	55,5	0,111
10 –8	1457313	74,4	0,023
10 –9	1457266	84,5	0,003
10 –10	1457251	104,2	0,001
10 –11	1457252	144,4	0,00007