Математическое моделирование процесса сушки модифицированного корма

Рассматривается сушильная установка для модифицированного корма с полной рециркуляцией воздуха (рисунок 1).

Рисунок 1 - Принципиальная схема сушильной установки

1 - сушильная камера; 2 – штуцер для подачи влажного сырья; 3 – штуцер для выхода влажного воздуха; 4 – перфорированные виброполки;

5 – штуцер для выхода высушенного сырья;

6 – штуцер для подачи воздуха в сушильную камеру; 7 – бункер для высушенного сырья; 8 – охладитель воздуха; 9 – влагоотделитель; 10 – циркуляционный вентилятор; 11 – калорифер

Влажный корм через штуцер 2 подается в сушильную камеру и двигается по вибрирующим полкам 4 в нижнюю часть сушильной камеры . Через штуцер 5 он выводится из аппарата и поступает в бункер-накопитель 7. Воздух подается через штуц ер 6, а выводится через штуц ер 3. В аппарате воздух преимуществ енно проходит через отверстия в полках перпендикулярно движущемуся слою сырья. Далее он поступает в охладитель 8, где охлаждается до температуры меньшей точки росы (рисунок 2).

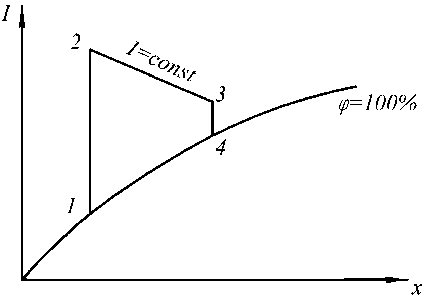
Рисунок 2 - I-x – диаграмма процесса сушки сырья: 1-2 – подогрев воздуха в калорифере 4; 2-3 – сушка сырья в сушильной камере 1; 3-4-1 – охлаждение воздуха в охладителе 8.

Капли влаги, образующ ейся в воздухе при его охлаждении , отделя ются во влагоотде-лителе 9, а воздух вентилятором 10 подается через калорифер 11 в сушильную камеру 1.

На рисунке 2 представлена I-x - диаграмма процесса сушки модифицированного корма.

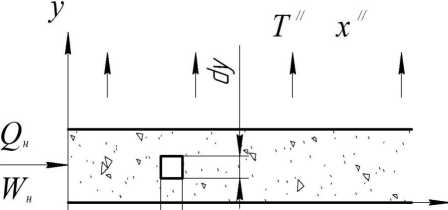
Рассмотрим процесс сушки, протекающий на отдельной вибрирующей полке сушильной камеры (рисунок 3).

GH dz vw Т х'

Рисунок 3 - Движение сред на полке

Влажное сырье в количестве G_H при вла-госодержании W н поступает на вибрирующую полку и перемещается по ней слева направо со средней скоростью u m. Воздух проходит через слой снизу вверх. Начальная и конечная температуры воздуха равны T и T / , влагосодержа-ния - X, X / .

Вибрация полок обеспечивает устойчивое движение сырья через аппарат, а также способствует существенному увеличению коэффициентов тепло- и массоотдачи и интенсификации процесса сушки.

При постановке задачи принимаем следующие допущения:

• -    высота слоя корма постоянна;

• -    средняя скорость направленного движения частиц корма постоянна;

• -    поля температуры и влагосодержания в частице корма однородны;

• -    частицы корма интенсивно перемешиваются в вертикальном направлении, обеспечивая постоянство температуры частиц по высоте слоя;

• -    тепло- и влагопроводность частиц сырья не оказывает существенного влияния на процесс сушки. Основными факторами, определяющими интенсивность сушки, являются процессы тепло- и массоотдачи на поверхности частиц сырья.

При известной средней скорости частиц расход корма определяется по формуле:

G T = v _T - b - h (1 - е ) p _T                  ⁽¹⁾

где u_T — средняя скорость движения частиц корма; b - ширина полки; h - высота слоя корма на полке; е - рабочая порозность слоя корма; р_т - плотность корма.

Удельная поверхность слоя корма определяется формулой:

f = n - F 4 ,                  ⁽²⁾

где n - количество частиц корма в 1 м³ слоя;

F₄ - площадь поверхности одной частицы.

6(1 - е ) n d ³

F₄ = n d ²,                (4)

где d - средний эквивалентный диаметр частиц корма.

С учетом (3), (4) из формулы (2) следует:

6(1 - е )

Выделим элемент dz-dy (рисунок 3) и составим для него уравнение теплового баланса:

^Своз • ^и воз • Р воз • ^dz • ^dT = « ^{( 0}- ^T ) • f • ^dz • dy , ⁽⁶⁾

где c„ - теплоемкость воздуха; и, - ско-воз                                              воз рость воздуха (вертикальная составляющая на свободное сечение камеры); рвоз - плотность воздуха; T - температура воздуха, К; а - коэффициент теплоотдачи от воздуха к поверхности частиц; 0 - температура частиц корма (зависит от z, но не зависит от у).

Разделив выражение (6) на dz^dy, получим:

dT =--- O f ---( 0_ т )        (7)

dy c - p -u воз воз воз

Начальные условия: T=T при у =0.

Разделяя переменные и интегрируя (7), получим:

T = 0 + ( T¹ -0 )exp I-- —-- у I ⁽⁸⁾

c - р -и воз воз воз

Температуру воздуха на выходе из слоя получаем из (8) подстановкой y=h :

T" =0 + ( T / -0 )exp

а - f - h c - р -и воз воз воз

Уравнение массоотдачи для элемента dz-dy:

Р воз • ^ивоз • dx ^dz =       ^{( P}nw - ^РП ) ^- f ^{- dz -} dy , ⁽¹⁰⁾

RПT где x - влагосодержание воздуха; в - коэффициент массоотдачи; Rn - газовая постоянная для пара (для водяного пара Rn=461 Дж/кгК); T - средняя абсолютная температура; РП - парциальное давление пара в воздухе;

P_n W - парциальное давление пара у поверхно

сти частиц.

Величину P_nw полагаем равной равно

Зaвисимость пapциaльного дaвления пара у поверхности частицы Pnw от абсолют

ной температуры частицы 0 определяется

весному давлению пара для температуры ча

стицы 0 . Величина влагосодержания х мо

соотношением [2]:

жет быть рассчитана по формуле [1] через

^PПW ^Р П • ^exp

r

—

давление Р_п :

х = 0,622

P Π

П — Рп ’

где П - давление в сушильной камере

( П ~10⁵ Па)

Полная Р _п <<П из (11) получим:

х = 0,622   ,           (12)

Π

Разделив уравнение (10) на dy-dz с учетом (12), получим:

dPΠ dy

№

0,622 Р воз -О воз

_р ™ ⁽ P nw ^Рп ) ⁽¹³⁾ ' R n ' T

Решение уравнения (13) при начальном условии Р_П(0)=Р П имеет вид:

^Рп ^Pnw + ^{( Р}П ^Pnw ^)exp |                 п т

( ^0,622 Р _6ОЗ "V^ • ^Rn • ^T

На выходе из слоя (y=h ):

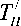
I

, (18)

где Т_Н / - температура насыщения пара для давления пара Р п/ .

Начальные условия для уравнения (17):

0 (0)= 0 н

Решение дифференциaльного урaвнения (17) при начальном условии (19) можно представить в неявном виде:

где

A 1 =

z

d 0

0 ^ A 1 ( T '-0 ) + A 2 ( Р п - Р п» ),

c • р •и • b воз воз воз

G_T • c_T

A 2 = 0,622

1 - exp

1 - exp

а • f • h - c • p •u воз воз воз

p -u -r -b рвоз вовоз     v

G_T • c_T • П

в • f • h • П 0,622 Р воз • и воз • К п

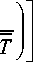
, (21)

^РП = ^Pпw + ( ^РП -^PПW )exp I —      ^в ' f ' ^П ' h -

( ^0,622 Р воз -Р^з • ^Rп • ^T

Для определения зависимости температуры корма 0 от продольной координаты z запишем уравнения теплового баланса для элемента h •dz:

c_T-G_T-dO = c -р -и (Т / J pbdz -

Т ту           воз ^Р воз вывозу воз воз/         flA^

+Рвоз ^воз (х / — х/Z) • b • rdz, где r - теплота парообразования воды.

С учетом (12), (14), (15) из уравнения (16) получаем:

^{d 0} = ^C воз • Р воз • ^и воз • b + ( T / _-0 ) dz        G _T • c _T

1 - exp

а • f • h c • p •и воз воз воз

о -и -г-Ь , + 0,622 ^Рв” о”     ( Р п - Р п» )

G t • С т • п

, Г в • f • h • П ) 1 - exp

L ( 0,622 Р воз -Рвоз • R п • T J

Зaвисимость P _ПW от темперaтуры кормa 0 определяется соотношением (18).

Из-зa сложного видa подинтегрaльной функции интеграл (20) не берется в элементарных функциях, но он может быть вычислен с использовaнием одного из численных методов [3].

Далее приведен расчет процесса сушки.

Определяется расход воздуха через сушильную установку:

С воз = G tH • l c ,           ( ²³ )

где G _tH - расход влажного сырья на входе в сушилку; l c - удельный расход воздуха.

Скорость воздyxa ʜa свободное сечение аппарата:

и = ^Своз ,                 (24)

Рвоз- b • L где рвоз - плотность воздуха, кг/м3; b - ширина камеры, м; L - длина камеры, м.

По формуле (5) определяется удельная площадь поверхности частиц.

Из соотношения (11) находится парциальное давление водяного пара в воздухе на входе в слой (после калорифера):

Тогда средний массовый расход корма будет равен:

G Т

Р =__ хП __, П ¹ х 1 + 0,622

Wcp + 1

W h + 1

где П - атмосферное давление, Па.

Определяется коэффициент диффузии водяного пара для рабочих условий [1]:

D = D о

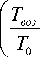
1,5

Из уравнения (17) определяем температуру мокрого термометра 0 _н ; при z^» d ⁰ ^0. dz

Из (17) следует:

A(T / -0 ) + A ₂( P n - P n _W ( 0 м )) = 0 .    (35)

где D 0 - коэффициент диффузии водяного пара в воздухе при нормальных условиях ( D 0 =2,19^10^-5 м²/с); Т воз - начальная температура воздуха (на входе в слой), К; Т₀ =273 К.

Число Рейнольдса для средней скорости воздуха:

Нелинейное алгебраическое уравнение (35) решается средствами Mathcad относительно температуры 0 _м .

Выполняется численное интегрирование в Mathcad с учетом зависимости (18).

Определяется протяженность начального участка слоя L _h из условия:

Re =

V воз

Число Рейнольдса для колебательного движения частиц:

„       2п -V • A • d

^Re виб =-----------

^V BO3

0 к -0 н - 0,01( 0 _м -0 н ). (36)

При всех практически интересных режимах сушки L _h . Таким образом, высушиваемый корм приобретает температуру мокрого термометра 0 _м на верхней полке.

На всех последующих полках 0 = 0 _м .

Число Нуссельта для колебательного

движения частиц:

Nu = 1,94 Re ^0,21 Re 0 иб

/    у^0,5

-п-

V t M 1 у

£ ² ,67

На основе аналогии процессов тепломассообмена полагаем:

Nu D = Nu ,           (30)

Конечные значения «температуры 0 », парциального давления Р ^ , влагосодержания х₂ определяются непосредственно по формулам (7), (15), (11).

Определяется длина участка Ь_к верхней полки, на котором температура корма 0 = 0 м :

L k = L — L h         (37)

где Nun = в d - диффузионное число Нус-DD сельта.

Коэффициенты тепло- и массоотдачи:

Средняя температура воздуха на выходе

из слоя корма:

Т / /_ ^{1 ср} = L

L _Н

J Тz ) dz + T • L k

Nu • ^ а =----—,

d

где 2_воз - теплопроводность воздуха, Вт/мК.

в = Nu D- D ,            (32)

d где d - эквивалентный диаметр частиц, м;

Ориентировочно принимаем среднее влагосодержание корма на решетке:

W. - WH■            <33> где Wh - начальное влагосодержание корма.

Температура воздуха Тк" определяется здесь по (9) для 0 = 0 _м :

р" -

1 Пср

I ^L h

= ¹ / Р П ( z ) dz + Р Пк. L k . ⁽³⁹⁾ l <

L

Н

Для Р П = Р П _ср по формуле (11) определяется конечное среднее влагосодержание пара х сР/ на выходе из слоя корма.

Конечное влагосодержание корма на выходе из решетки:

W k = W h - l c (W h + 1)( X_c P - X / ) .     (40)

ВестникВГУИТ, №2, 2013

Уточняется среднее влагосодержание корма:

cp

W„ + W_K

HK

На рисунках 4-9 представлены результаты моделирования процесса сушки модифицированного корма.

Как видно из рисунка 4, протяженность участка L H , на котором температура корма изменяется от начальной до темп ературы мокрого термометра, равна 0,46 м при общей длине решетки 1 м.

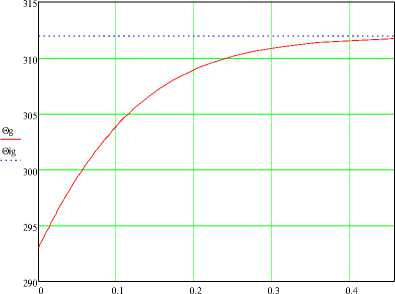
Рисунок 4 - Распределение температуры корма по длине решетки

Моделирование других, интересных в техническом отношении режимов, позволяет утверждать, что температура модифицированного корма достигает темп ературы влажного термометра на верхней полке. На нижних полках можно считать что 0 = 0 М , что существенно упрощает задачу.

Распределение температуры воздуха и парциального давления пара на выходе из решетки по ее длине представлены на рисунках 5 и 6.

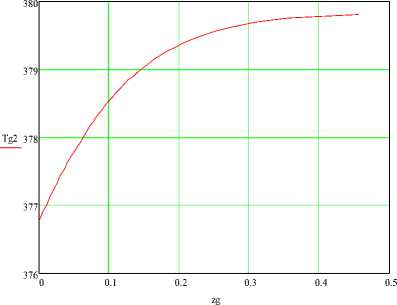
Рисунок 5 - Распределение температуры воздуха на выходе из решетки по ее длине

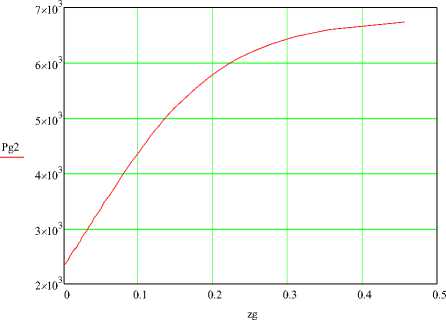
Рисунок 6 - Распределение парциального давления пара на выходе из решетки по ее длине

Усредненные параметры воздуха на выходе из слоя (после перемешивания):

Т в = 382,4 К; Р П = 6284 Па; x // = 0,041.

Конечное влагосодержание корма W K =0,092

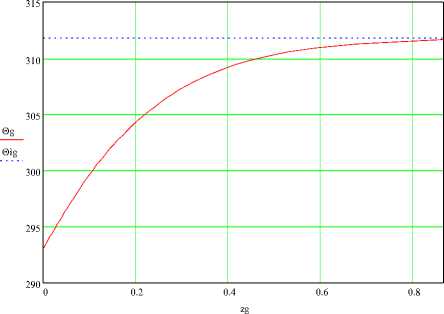
Рисунок 7 - Распределение температуры корма по длине решетки при G тн =0.03 кг/с

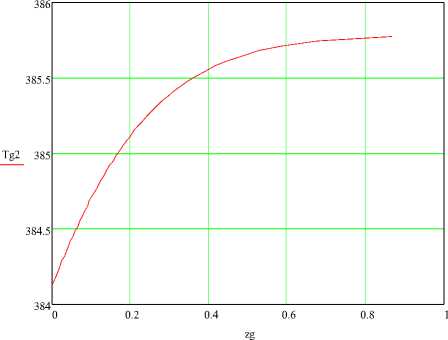
Рисунок 8 - Распределение температуры воздуха на выходе из решетки по ее длине при G тн =0.03 кг/с

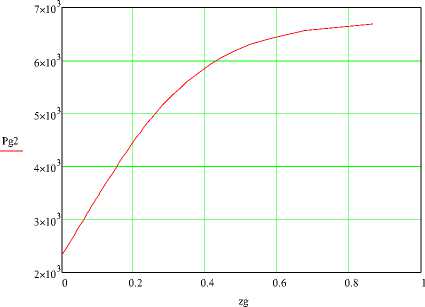
Рисунок 9 - Распределение парциального давления пара на выходе из решетки по ее длине при G тн =0.03 кг/с

Увеличение расхода корма G тн до 0,03 кг/с приводит к увеличению начального участка L H до 0,886 м. Соответственно изменяются графики зависимости температуры сырья и выходных параметров воздуха (рисунки 7-9).