Математическое моделирование процессов диффузии-адвекции радона в кусочно-постоянных анизотропных слоистых средах с включениями

Радон, в силу своих специфических особенностей, является индикатором при различных геологических и геотехнических исследованиях. Динамические изменения концентрации радона, в приповерхностном слое почвы отражают динамические изменения напряженно-деформированного состояния горного массива, что служит основой для исследования вариаций поля радона, как краткосрочного предвестника, сейсмических событий [1]. В геологии изотопы радона, используются для поиска, урановых и ториевых руд, для экологического картирования при выборе площадок под строительство промышленных и жилых сооружений. Повышенная концентрация радона, над залежами углеводородов используется для поиска, и оконтуривания нефтяных и газовых месторождений.

Изучение процессов распределения радона, в грунте и его стока, в приземный слой атмосферы связано с решением параболических краевых задач математической физики. Разработка. алгоритмов решения подобного типа, задач и расчета, полей объемной активности радона, имеет практическое значение в таких направлениях, как сейсмология, геохимия, разведочная геофизика, и т.д.

Постановка задачи и способ решения

Будем рассматривать горизонтально-слоистую модель среды с локальными включениями, отражающую типовую структуру нефтеносного района (см. рисунок).

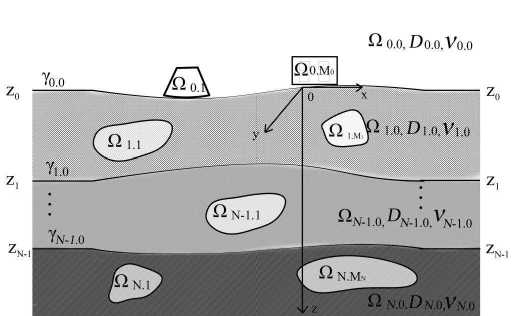
Горизонтально-слоистая среда с включениями

Пусть среда разделена гладкими параметрически заданными границами Y i. o = { Y i. o (x, y) l Y i. 0 ^ z i при V x 2 + У 2 ^ ^} (i = 0, N) на горизонтальные слои Q q . g , fi i . o ,..., Q n. o , заполненные веществом, диффузионные свойства которого описываются симметричными тензорами

D i o =

_d i_x._x 0 i. 0 xy i. 0

xz

i. 0 xy i. 0 yy i. 0 yz

i.0 xz i.0 yz diz.z0

и скоростями адвекции ν 0 _. 0 , ν 1 _. 0 , . . . , ν N_. 0 соответственно.

Каждый слой Q i. o содержит M i локальных включений ^ i.j (j = 1,M i ) с границами Y i.j , заполненных веществом, физические свойства которого описываются постоянными симметричными тензорами диффузии

D i.j ⁼

i.j xx i.j xy i.j xz

i.j xy i.j dyy i.j yz

i.j xz i.j yz i.j zz

и скоростями адвекции v ij ,i = 0,N,j = 1, M i .

Математическая модель переноса радона в области исследования Q = U N =0 j i o ^ i.j С R ³ может быть представлена начально-краевой задачей вида:

^дА ^ ^Р^ = div(D i.j V A i.j (P,t)) + V i.j ^dA i d P, t — A(A i.j (P,t) - A^),

P = P (x,y,z) G ^ i.j ,i = 0N,j   ", M;

A i.j (MVym = A i. o (P,t )\Y _i._j ,i = 0Л, j = 1ГЖ;

lim A N. o (P,t) = An.^, lim A o . o (P,t) = 0;

z→∞              z→-∞ lim       Ai.o(P,t) = Ai (P,t),i = p;

P ∈ Ω i.0 , x ² + y ² →∞

A i.j (P, 0) = 0, i = p, j = 0, M i .

Здесь A i.j (P, t) - объемная активность радона в грунте; А - постоянная распада радона; A i. ∞ – объемная активность радона, находящегося в радиоактивном равновесии с радием ( 226 Ra) в грунте i -го слоя, которая равна A i. ^ = K i.em A i.Ra P i.s (1 — n i )) , K i.em — коэффициент эманирования радона, A i_.R_a – удельная активность ²²⁶ Ra , ρ i.s – плотность твердых частиц, η i - пористость грунта, A i (P, t) - нормальное поле радона, описывающее диффузию-адвекцию радона в слоистой среде в предположении отсутствия включений. Переменная t >  0 - время.

Представим искомую функцию объемной активности радона в грунте A i_.j (P, t) в виде суммы двух вспомогательных функций нормального A i (P, t) и аномального A i.j (P, t) полей, т.е.

A i.j (P,t) = A i (P,t)+ A i.j (P,t),i = 0N,j   ", M,                     (2)

где нормальное поле радона определяется краевой задачей:

A i (P,t) | ₇ i.o = A i +i . o (P,t) | ₇ i.o ,i = 0,N — 1;

lim AN(P, t) = A^,; lim Ao(P, t) = 0; z→∞            z→-∞ lim       Ai(P, t) = Ai(z, t), i = 0, N; Ai(P, 0) = 0, i = 0, N,

P ∈Ωi,√x2+y2→∞ где Ai(z,t) - объемная активность радона в кусочно-однородной горизонтально-слоистой среде с плоско-параллельными границами z = zi, i = 0, N — 1 и коэффициентами диффузии di = dZZ'A = 0, N. Способ определения Ai(z, t) описан в [2].

С учетом задачи (3) аномальное поле радона удовлетворяет следующей краевой задаче:

^+v i +1 . 0 A i +1 . 0 ^(P; t^ YL o , i = 0, N — 1;

A i. o (P,t) | _{7 i}._o = A i +i . o (P,t) | _{7 i}.o ,i = 0,N — 1;                               (4)

(P,t) = ((D i. o — D i.j ) V A i (P,t),n) + (V i. o — V i.j )A i (P, t);      ( * )

A i.j (PA)k j = A i. o (P,t) | _{7 i}.j ,i = 07N, j = IP/ , ;

lim A i. o (P, t) = 0, i = 0, N; A i.j (P, 0) = 0, i = p, j = 0, M i .

P →∞

Cделаем в задаче (4) замену вида:

A i.j (P,t) = e

^Xt u i.j (P ‘ ,t),

где P ‘ = (x, y, z ‘ ), z ‘ = z + V i,j t.

Получим задачу:

u i.j (P ‘ ,t)) | ₇ i. 0 = u i. o (P ‘ ,t)) | ₇ ‘. 0 ,i = 07N,j = 17 M i ;

p lim u i. o (P ‘ ,t)=0, i = 0, N;

U i.j (P ‘ , 0) = 0,i = 07N,j = 0?м.

Применим к задаче (6) способ решения, описанный в работе [3], используя интегральное преобразование Лапласа

oo

F ^{(P ,} '^s)= iu-P-^t

с формулой обращения

u(P ‘ ,t)

c + i ∞

= 2ni / F^(P'^s)e s ^{, ds}- c - i ∞

Получим следующую краевую задачу:

div(D i.j Wi.j (P ‘ ,s)) - sF i.j (P ‘ ,s) = 0,P ‘ G ^_L j ,i = 0,N,j = 0,M i ;

F    (P ‘ ) = ((D i. o — D i.j ) V F (P ‘ , s), n) + (V i. o — V i.j )F (P ‘ , s);

Fi.j (P‘, s)lY‘.j = Fi.o(P‘,s)lY‘.j ,i = O, j = 1"Ж lim Fi.j(P‘,s) = 0,i = 0,N,

P′→∞ где функции F^i0(P‘) и Fi(P‘, s) - есть образы функций ^i.o(P‘, t) и Ai(P‘, t) при преобразовании (7) соответственно.

Для решения задачи (9) рассмотрим вспомогательную задачу для функции Грина G(P, Q) - функции точечного источника, находящегося в произвольной точке Q(x q , y q , z q ) и генерирующего диффузионное поле единичной интенсивности во вмещающем пространстве (в слоистой среде без включений):

G i. o (P ‘ ,Q) | Y ’. 0 = G i +1 . o (P ‘ ,Q) l Y ’. 0 ,i = 0,N — 1;

lim G i.j (P ‘ ,Q)=0,i = 0,N.

P ^′ →∞

Согласно [3], интегральное представление задачи (9) будет иметь вид:

N M i

F(P‘, s) = ^ ^   Fi.j(Q,s)[(vi.o — Vi.j)Gi.o(P‘,Q) + i=o j=1 /

^γ i^′.j

N M i

i =o j =1 ^γ i^′.j

Здесь n Q – вектор внешней нормали к границе включения в точке Q , а граничные значения функции F i.j (Q, s) находятся как решение системы интегральных уравнений Фредгольма второго рода, формируемых из (9) при P ^′ ∈ γ i.j :

N M i

F i.j (P ‘ ,s) —22 Е / F i.j (Q,s)[(V i. o

— V i.j )G i. o (P ‘ , Q)+

i =o j =1

^γ i^′.j

N M i

ЕЕ/ i=oj=1Vj

Таким образом, алгоритм решения исходной задачи (1) имеет вид:

Шаг 1. Определяем нормальное поле радона A i (z,t) в горизонтально-слоистой кусочнооднородной среде с плоско-параллельными границами z = z i = const, i = 0, N — 1 , коэффициентами диффузии d i = d ZZ ,i = 0, N и скоростями адвекции v i. o ,i = 0, N по алгоритму, описанному в работе [2].

Шаг 2. Если границы слоев z = Y i. o (x,y) = Z i = const, то есть среда имеет плоскопараллельные границы, то решение задачи (3) для нормального поля радона найдено: A i (P, t) = A i (z, t) . Иначе следует решить задачу (2), например, методом интегральных уравнений, формируя их по участкам Y i. o (x,y) = Z i .

Шаг 3. Вычисляем функции ^ i. o (P ‘ , t) на границах включений Y i.j ,i = 0, N, j = 1, M i по формуле (*).

Шаг 4. Для каждого из значений параметра s множества квадратурных узлов численного обращения преобразования Лапласа (в соответствии с алгоритмом в [4]) по формуле (8):

Шаг 4.1. Находим образы F ^ i 0 (P ‘ ) функций ^ i. o (P, t) при преобразованиях (5) и (7).

Шаг 4.2. Находим решение задачи (10) для функции Грина. Оно может быть получено аналитически для случая однородных слоев с плоско-параллельными границами с помощью интегрального преобразования Ханкеля-Вебера.

Шаг 4.3. Формируем систему (12) и находим ее решение – граничные значения функции F i.j (Q, s) .

Шаг 4.4. По формуле (11) определяем решение задачи (9) - функцию F i.j (P ‘ ,s).

Шаг 4.5. Формируем слагаемое квадратурной формулы для интеграла (8), вычисляя функции u(P ‘ , t) .

Шаг 5. Находим аномальное поле A i.j (P,t) по формуле (5).

Шаг 6. Решение исходной задачи (1) - функцию A i.j (P, t) - получаем по формуле (2).

Заключение

Построена математическая модель диффузии-адвекции радона в слоистых анизотропных средах с анизотропными включениями, которая представляет собой краевую задачу математической физики параболического типа. Предложен комбинированный способ решения задачи на основе методов интегральных преобразований, интегральных представлений и граничных интегральных уравнений. Построен алгоритм расчета поля объемной активности радона.