Математическое моделирование процессов эвтрофикации в мелководных водоемах на многопроцессорной вычислительной системе

Изменение природно-климатических условий и антропогенное воздействие приводят к эвтрофикации вод мелководных водоемов, приводящей к значительному росту популяций фитопланктона, многие виды которого являются токсичными, вызывают тяжелые заболевания у людей. Процессы эвтрофикации влияют на качество вод, состояние рыб-

Статья рекомендована к публикации программным комитетом Международной научной конференции «Параллельные вычислительные технологии – 2016».

ных запасов водоемов, в связи с этим разработка программно-алгоритмического инструментария имеет не только научное, но и важное народнохозяйственное значение, она позволит осуществлять предсказательное моделирование взаимосвязанных процессов эвтрофикации на основе натурных экспериментов, полученных в ходе экспедиционных работ в акватории мелководных водоемов.

Целью работы являлось построение и численная реализация математической модели эвтрофикации вод мелководного водоема, обладающей предсказательной ценностью. В соответствии с поставленной целью решены следующие задачи: изучена предложенная модель эвтрофикации вод мелководного водоема, получены достаточные условия существования и единственности ее решения; разработан и исследован дискретный аналог этой модели. В работе описана построенная библиотека двухслойных методов вариационного типа, предназначенных для решения сеточных уравнений с самосопряженными и несамосопряженными операторами, возникающими при дискретизации разработанной модели, на многопроцессорной вычислительной системе. Для равномерного распределения вычислительной работы между процессорами использовался k-means алгоритм.

Предложенные модели и методы были применены при разработке программного комплекса, предназначенного для расчета значений концентраций планктона и загрязняющих примесей в Азовском море. Входными данными предложенной выше модели эвтрофикации вод мелководного водоема вида (1) – (3) является поле вектора скорости водной среды, рассчитанное по моделям Сухинова А.И., Чистякова А.Е. [3–6]. Статья организована следующим образом. В разделе 1 приводится разработанная математическая модель эвтрофикации вод мелководного водоема, а также ее исследование на непрерывном и дискретном уровне. Раздел 2 содержит описание разработанных методов вариационного типа для решения, возникающих в процессе дискретизации, сеточных уравнений. Раздел 3 посвящен описанию параллельного алгоритма реализации метода минимальных поправок. Раздел 4 содержит описание программного комплекса, численно реализующего модельную задачу эвтрофикации мелководного водоема. Раздел 5 посвящен описанию и анализу результатов численных экспериментов. В заключении приводятся итоги исследования.

1.    Трехмерная математическая модель эвтрофикации мелководного водоема

Азовское море является внутренним морем расположено на востоке Европы. Его глубина не превышает 13,5 метров и является самым мелким морем в мире. Азовское море подвержено эвтрофикационным процессам в виду своей мелководности. Эвтрофикация (др. греч. εὐτροφία — хорошее питание) — это процесс обогащения морей, озер и рек биогенными веществами, сопровождающийся повышением объемов растительности в водоемах. Эвтрофикация может возникать как результат антропогенного воздействия, так и естественного старения водоема. К химическим биогенным элементам, способствующим эвтрофикации водоема, относятся азот и фосфор. Морские течения, зависящие от рельефа водоема, оказывают влияние на биогенный режим.

При построении модели эвтрофикации вод (ЭВ) Азовского моря и Таганрогского залива использовались работы Матишова Г.Г., Ильичева В.Г., Якушева Е.В., Сухино-ва А.И. [1], Крукиера Л.А., посвященные математическому моделированию гидрохимических процессов. В данных моделях учтено, что при штилях и малых ветрах в придон- ных слоях Азовского моря возникают анаэробные условия. Отсутствие течений в приповерхностных донных слоях влечет за собой высвобождение в раствор (кроме сероводорода) аммония, сульфатов, органических соединений, силикатов и фосфатов, двухвалентного марганца и железа. Расчетная область G представлена на рис. 1.

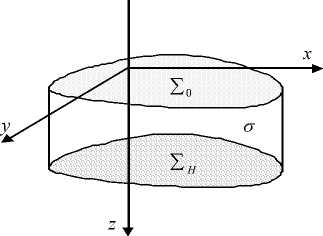
Рис. 1. Схема расчетной области G

G представляет собой замкнутую область, ограниченную невозмущенной поверхностью водоема S 0 , дном S _H = S _H ( x , у ) и цилиндрической поверхностью о для 0 <  t <  T 0 . У = У 0 U У _H ио — кусочно-гладкая граница области G .

Модель будет иметь вид:

,        д S i        д S i     z          х д S i                   д ( д S i А

S, + и --- + v --- + (w — w )--- = ^ A S. + v + V<, i,t                                                           gi                      i i                   i                      i д x ду               д z              д z V д z )                   (1)

где Si — концентрация i -й примеси, i = 1, 17 , индекс i указывает на вид субстанции, i = 1, 17 : 1 — сероводород (H2S); 2 — элементная сера (S); 3 — сульфаты (SO4); 4 — тиосульфаты (и сульфиты); 5 — общий органический азот (N); 6 — аммоний (NH4) (аммонийный азот); 7 — нитриты (NO2); 8 — нитраты (NO3); 9 — растворенный марганец (DOMn); 10 — взвешенный марганец (POMn); 11 — растворенный кислород (O2); 12 — силикаты (SiO3 — метасиликат; SiO4 — ортосиликат); 13 — фосфаты (PO4); 14 — железо (Fe2+) 15 — кремнекислота (H2SiO3 — метакремневая; H2SiO4 — ортокремне- вая); 16 — фитопланктон; 17 — зоопланктон; и = (и, v, w) — скорость водного потока; wgi — скорость осаждения i-й компоненты; цi, vi — коэффициенты турбулентного пе- ремешивания по горизонтальному и вертикальному направлениям соответственно; Vi — функция, описывающая химико-биологический источники (сток), а также агрегирование (слипание-разлипание), если соответствующая компонента является взвесью.

Система (1) рассматривается при следующих граничных условиях:

д S.                                                   ,                                                       ,

S i = 0 на о , если U n <  0; —- = 0 на о , если U n >  0; S i z = 0 на S ₀ ; S i z = -e i S i на S _H , ( 2 ) д n                                                ^,                         '

где e i — коэффициент поглощения i -й компоненты донным материалом.

Необходимо также добавить начальные условия:

S i

1 1 =0

= S i ₀ ( x , у , z ), i = 1, 17.

Проведено исследование трехмерной модели ЭВ Азовского моря вида (1) – (3), получены достаточные условия существования и единственности ее решения, сформулиро- ванные в виде теорем.

Теорема 1. Пусть S i ( x , у , z , t ) ,     v i e C ²( U_t ) ⁿ C ( U_t) , где U_t = G ^x (0 <  t <  t ₀);

^i = const > 0; U = (u, v, w — wgi), vi(z) e C\G); Sio e C(G), i = 1,17 . Тогда при вы- полнении неравенств: max {Mi, vi} - -1 max {|pi |} > 0

G                          ⁰ G

V i = P i ( S j ) S i + V i , i * j ; V i = ^LSi - DS i - P i S i , LS i

для всех i = 1, 17 ,

где

d S i d t

+ div ( S i U i ) ,

DSi = Mi A Si + — Ui ^Si- 1,  1 = П (1 / LX + 1 / Ly + 1 / LX);  Lx, Ly, Lz — простран- d z V d z 7

ственные максимальные размеры расчетной области; модельная задача эвтрофикации мелководного водоема ЭВ вида (1) – (3) имеет решение.

Теорема 2. Пусть Si(x, y, z, t), vi e C 2mt) n CMt), Mi = const > 0; и, vi(z) e C 1(G), i = 1, 17 . Тогда при выполнении неравенств: 2Mi (1 / ь2x + 1 / Ly) + 2vi / L > ф1 для всех i = 1,17 (где функции ф1 определяются источниками загрязняющего вещества (ЗВ)) модельная задача ЭВ мелководного водоема вида (1) – (3) имеет единственное решение. Для дискретизации модели (1) – (3) построим в области решения задачи связ- ную сетку rnh . hx, hy, hz — векторные параметры, характеризующие плотность расположения узлов:

® _h = { X j = jh_x , У к = kh y , Z i = lh z ; j = 0, N , ; к = 0, N y ; 1 = 0, N z ;

Nxhx = LX, Nyhy = Ly, Nzhz = Lz} , ®hT = ®h X ®r, ®r = {tn = nT, n = 0, Nt } , где i, j, к — индексы по направлениям x, y, z; Nx, Ny, Nz — количество узлов по коор- динатным направлениям.

Расчетная область по пространственным

направлениям x , y , z представляет собой

объединение параллелепипедов. Дискретизируем модель (1)

– (3) с помощью разностной

схемы с весами:

q П + 1

S

^^^^^^.

S n

+

n u

Y ^Sn + U,к ,i

+ (1

^^^^^^.

Y ^{) S} n ) j +1, к , 1

^^^^^^в

(

+

+

^^^^^^в

^^^^^^в

^^^^^^в

^^^^^^в

+

n v

V

Г/

( w n

V

( wn.

т

V

2h x

n u

Y S n + U-к ,1

+ (1

^^^^^^в

Y ^{) S} n ) j -1, к , 1

л

1,

2h x

+

Y S n +1, к +1, 1

+ (1

^^^^^^в

2hy

^^^^^^в

^^^^^^в

M i      n ⁺¹

_h 2 ^{( Y} S ( i ) j + 1 x

M i

h2y

hz

hz

n

w g (i)j,к,1 +

n w , x g (i) j,k ,1

- , к , 1

^{( YS} ( i ) j , k + 1, 1

(

n

+ (1

+ (1

^^^^^^в

^^^^^^в

U

V

( i ) j, к,1 +

v

V

< j

n

1,

'2

( i ) j , к ,1 -12

< N x

^^^^^^.

Y ^)Sni ) j , к +1, 1

Y S?- +¹

⁽ i ) j,

Y S n +¹

^{7 (} i ) j,

^{/ ) S} ( i ) j + 1, к , 1

^{/ ) S} ( i ) j , k + 1, 1

^YS ( i ) j , k , 1 + 1

/ S n +¹_t , •    ( i ) j ^{, k , 1}

^^^^^^в

n v

/ S?- +¹

'    ⁽ i ) j ,

+ (1

^^^^^^в

2hy

+ (1

^^^^^^в

2h z

+ (1

^^^^^^в

2 h

z

^^^^^^в

^^^^^^в

+ (1

+ (1

^^^^^^в

^^^^^^B

1,1 <  к <  N y

Y ^)Sni )

Y ^{) S} n )

2 Y S n +¹

' ( i ) j ,

! ,к ,1

^^^^^^в

2(1

^^^^^^в

^^^^^^в

^^^^^^в

Y ^{) S} ( i:

:) j , к ,1

)

^^^^^^в

2 / S ,ⁿ +¹„ , ' ( i ) j ^{, k , 1}

Y)S?x ■„ , • ( i ) j ^{, к,1}

Y ) S ?

• •     ( i ) j ^{, к,1}

^^^^^^.

+1

^^^^^^в

hz

^^^^^^B

^^^^^^в

2(1

^^^^^^в

^Y)S ( i ) j , k , 1

)

^^^^^^в

Y S n +^{1 (} i ) j ,

/ S n +¹₁ , • ( i ) j ^{, k , 1}

hz

1,1 <  1 <  N_z

!, к ,1

^^^^^^в

^^^^^^в

Y )S ( i

^^^^^^B

^^^^^^B

^^^^^^.

Y ^)S ?! )

+

M i      n ⁺¹

h 2 ^{( Y} S ( i )

x

j - 1,к ,1

+ (1

^^^^^^в

Y )S ?

< ' ( i ) j -1, к , 1

)

^^^^^^в

M i      n ⁺¹

h 2 ( ' ° ( i ) j , k -1, 1

+ (1

^^^^^^в

Y)SL ■ r _x i ( i ) j , k -1, 1

y

)

^^^^^^в

) ^{j,k 1}

+

Y )S n

• •     ( i ) j ^{, k , 1}

1, i = 1, 17.

-.

^^^^^^B

V i

0,

К

системе (4) добавим аппроксимированные начальные и граничные условия. Ис- следуем устойчивость разностной схемы (4) для этого запишем ее в каноническом виде:

D О ^{n + 1}

^B 1 ^S ( i ) j +1, k , l

n + 1                  n + 1                  n + 1

^{+ B} 2 S ( i ) j , к + 1, l  ^{+ B} 3 S ( i ) j , к , l + 1 ⁺ A 1 S ( i ) j , k , l

^^^^^^.

D О ^{n + 1}

^B4 S ( i ) j -1, k ,l

^^^^^^.

^^^^^^.

D Q n ^{+ 1}

^B 5 S ( i ) j,k -1, l

^^^^^^.

^{+ B} 9 S ( i ) j,k ,l + 1

^^^^^^»

D Q n ^{+ 1}

^B 6 S ( i ) j,k,l -1

n

^B10^B ( i ) j - 1,к,l

^^^^^^.

1 <  j <  N_x

^^^^^^.

- A S ⁿ     + B S ⁿ + B S ⁿ +

2 ( i ) j , k , l          7 ( i ) j + 1, к , l          8 ( i ) j , к + 1, l

^B11 S ( i ) j,k -1, l

^^^^^^.

n

^B12^B ( i ) j, k,l -1

^^^^^^.

V ,

1,1 <  к <  N - 1,1 <  l <  N - 1,0 <  n <  N - y                           z                           t

1, i = 1,

Достаточное условие монотонности и устойчивости модели (4) определяется нове принципа максимума А. А. Самарского при следующих ограничениях:

на

ос-

h x < ||² A / u n

, h

I с ( ч ) ' ^у

< 22^ / v

, h < I с ( ™ h ) ' z

||^2vi / ( wn

^^^^^^.

w g I

, i = 1, 17. ¹C ( Ч )

Исследование погрешности аппроксимации разработанной схемы с весами вида (4) показало, что при у = 0.5 (схема Кранка — Николсон) она имеет наибольший порядок точности по временной и пространственным переменным: O ( г² + | h |²), где

¹у ⁺ h z •

2.    Метод решения сеточных уравнений

Дискретную модель (4) может быть представлена в виде операторного уравнения: Au = f                                               (7)

с положительно определенным оператором A в гильбертовом пространстве H . Рассмотрим неявный двухслойный процесс вида

B y k ^{+ 1}

T

^^^^^в

— + Ay_k = f, к = 0,1, ...

k

с неким начальным приближением у0 е H и оператором — предобуславливателем в [7]. Всякий двухслойный итерационный процесс (8), характеризуется операторами A и B , энергетическим пространством HD , в котором исследуется сходимость метода, и спо- собом расчета итерационных параметров гк • К основным вопросам теории итерацион- ных методов решения сеточных уравнений относится оптимальный выбор параметров гк [8–10].

Для вычисления параметров г _к в методах вариационного типа не требуется априорная информация об операторах задачи (7) (кроме условий общего вида A = A * >  0 , ( DB ^{- 1} A ) = DB ^{- 1} A ). Данные методы основаны на принципе: если задано значение у_к , а у_{к +1} находится по схеме (8), то параметр г _{к +1} рассчитывается из условия минимизации в

HD энергетической нормы погрешности zk+1 = ук+1 - и , где и — решение уравнения (7). Последовательность ук, рассчитанная на основе выражения (8), в которой значения гк вычисляются из приведенного выше условия, является минимизирующей для квадратичного функционала вида I (у) = (D (у - и), у - и) • Данный функционал имеет ограничения снизу (в силу положительной определенности оператора D ), и его значение достигает минимума, равного нулю при у = и • Выбор параметра гк+1 из приведенного условия гарантирует локальную минимизацию функционала I (у) при переходе от ук к ук+1 • В случае задания оператора-предобуславливателя методом простой итерации

( B = E ) переход от у_к к у_{к +1} осуществляется согласно выражению

У к +1 = У к

^^^^^^.

^гк + 1^гк , ^гк = ^A У k ^- f •

ента для функционала ( A ( y - u ) , y - и ) в точке y_k . В направлении антиградиента происходит наискорейшее убывание значения функционала. Параметр т _к +1 в H D находится из условия минимизации нормы погрешности z k +1 = y k +1 - и [11].

Формула для вычисления итерационного параметра т _{к +1} находится в предположении невырожденности оператора A . Погрешности находятся из уравнений: z_k = y_k - и , к = 0,1,™ . Схема (8) с учетом y k = т _к + и , примет вид: z k ₊ 1 = ( e - т _кв - 1 a ) z k , k = 0,1,™, z ₀ = y ₀ - и . С помощью замены z_k = D - ^1/2x_k осуществляется переход к выражению, содержащему только один оператор:

Х к +1 = S k +1 Х к , S k = E ^- T C, C = D - ^1/2 ( DB - 1 A ) D -^1/2 .                       ⁽⁹⁾

С помощью равенства || z_k|| D = || x_k || (|| ■ || D — норма в H D , || ■ || — норма в н ) описанную задачу расчета параметра T _{k +1} можно описать следующим образом: рассчитывается значение параметр T _{k +1} из условия минимизации нормы x_{k +}1 в пространстве н . Рассмотрим норму:

II ^xk +11Г = (( E ^{- T}k +1 C ) ^xk , ( E ^{- T}k +1 C ) ^xk ) = UNI^{2 -} т +1 ( ^Cxk , x ) + N ( ^Cxk , ^Cxk ) = (10) = ( ^Cxk , ^Cxk ) [ ^Tk +1^- ( ^Cxk , ^xk ) / ( C ^xk , ^Cxk ) ] ² + INI^{2 -} ( ^Cxk , ^xk ) ² / ( ^Cxk , ^Cxk ) .

Оператор C не вырожден, поскольку не вырожден оператор A . Таким образом, для любого x_k имеем ( Cx_k , Cx_k ) > 0 , и минимальное значение нормы x_{k +}1 достигается при

Т+1 = (Cxk, xk) / (Cxk, Cxk) .

Подставим (11) в (10) и получим:

II xk+1|| = Pk+1 INI, где pk+1 = 1 - (Cxk, xk )2 / {(Cxk, Cxk) (xk, xk)}.

Выражение (11) описывает оптимальные значения итерационного параметра T _{k +1} .

Выражение (11) с учетом x_k = D ²z_k запишется в виде:

Tk+1 = (DB-1 Azk, zkxk ) / (DB-1 Azk, B-1 Azk ) , k = 0,1, ... .

Принимая во внимание, что Az_k = Ay_k - Au = Ay_k - f = r_k — невязка, а B ^-1 r_k = ®_k — поправка, выражение для расчета параметра T _{k +1} запишется в виде:

• Tk+1 = (D®k, zk) / (D®k, ®k), k = 0,1, ™ ,

а двухслойная итерационная схема (8) представима в явном виде:

yk+1 = yk - Tk+1®k, k = 0,i,..., то алгоритм для данного метода, запишется в виде:

• 1)    для вектора y_k вычисляется вектор невязки r_k = Ay_k - f ;

• 2)    вычисляются значения вектора поправки из уравнения B ® _k = r_k ;

• 3)    рассчитывается параметр T _{k +1} из выражения (15);

• 4)    рассчитывается новое приближение y_{k +1} из выражения (16).

Рассмотрим двухслойные градиентные методы, которые использованы при решении модельной задачи эвтрофикации вод мелководного водоема. Каждый метод из данного класса имеет свою область применимости и определяется способом задания оператора D. Оператор D выбирается таким образом, чтобы выражение (15) для итерационного параметра тк+1 содержало только известные величины.

Если оператор A самосопряжен и положительно определен в H , то для решения (8) можно использовать метод скорейшего спуска (МСС). Если оператор A невырожден и несамосопряжен, а оператор BA является положительно определенным, то применим метод минимальных невязок (ММН) [12]. С учетом Az k = Ax k - f = r_k и A = A * и выражения (15) получим формулу для расчета итерационного параметра т _{к +1} согласно методу скорейшего спуска:

Т +1 = ( r k ^- ® k ) / ( ^A ® k ^{- A} ® k ) ^{- k} = 0, 1, - .                          ⁽¹⁷⁾

Для случая в = E получим ю_к = B ^{- 1} r_k = r_k и выражение для расчета T _{k +} 1 примет вид:

^т к +1 = ( ^r k ^{- r} k ) / ( ^Ar k ^{- Ar} k ) ^{- к} = 0 ^{- 1-} - •                              ⁽¹⁸⁾

При решении модельной задачи (1) – (3) методом скорейшего спуска по невязке параметр T _{k +1} рассчитывается по формуле (18), а метод скорейшего спуска по поправке реализуется с помощью расчетной формулы (17).

Метод минимальных поправок (ММП) можно применять для решения модельной задачи (1) – (3) в случае любого несамосопряженного невырожденного оператора A , кроме того требуется положительная определенность оператора B A . Для метода минимальных невязок D = A * A .

Формула для итерационного параметра T _{k +1} в ММП имеет вид:

Т _к + 1 = ( A ® k - r k ) / ( A ® k - A ® k ) - k = 0-1- — •                          (19)

В случае ( в = e ) требуется положительная определенность оператора A- а формула для T _{k +1} примет вид:

Т +1 = ( ^Ar k ^{- r} k ) / ( ^Ar k ^{- Ar} k ) ^{- k} = ^{0- 1-} — •                          ⁽²⁰⁾

В таблице приведены результаты сравнения скоростей сходимости двухслойных градиентных методов вариационного типа, используемых для решения задачи эвтрофикации вод мелководного водоема вида (1) – (3).

В таблице используются следующие обозначения: метод минимальных невязок (ММН); метод минимальных поправок (ММП); метод скорейшего спуска по невязке (МССН); метод скорейшего спуска по поправке (МССП); p — номер итерации; n — номер временного слоя; 1 _ф — количество итераций, необходимое для сходимости метода решения СЛАУ для уравнения, описывающего изменение концентрации ф , Ф е { S - X } - где S = S ₅ - X = S ₁₆ .

Метод минимальных поправок (ММП) был выбран в качестве основного метода в виду его наибольшей скорости сходимости, согласно данным, приведенным в таблице.

Таблица

Сравнение скоростей сходимости методов вариационного типа

ММП
n p	1	2	3	4
1	I s = 48, I x = 44	I s = 47, I x = 43	I s = 47, I x = 43	I, = 4 8, I„ = 42 SX
2	I, = 53, I„ = 48 SX	I, = 52, I„ = 47 SX	I, = 53, I„ = 4 6 SX	I = 53, I = 45 SX
3	I, = 21, I„ = 21 SX	I, = 22, I„ = 20 SX	I, = 22, Ix = 19 SX	Is = 21, Ix = 19 SX
4	Is = 17, Ix = 15 SX	Is = 14, Ix = 13 SX
ММН
1	I S = 83, Ix = 65	I S = 77, Ix = 64	I S = 7 6, Ix = 63	I S = 7 6, Ix = 62
2	I S = 87, Ix = 73	I S = 87, Ix = 73	I S = 8 6, Ix = 72	I S = 85, Ix = 71
3	I S = 51, Ix = 51	I S = 50, Ix = 4 6	I S = 4 9, Ix = 43	I S = 4 8, Ix = 4 0
4	I S = 40, Ix = 38	I S = 38, Ix = 35
МССП
1	I S = 6 9, I X = 62	I S = 67, Ix = 61	I S = 67, Ix = 60	I S = 67, Ix = 59
2	I, = 71, Ix = 68 SX	Is = 74, Ix = 67 SX	Is = 74, Ix = 67 SX	I, = 74, Ix = 66 SX
3	I = 35, I = 32 SX	I = 35, I = 30 SX	I = 35, I = 2 9 SX	I, = 34, Ix = 28 SX
4	I, = 24, Ix = 23 SX	Ix = 21, Ix = 20
МССН
1	I = 68, I = 64 SX	Is = 7 9, Ix = 67 SX	I = 78, I„ = 66 SX	I = 7 8, I„ = 65 SX
2	I = 8 6, I = 74 SX	I = 87, Ix = 73 SX	I = 8 6, I„ = 73 SX	I = 8 6, I„ = 72 SX
3	I S = 53, I S = 4 9	I S = 52, Ix = 45	I S = 51, Ix = 42	I S = 4 9, Ix = 41
4	I S = 40, Ix = 38	I S = 36, Ix = 35

3.    Параллельный вариант метода решения сеточных уравнений

Для геометрического разбиения расчетной области с целью равномерной загрузки вычислителей (процессоров) МВС использовался метод k-means, который позволяет найти центры подобластей: Q = Q(3 на основе на минимизации функционала суммарной выборочной дисперсии функции, описывающей расположение элементов (расчетных узлов сетки). Пусть Xi — множество элементов i - ой подобласти, i е {1,..., m} , m — количество подобластей. Q(3) = ^ г1г 22 d2x, c) ^ min , где c = ~Т 22 x — центр v ixi|xexi                                        Xi | xexi подобласти Xi , а d(x, ci) — расстояние между центром подобласти ci и элементом x в Евклидовой метрике. Метод k-means позволяет разбить исходную область на примерно равные подобласти.

Результат работы метода k-means для модельных двумерной и трехмерной областей представлен на рис. 2.

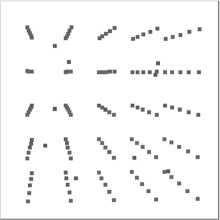
Рис. 2. Декомпозиция области на основе алгоритма k-means: для двумерной (на 9, 38, 150 подобластей); для трехмерной (на 6 и 10)

Опишем работу максиминного алгоритма. Начальное расположение центров подобластей задаются расчетными узлами сетки следующим образом:

• 1)    первый центр подобласти задается первым элементом;

• 2)    второй центр расположен на максимальном удалении от первого центра подобласти;

• 3)    каждый следующий центр подобласти располагается из условия на максимального удаления от ближайшего центра.

Опишем алгоритм работы k-means.

• 1)    Рассчитываются начальное расположение центров подобластей при помощи мак-симинного алгоритма.

• 2)    Все элементы кластеризуются на m клеток Вороного согласно методу ближайшего соседа, т. е. для любого x е X c , где X c — подобласть, должно выполняться условие ||x - s c || = min || x - s i ||, где s c - центр области X c .

• 3)    Расчет новых центров осуществляется согласно выражению s ^ ) = ।---1 ^ x .

X ^{k )}| x е^ >

• 4)    Выполняется проверка условия остановки алгоритма s^⁺¹ = s^) для всех к = 1, ..., m. Если условие остановки алгоритма не выполняется, то переходим к пункту 2.

4.    Описание программного комплекса

Элементы, лежащие на границах подобластей, обмениваются данными при параллельной реализации алгоритмов решения сеточных уравнений. Задача построения выпуклой оболочки решалась с помощью алгоритма Джарвиса. На основе данного алгоритма найдено расположение элементов, участвующих в обменах данными между вычислителями, и номера вычислителей, передающих и принимающих соответствующие данные [13, 14].

Метод сдваивания был использован для расчета итерационного параметра т при решении сеточных уравнений методом минимальных поправок. Следует отметить, что синхронизация разработанного алгоритма решения задачи (1) – (3) производится только при решении сеточных уравнений ММП на переходах между итерационными слоями.

Для решения модельной задачи эвтрофикации мелководного водоема (1) – (3) был создан комплекс прикладных программ, позволяющий производить расчеты концентраций загрязняющих веществ (ЗВ), фито- и зоопланктона в областях сложной формы (Азовское море и Таганрогский залив) [15].

С помощью созданного комплекса программ можно осуществлять:

• •    внедрение системы и совершенствование комплексного рыбохозяйственного мониторинга в водоемах (кормовых запасов и базы промысловых объектов наблюдение, прогноз и оценка состояния режима экосистем);

• •    разработку, согласование предложений и мероприятий по обеспечению оптимального режима, сохранения биоразнообразия промысловых ресурсов, экосистем мелководных водоемов;

• •    совершенствование методологии природоохранных исследований, разработка новых, апробация и внедрение перспективных методов изучения состояния водных экосистем и отдельных компонентов;

• •    разработку и совершенствование методов диагностики токсического воздействия ЗВ на гидробионты, в том числе ранней и дифференциальной диагностики токсикоза, а также поиск средств антидотной защиты водных экосистем;

• •    организацию и проведение исследований по выявлению тенденций и закономерностей изменения состояния водных экосистем под воздействием антропогенных факторов, разработка предложений и мероприятий по снижению и предупреждению таких воздействий;

• •    оценку ущербов рыбному хозяйству, наносимых разными видами хозяйственной деятельности, разработку предложений по предотвращению, уменьшению и адекватной компенсации ущербов.

Значения поля скоростей движения водной среды, рассчитанные в работах [16], относятся к входной информации для моделей гидробиологических процессов, описанных в первой главе. Для математического моделирования гидробиологических и гидродинамических процессов в трехмерной области сложной формы — Азовское море и Таганрогский залив использовались последовательно сгущающиеся прямоугольные сетки размерностями: 251 х 351 х 15 , 502 х 702 х 30 , 1004 х 1404 х 60 , ....

Начальное распределение загрязняющих веществ и планктона было учтено в форме, соответствующей пространственно-временным масштабам моделируемых процессов. Разработанный алгоритм численного решения поставленной задачи позволяет свободно варьировать значениями соответствующих параметров, видами управляющих функций и граничные условиями [17]. Понимание механизма функционирования системы и знание ее основных характеристик позволили для преодоления трудностей при настройке программы использовать феноменологический подход. Эффективность такого подхода связана с тем, что адекватность описания поведение экологической системы часто определяется точностью не отдельных параметров, а их соотношений.

Калибровка и верификация разработанной модели эвтрофикации вод мелководного водоема проводились на основе экологических данных по Азовскому морю, полученных в ходе научно-исследовательских экспедиций, проводимых учеными ЮФУ, начиная с 2000 года. В ходе исследований акватории Азовского моря изучались: виды и концентрации основных загрязняющих воды Азовского моря веществ; пространственные рас- пределения солености и температуры; кислородный режим; видовой состав фито- и зоопланктона; механизмы возникновения и развития заморов в центрально-восточной части водоема. Обработка экспедиционных данных заключалась в оцифровке, пересчете в стандартные единицы, классификации для использования в разных модельных задачах гидробиологии моря.

На рис. 3 приведена схема разработанного программного комплекса.

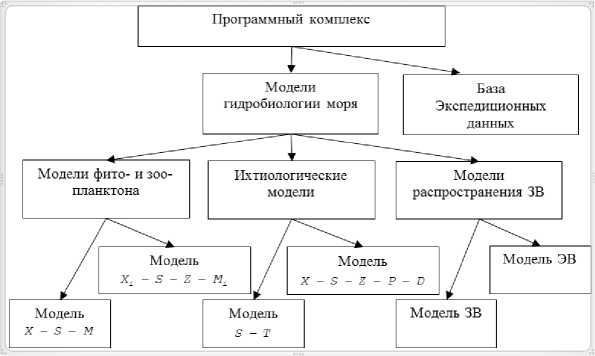
Рис. 3. Схема программного комплекса

Программный комплекс включает: блок управления, базы океанологических и метеорологических данных, системы интерфейсов, системы ввода — вывода и визуализации. Комплекс программ обладает удобным интерфейсом и обеспечивает ввод данных в диалоговом режиме. Построенный программный комплекс имеет универсальный характер и привязка его к условиям моделируемых районов и объектов осуществляется, как правило, на уровне входной информации. Для практического использования модулей требуется создание специальной информационной базы, содержащей сведения о параметрах, определяющих источники примесей, о климатических и физико-географических условиях исследуемых объектов.

При разработке программного комплекса использовался язык высокого уровня С++. Были разработаны две версии параллельного алгоритма решения модельной задачи эвтрофикации вод мелководного водоема. Первая предназначена для ЭВМ с операционной системой Windows, основана на технологии создания в этой системе дополнительных потоков. Вторая может использоваться для кластерных систем, и основана на технологии передачи сообщений (MPI).

5.    Результаты численных экспериментов

При моделировании пространственно-неоднородных процессов эвтрофикации вод Азовского моря (1) – (3) учитывалась внешняя периодичность, приводящая к усложнению системы. При этом колебания плотности планктона могут быть столь велики, что не могут быть объяснены случайными флуктуациями, и визуальная картина такова, что сравнительно небольшие площади высокой плотности («облака», «пятна») разделены пространствами с различными плотностями, зачастую не фиксируемыми общепринятыми методами наблюдений. Особенно ярко это явление выражено в тех местах водоема, для которых характерна потребность в биогенных элементах. При моделировании процессов эвтрофикации учитывался вегетационный период фитопланктона.

Диффузные процессы сглаживают пространственное распределение и рассеивают «пятна». Одна из попыток объяснить парадокс стабильности «пятен» с помощью численных экспериментов заключалась в предположении об активном передвижении гетеротрофных организмов (зоопланктона и рыб) в направлении градиента «пищи», что обеспечивает закрепление пространственной неоднородности биогенных веществ в водной среде. Устойчивая пространственная неоднородность распределения может быть, например, связана с диффузионными процессами и наличием у фитопланктона механизма эктокринного регулирования, т.е. регулирования скорости роста водорослей посредством выделения в среду биологически активных метаболитов.

На рисунке 4. показаны результаты расчета концентрации загрязняющего биогенного вещества для модели (1) – (3) (начальное распределение полей течений при северном ветре). Приведенные ниже рисунки отражают влияние структур течений водного потока в Азовском море на распределение загрязняющего биогенного вещества и фитопланктона. Белым цветом выделены максимальные значения концентраций биогенного вещества (азота) и фитопланктона черным — минимальные.

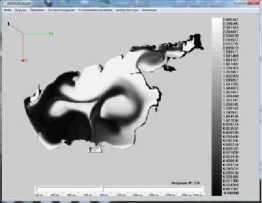
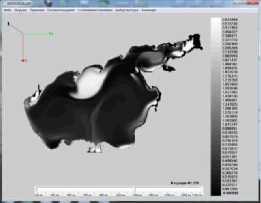
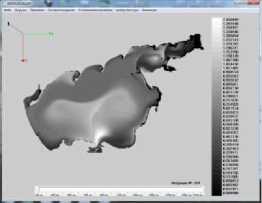
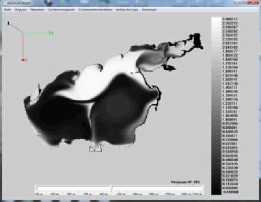
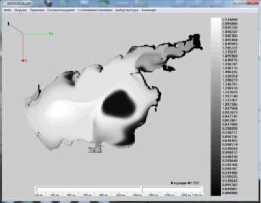
Рис. 4. Распределение концентрации загрязняющих веществ в различные моменты времени

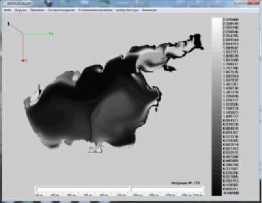
Результаты моделирования динамики фитопланктона в Азовском море представлены на рис. 5. ( N — номер итерации, начальное распределение полей течений водного потока при северном направлении ветра).

Критерием проверки адекватности построенных моделей гидробиологии мелковод- ного водоема служила оценка погрешности моделирования с одновременным учетом натурных данных по имеющимся n замерам, которая вычислялась по формуле: 5 = ЛДSknat - Sk U Л Sk nat , где Sknat — значение концентрации загрязняющей к=1                               к=1

примеси, полученное с помощью натурных экспедиционных измерений; S_k — значение, рассчитанное с помощью модели (1) – (3).

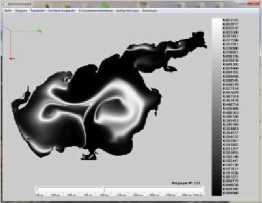
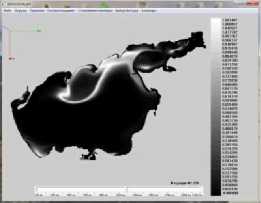
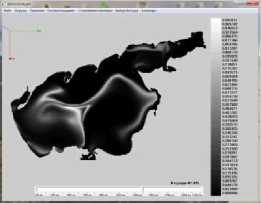
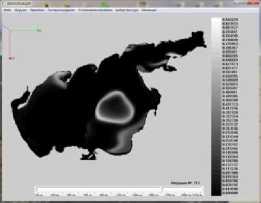
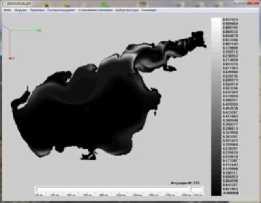
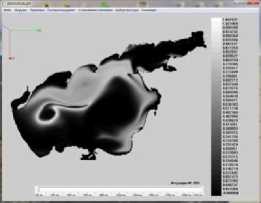
Рис. 5. Распределение концентрации фитопланктона в различные моменты времени

Рассчитанные при различных ветровых ситуациях концентрации загрязняющих веществ и планктона принимались к рассмотрению, если относительная погрешность не превышала 30%.

Заключение

На основе экспедиционных исследований выполнена первичная верификация модели экосистемы Азовского моря. Реализована задача моделирования и прогноза состояния водной экосистемы Азовского моря в условиях антропогенного воздействия и всестороннего изучения уникального водного объекта, который в силу своей мелководности в значительной степени подвергается антропогенному влиянию.

С помощью модели ЭВ (1) – (3) могут быть описаны процессы ассимиляции NH ₄ , нитратредукции (денитрификации), окисления H ₂ S , сульфатредукции, нитрифика-ции,окисления и восстановления марганца аммонификации, а также можно изучать механизм условий формирования заморов, прогнозировать изменения кислородного и биогенного режимов в мелководном водоеме. При построении модели были параметризованы процессы биогеохимических циклов химических элементов, ответственных за трансформацию аэробных условий в анаэробные [2].

Созданный программный комплекс объединяет математические модели и базы экологических данных, с помощью разработанного комплекса были изучены условия, при которых мелководные водоемы подвергаются эвтрофитрованию.

Отличительными особенностями разрабатываемых алгоритмов, реализующих поставленные гидробиологические модельные задачи, являются: высокая производительность, достоверность и точность получаемых результатов. Высокая производительность достигается за счет использования эффективных численных методов решения сеточных уравнений, реализованных на параллельных вычислительных системах в реальном и ускоренном масштабах времени. Достоверность достигается за счет учета определяющих физических факторов, таких как: стоки рек, испарение, сила Кориолиса, сложная геометрия береговой линии и дна водоема, турбулентный обмен, трение о дно и ветровые напряжения, динамическое перестроение расчетной области, а также за счет учета отклонения значения поля давления от гидростатического приближения. Точность достигается применением подробных расчетных сеток, учитывающих степень «заполненности» расчетных ячеек, а также отсутствием неконсервативных диссипативных слагаемых и нефизичных источников (стоков), возникающих в результате конечноразностных аппроксимаций.

Было проведено сравнение работы созданного программного комплекса, реализующего разработанные сценарии развития экологической обстановки в Азовском море с использованием численной реализации модельной задачи эвтрофикации вод мелководного водоема, с подобными работами в области математического моделирования гидробиологических процессов.

Анализ показал, что в результате разработки программного комплекса удалось повысить точность прогнозов изменения концентраций загрязняющих веществ, фито- и зоопланктона в мелководном водоеме на 10 – 15% в зависимости от решаемой модельной задачи водной экологии.

Работа выполнена при частичной финансовой поддержке Задания № 2014/174 в рамках базовой части государственного задания Минобрнауки России, а также при частичной финансовой поддержке РФФИ по проектам № 15-01-08619, № 15-07-08626, № 15-07-08408.