Математическое моделирование процессов нагрева и охлаждения колбасных изделий

В настоящее время уделяется повышенное внимание качеству тепловой обработки молока в условиях малых хозяйств и молочных ферм, зависящему от способов и режимов воздействия на исходное сырье, а также затратам энергии, необходимым на реализацию указанного процесса.

Модельное представление влияния условий термической обработки молока в установке инфракрасной (ИК) пастеризации на характер получения продукта с заданными показателями качества позволяет глубже понять и оценить основные физические закономерности протекания данного процесса.

Рассматривается нагревательный элемент для молока, состоящий из ряда последовательно соединенных кварцевых сферических колб, на наружной поверхности которых нанесен металлический токонесущий слой.

Нагревание молока осуществляется за счет пропускания электрического тока через токонесущий слой.

Поскольку линейное сопротивление токонесущего слоя (на единицу длины накала) в узкой части больше, чем в широкой, тепловыделение и температура токонесущего слоя в узкой части также будет больше, чем в широкой, поэтому нагревание молока при прохождении через нагревательный элемент осуществляется в осциллирующем режиме, что обеспечивает максимальную сохранность термолабильных веществ, содержащихся в молоке [1].

Бабенко М.С., Жучков А.В., 2013

Кроме того, в каналах переменного сечения коэффициент теплоотдачи к жидкости в 1,5-2 раза больше, чем в канале постоянного сечения [2], что позволяет выполнить конструкцию более компактной.

В каждой колбе происходит циркуляционное перемешивание молока, что приводит к дополнительному увеличению коэффициента теплоотдачи в узкой зоне соединения колб, а также более равномерн ому инфракрасному облучению молока.

Рассмотрим процесс нагревания молока в отдельном шарообразном нагревательном элементе (рисунок 1).

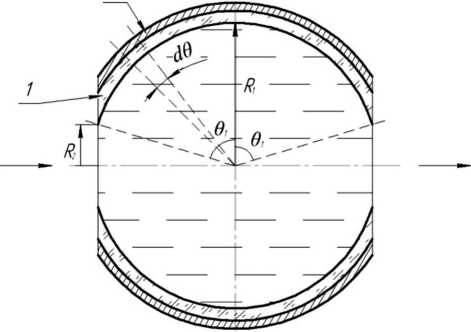
Рисунок 1 - Секция нагревательного элемента:

1 – кварцевая шарообразная оболочка; 2 – токонесущий слой

Задачу рассматриваем в сферической системе координат. Полагая задачу осесимметричной, а также полагая малое повышение температуры в каждой секции (не более 3-5°С), можно считать, что температура токонесущего слоя зависит только от угла 9. Предельные значения этого угла:

0! = arc cos (R^), (1) где R1 - внутренний радиус нагревательного элемента; R2 - радиус соединительного отверстия.

Выделим кольцевой элемент токон есущего слоя dO (рисунок 1) и определим его электрическое сопротивление в рабочих условиях:

dR э = р эо • [1 + « r (Т — Т о )] • ^R^, (2)

R1LOdУ Оэ где рэо - удельное электрическое сопротивление токонесущего слоя при температуре То; aR - температурный коэффициент сопротивления токонесущего слоя; Т - рабочая температура токонесущего слоя; 5э - толщина токонесущего слоя.

Мощность электрического тока в элементе d0:

dN = I2dR э,             (3)

где    I- величина тока.

C учетом (2) получим:

dN = A • [1 + « „ (Т-Т , )]^.(4)

где А = ^                     (5)

⁰ э

В соответствии с определением, величина A равна мощности тока в токонесущем слое толщиной 5_э, длина и ширина которого составляют по 1 метру при температуре Т о . В дальнейшем эту величину будем называть приведенной мощностью.

Поскольку при эксплуатации пастеризатора мощность тока N известна (измеряется приборами), величина A может быть определе на из условия нормировки:

N = j5/[1 + « r (Т-Т о )] ^,    (6)

^А = J ^ ¹ [1+a_R (Т-Г_о)]     ’         ⁽⁷⁾

J-У1«-     лч о , J_COS0

Если электросопротивление токонесущего слоя не зависит от температуры (a_R = 0), то из (7) следует:

N

^A = _ln i+sine₁ ,             ⁽⁸⁾

1-sin 61

В противном случае интеграл в знаменателе (7) определяется письменно после определения распределения температуры токонесущего слоя Т(0).

Уравнение теплового баланса для элемента токонесущего слоя d0имеет вид:

^dN = ^[ « воз ^(Т — ^Т воз ) + °Е воз ^{(у 4 — Т} воз ) +

^+км, ^{(Т —} Т, ^{) +} « , .^Т_:; )] -dF, ⁽⁹⁾ где а _воз - коэффициент теплоотдачи от токонесущего слоя к воздуху; Т_воз - абсолютная температура воздуха; о - постоянна Стефана-Больцмана (о = 5,67^10^-8 Вт/м²К⁴); Е_воз - степень черноты токонесущего слоя со стороны воздуха; к_м = _5с ¹ ₁ - коэффициент теплопередачи на участке «токонесущий слой - молоко»; 5_с - толщина стенки колбы; Л_с - коэффициент теплопроводности материала колбы; а_м - коэффициент теплоотдачи от внутренней поверхности колбы к молоку; Е_м - степень черноты токонесущего слоя со стороны молока; Т_м - абсолютная температура молока.

dF = 2^R2 cos 0d0,    (10)

здесь dF - элементарная площадь участка.

Приравнивая (4) и (9) с учетом (10), по- лучим:

[1 + « r (Т —Т о )]

А--—---d0 = cos(0)

= ^[ « воз ^{(Т — Т} воз ) ^{+ ОЕ} воз ^{(т4 — Т} воз ) ⁺ к_м (Т — Т_м ) + ое м (Т — Т 4 )] • 2nR 2 cos 9d9, (11)

или после преобразований:

А- [1 + « r (Т —Т о )]    =

2^R 2 cos² (0)

= « воз ^{(Т — Т} воз ) ^{+ ОЕ} воз ^{(т4 — Т} воз ) ⁺

+ к , (Т ^— У . ) ^{+ ОЕ} . ^{(Т —}С 1,          <12)

Коэффициент теплоотдaчи от внутренней поверхности колбы определяется в зависимости от режима течения молока [3].

При ламинарном режиме (Re < 2300):

Nu = 0,15Re °, ³²Pr °, ³³(GrPr) °, ¹,(13)

При турбулентном (Re > 2300):

Nu = 0,021Re °, ⁸Pr °, ⁴³,      (14)

где Nu = ^ м -^ ср   - число Нуссельта;

а _м - коэффициент теплоотдачи к молоку в трубе постоянного сечения; d _ср = R₁R₂ - средний диаметр канала; Л _м - теплопроводность молока; Re = —ср - число Рейнольдса для молока; ^V м

Pr = ^{V м} - ^{м р м} - число Прандтля для молока; с_м - теплоемкость молока; р _м - плотность молока; Gr = ^V^ ^ _м (Т с — Т _м ) - число Грасгофа для молока; д = 9,81 м/с² - ускорение свободного падения; ^ _м - температурный коэффициент расширения молока; Т с - температура внутренней поверхности колбы.

Значение найденного коэффициента теплоотдачи а_м корректируется с учетом волнообразного сечения канала:

Число Прандтля для молока определяет

ся по формуле:

Рг

ʹʹ

а м   ° а м,

У м "^см *^Р м

Л м    '

Коэффициент теплоотдачи вычисляется для

где    £' = 1,5^2 [2] - поправка, учитыва- ющаядополнительную турбулизацию потока.

Суммарный тепловой поток от токонесу

щего слоя к молоку определяется выражением:

Q М = Й^ М (Т - Т м ) + ае м (Т - Т 4 )] • 2^R₁ cos 9d9,        (16)

Общее тепловыделение в токон есущем слое равно его электрической мощности. При заданной приведенной мощности А, электри

ламинарного Л л и турбулентного Л т режимов.

Истинный коэффициент теплоотдачи выбирался в зависимости от числа Рейнольдса.

Непосредственное использование формулы (13) для расчета коэффициента

теплоотдачи а л не представляется возможным, поскольку в число Грасгофа входит неизвестная температура внутренней поверхности колбы Т_с . Ее значение

ческая мощность N равна:

N = А • J ^ ^“"'Т- о ) d9.    (17)

^J-^ i cos(0)

КПД нагревательного элемента:

Л = ^.               (18)

Конечная температура молока на выходе из колбы

предварительно определялось численными

"       ТЪ_

^{Т Т}   с м а „•

Важнейшим параметром пастеризатора,

определяющим качество продукта, является температура внутренней поверхности колбы Т с . При чрезмерно большом ее значении про

решениями уравнения:

д = Л л (Т с )(Т с -Т м )   ,       (27)

где д ~ — - удельный тепловой поток; F

F = 4hR 1 • sin 9₁ - площадь поверхности токонесущего слоя.

Коэффициент теплоотдачи при турбулентном режиме определяется непосредственно по формуле (14).

Окончательное значение коэффициента

исходит пригорание молока, разложение термолабильных веществ.

Температура внутренней поверхности Т с определяется из условия теплового баланса

для конвективных тепловых потоков: к м • (Т - Т м ) = а м (Т с - Т м ), _т _ _т     к м -(т-Т м )

^Т с    ' м +             .

^u м

Алгоритм машинного расчета процесса инфракрасной пастеризации молока реализуется следующим образом.

Определяются предельные значения угла

9₁ по формуле (1). Ориентировочное значение электрической мощности N определяется по формуле:

N = А- ln ^1+sinS1 .             (22)

1-sinS1                v 7

Средний диаметр канала определяется по формуле:

теплоотдачи определяется в зависимости от числа Рейнольдса:

'   (а л - приRe < 2300

^{а м}  (а т - приRe > 2300    ⁽²⁸⁾

с последующей корректировкой по формуле (15).

Температура токонесущего слоя Т(9) определяется путем численного решения уравнения (12). При этом предварительно рассчитывается коэффициент теплоотдачи для участка «токонесущий слой - молоко» к_м по формуле:

к м = ^          (29)

Лс Л м

Численным интегрированием уравнения (17) определяется мощность тока N для заданной приведенной мощности А.

Определяется тепловой поток от токоне

сущего слоя к молоку численным интегрированием уравнения (16). По формулам (18), (19) определяются КПД нагревательных элементов

d ср = R i + R₂.         (23)

Средняя скорость по формуле:

V =

молока определяется

пастеризатора и конечная температура молока при прохождении одной колбы.

Для оценки вкладов конвективной и лучистой формы передачи теплоты определяются удельный конвективный, лучистый и суммар

4G м ^^ ср "Р м

ный тепловой потоки к молоку:

Число Рейнольдса для молока определяется по формуле:

Re =     .             (25)

^v м

q мк = к м (Т-Т м ), (30) q мл = а° м (Т-Т м ), (31) ^q м = ^q мк ^{+ q} мл .. ⁽³²⁾

Последней определяется температура внутренней поверхности колбы по формуле (21).

На рисунках 2, 3 приведены результаты моделирования пастеризатора молока при следующих значениях      параметров:

R ^ = 0,04м;      R₂ = 0,02 м ;      8 с = 0,001 м ;

Л с = 2,4 Вт К ; Т в = 293 К ; Т_м = 293 К ; а в = 10 Вт ; £₆ = 0,1; е_м = 0,9; а = 5,67 • 10 " ⁸ Вт^ ;

м 2 К                                       м 2 к aR = 0,25 • 10-3 к (покрытие из нихрома); А = 1500Вт; G„ = 1 к;; рм = 1030 -Т; см = 3900ДжК; Лм = 0,56 Вт К; vM = 0,5 • 10“6 —; кг       м          м       м                с

Р = 4,5 • 10 ~ ⁴ ^

К

А также рассчитаны важнейшие     параметры:

к_м = 1397 мВт ; n = 4150 Вт ; р = 0,992; Т м = 294,1 К .

следующие Вт ам = 10 м 2 К;

Q m = 4116Вт;

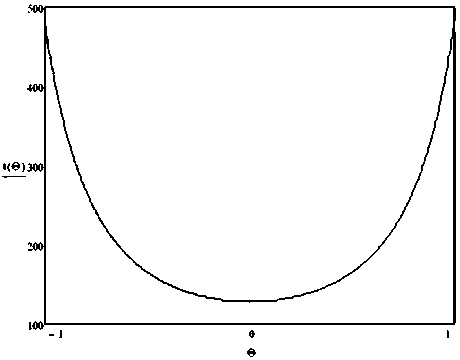
Рисунок 2 - Распределение температуры токонесущего слоя

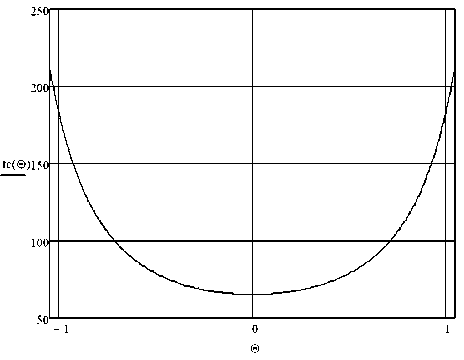
Рисунок 3 - Распределение температуры на внутренней поверхности колбы

С учетом того, что скорость молока здесь существенно выше, чем в широкой части, время высокотемпературного нагрева молока мало по сравнению с общим временем прохождением молока через колбу.

Увеличение мощности тока приводит к резкому увеличению температуры внутренней поверхности колбы. На рисунке 4 показано распределение t с при А = 3000 Вт (N = 8728 Вт ). Остальные параметры неизменны.

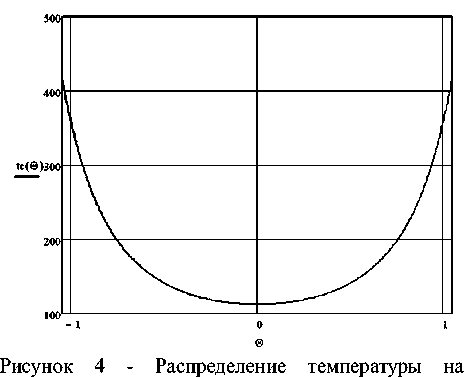
внутренней поверхности колбы при А = 3000 Вт ( N = 8728 Вт )

Если режим течения в устройстве ламинарный, то температуры токонесущего слоя и внутренней поверхности колбы получаются недопустимо высокими, что вызовет пригорание и разложение термолабильных веществ.

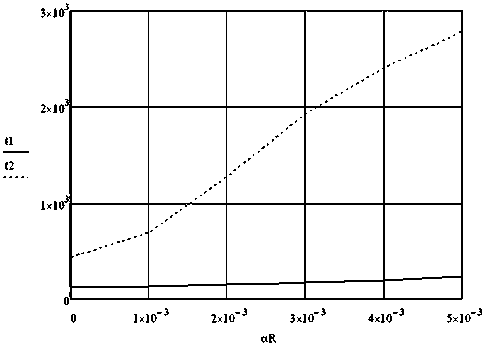
Рисунок 5 - Зависимость температуры токонесущего слоя от температурного коэффициента сопротивления материала

На температуру токонесущего слоя существенно влияет температурный коэффициент сопротивления материала. На рисунках 5 и 6 показаны соответствующие зависимости для токонесущего слоя и внутренней поверхности колбы. Индекс 1 относится к наиболее широкой части колбы, индекс 2 - к наиболее узкой (входному сечению).

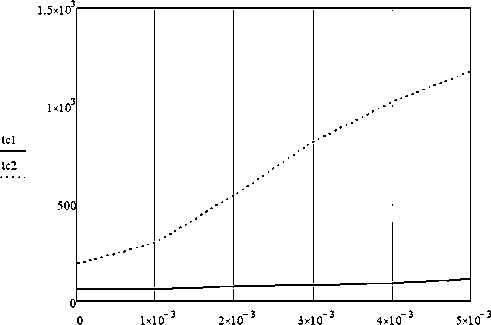
«R

Рисунок 6 - Зависимость температуры внутренней поверхности колбы от температурного коэффициента сопротивления материала

При одинаковой электрической мощности температуры токонесущего слоя и внутренней поверхности колбы существенно зависят от материала токонесущего слоя, в то время как в широкой части они несколько уменьшаются.

Перегрев узкой части колбы можно предотвратить увеличением входного радиуса колбы R2. На рисунках 7 и 8 показаны зависимости температур от радиуса R2 при aR = 0,25 • 10-3 7:, N = 2000 Вт. Температуры К во входном сечении t2 и tс2 существенно уменьшаются при увеличении радиуса R2, а температуры t1 и tс! несколько увеличиваются. Таким образом, увеличение радиуса R2 с одной стороны приводит к уменьшению максимальной температуры, с другой - к уменьшению амплитуды колебаний температуры нагревателя в осциллирующем процессе подогрева.

Результаты математического моделирования процесса пастеризации позволяют сделать следующие выводы.

Эффективная пастеризация молока возможна только при турбулентном режиме течения через нагревательные элементы пастеризатора. В случае ламинарного режима происходит чрезмерный перегрев нагревательных элементов и, как следствие, пригорание молока во входном сечении, разложение термолабильных веществ.

При работе данного пастеризатора реализуется осциллирующий режим подогрева молока. Максимальная температура токонесу- щего слоя и внутренней поверхности колбы наблюдается в наиболее узком (входном сечении), минимальная - в наиболее широком.

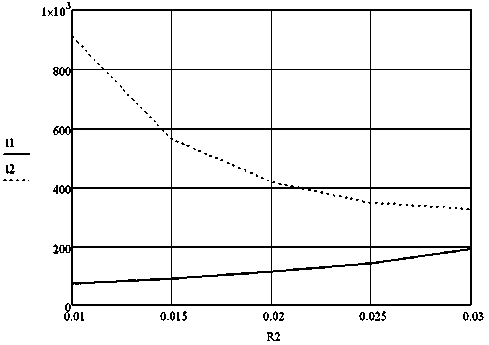
Рисунок 7 - Зависимость температуры токоне-сущего слоя от радиусавходного сечения

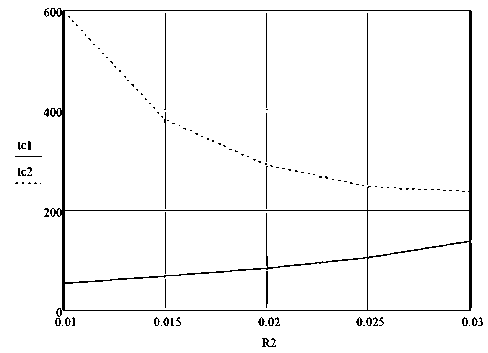
Рисунок 8 - Зависимость температуры внутренней поверхности колбы от радиуса входного сечения

Наличие циркуляционных контуров в колбах приводит к интенсивному перемешиванию молока, более равномерному ИК-облучению.

Максимальная температура в наиболее узком сечении пастеризатора зависит главным образом от электрической мощности тока, радиуса наиболее узкого сечения, температурного коэффициента сопротивления токонесущего слоя. Токонесущий слой желательно выполнять из материалов с малыми значениями температурного коэффициента сопротивления (манганин, нихром).

Амплитуда колебаний температуры токонесущего слоя и внутренней поверхности колбы зависит от соотношения радиусов R ^ и R 2 и может регулироваться их значениями в достаточно широких пределах.

ВестникВГУИТ, №4, 2013