Математическое моделирование процессов при электродуговом синтезе углеродных нанотрубок

Ряд особенностей электродугового синтеза углеродных нанотрубок (УНТ) (наноразмеры получаемого продукта, быстротечность, малые размеры области реакции) усложняют эмпирические исследования и повышают актуальность применения средств математического моделирования.

Во многом определяющим результат данного технологического процесса является дей -ствие температуры. Данный факт повышает актуальность математического моделирования температурного поля в установке синтеза УНТ.

Моделирование теплопереноса при элек-тродуговом синтезе УНТ позволит определить роль температурного распределения в формировании депозитных фракций на катоде, выработать рекомендации по оптимизации процесса, а также влияние конструктивных параметров охлаждающего элемента на температурное распределение.

Расчетная схема электродугового синтеза УНТ и фуллеренов может быть представлена в следующем виде (рисунок 1).

Рисунок 1 - Расчетная схема процесса теплообмена

где T an , T kat , T os , T pl , T isp , T ohl , T 0 – температура анода, катода, осадка, плазмы, испарения, теплоотводящего элемента, окружающей среды соответственно; L an , L kat , L os , L pl , L isp , L ohl – расстояние от начала координат до правой границы ан ода, катода, осадка, плазмы, испарения, левой и правой границы теплоотводящего элемента соответственно;

R, R ohl , R gel – радиус электродов, теплоотводящей компоненты и рассматриваемого объема гелия соответственно.

Проведенный анализ процесса элек-тродугового синтеза УНТ позволил выделить основные способы передачи тепла в рассматриваемой системе. Было сделано допущение о том, что механизм передачи тепла в плазме – конвективная теплопроводность с объемным

источником тепла; в аноде, катоде, осадке, теплоотводящем элементе - теплопроводность; в буферном газе - конвективная теплопроводность [1,2, 3]. Влияние излучения плазмы и излучения нагретых электродов не учитывалось. Плазма, осадок и рассматриваемый объем гелия имеют форму цилиндра, учитывается изменение подвижной границы формирования депозита на катоде и испарения анода во времени. Теплофизические параметры приняты постоянными.

Помимо этого полагалось, что в течение процесса графитовые электроды сохраняют постоянство плотности и однородность.

На основе принятых допущений была синтезирована математическая модель теплообмена при синтезе УНТ, учитывающую отвод тепла из зоны испарения анода. В основе модели лежат уравнения теплопроводности [4].

С учетом принятых допущений и оценок исходная система уравнений теплообмена в операторной форме примет вид:

о C • ^д an = к • f-— an + fl ^д an + -—an -1 ^p an C an ~      ann ⁽ _ 7 ^{+ (11} ' )         ⁺ - 7 )

д t            д r2             д r     дz n С    д Tkat   ,     ,д2 Tkat           д Tkat

Pkat ' Ckat '        = kkat • ( ■■ 2 + (1/r) •    ---+ д t             д r 2             д r

. д ² T ka _t )

д z ²

n с    д T ohi   ,      д ² T ohi           д T ohi

P ohl • C ohi • —T— = k ohi • ⁽ ■ 2 ^{+ (1/ r} ) • --- ⁺ д t             д r ²               д r

, д ² T ohi )

д z ²

Ps • Cos • — = k0s • ( os os              os д t

)

д z

os + (1/r) • д r 2

д T os + д r

г I ^д Tgel ^P g^el ^ ^C gel ^ I д t   ⁺ u

gel r

^д T gel ₊ u д r

-k ( kgel  ( дr2

. ^д T gel

+ (1/ Г)--— + д r

gelz д 2 Tgel дz 2

^{д T} gel д z

-)

I д T_pl

Ppi • Cpi 'I ~~дГ +

pl r

^д T Pi ₊ д r

u pl z

д T pi д z

д ² Tpi

= kpi • ( "ТГ д r

д T,/

+ (1/ r ) • -pl - + д r

д ² T„/

) + Q д z

где k an , k kat , k os , k pi , k gel, k ohl - теплопроводность анода, катода, осадка, плазмы, ТЭ соответственно; P an , P kat , P os , P pi , P ohl - плотность анода, катода, осадка, плазмы, ТЭ соответственно; C an , C kat , C os , C pi , C ohi - удельная теплоемкость анода, катода, осадка, плазмы, ТЭ соответ

ственно; u_r , u_z - составляющие вектора скорости вдоль осей координат; Q - объемное тепловыделение; T an , T kat , T os , T pi , T ohi - температура анода, катода, осадка, плазмы, ТЭ соответ

ственно; п - динамическая вязкость гелия.

В начальный момент времени температура всех компонент рассматриваемой системы принимается равной температуре окружающей среды^{: T} 0 gel = ^T 0 an = ^T q kat = ^T ) os = ^T 0 pl = ^T 0 .

Граничные условия в рассматриваемой системе координат имеют следующийй вид [5,6].

Для катода:

T kat l z = 0 = T 0

k kat

1 , kkat

д T kat д z д T kat д r

д T kat д r

r = 0

z l kat

r = R

= 0

Для осадка:

t    д Tkat kkat дz

^TosV = l os ( t )

к   - Tos.

kos д r

д Tos	r = 0
д r

= 0

Tan

= k ^^

os ~ дz

α gel (T kat

^z = ^l kat

—

z l kat

■^T 0 ) L. R

-k -Tos kos дz

= Tpl| z = los (t)

^z = l kat

r = R

Для анода:

= ^a gsl^(Tos  ^T 0 )

¹ r = R

^z = ⁱ isp ⁽t)     ^Tlsp\z = l i_Sp (t)

Tan

^T 0

kan z=lan д Tan д r

д Tan
д r	r = 0

= 0

r = R

= ^agei^(Tan  ^T 0 )

r = R

Для плазмы:

T pl

T pl

kPi

^z = ^l os ( t )

^z = l isp ( t ) д T pi

д T pi д r

д r

r = 0

= T I z=los (t)

= T I lsp|z=lisp (t)

= a

r = R

r = R

= 0

Для теплоотводящего элемента:

k ohl

d T ohl d z

= k.

z = L ohi (t)

k ohl

^

d T ohl d z

^z L an

=k

d Tan an dz

⁵ T gel

^gel   d z

z = L ohl (t)

^z = L an

d T ohl d r d T ohl d r

= 0

^r = R ohl

=0

r = 0

Для буферного газа:

T , ge^l z = 0

Tgel z = L,

= Tо

= Tо

T gel

gel

r = R gel

= Tо

^d T gel d r

= 0

r = 0

В качестве функций, описывающих подвижные границы, используются следующий выражения.

Для границы плазма-депозит:

^L os ^(t) = L kat + a ■ t , Для границы анод-плазма:

L isp (T ( t ), t) =

L pi + ( a1 ■ T ( t )^ + b1 ■ T ( t ) +

d) ■ t

Функции (8)-(9) получены, исходя из экспериментальных данных. Коэффициенты а, al, bl, c1 определяются экспериментально.

Решение системы дифференциальных уравнений (1) с граничными условиями (2)-(7) проводилось численно с использованием метода декомпозиции области, основанном на конечно-элементной аппроксимации. Алгоритм метода представлен на рисунке 2. Для решения рассматриваемой задачи используется четырехузловой изопараметрический ко-

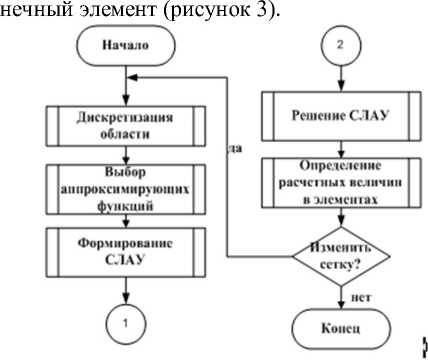
Рисунок 2 - Алгоритм метода конечных элементов

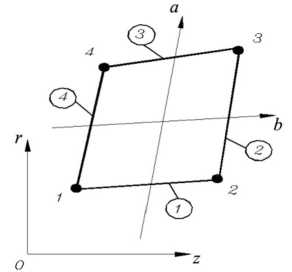
Рисунок 3 - Четырехузловой конечный элемент

Температура T аппроксимируется во всей области конечного элемента функциями форм следующего вида:

T (a, b )=Z Ni(a, b Ti =[N (a, b )]{t(e)} i=1                               ,         (10)

где N i ( a , b ) - функции форм; { t ^{( e} ) } - вектор

узловых температур конечного элемента.

Решение системы нестационарных дифференциальных уравнений теплопроводности (1) с граничными условиями (2)-(7) заменим другой задачей, т.е. найдем распределение температуры T ( t , r , z ), минимизирующее следующие функционалы:

J, = 1J к, i                        i

² V

V

_ х 2      ,   _ х 2

d T I    , ( 8 T I

—^L I + ki I —^L I 8 r )       V 8 z J

—

— 2 T I Q_t — p c, I ^ T ² + u_r ^T- + u_z i i ii             r            z

V d t ¹ d r

d T i |

8 z J

) rdV

+

J

+ Z j rq ij T i dA + Z ¹ J h_lkr ( T i — T 0 )² dA j S             k ² S

Конечно-разностное уравнение для определения искомой температурной зависимости имеет вид:

-M + K { T t +T } = { P t +T } + [ M 1- { T t } — { T t } |      (12 )

. T J                      \ T J

Построенная математическая модель позволяет исследовать влияние параметров теплоотводящего элемента (ТЭ) на температурное распределение.

Важным конструктивным параметром теплоотводящего элемента является его радиус. Исследование влияния радиуса теплоотводящего элемента на ширину зоны формирования УНТ показало, что для рассматриваемой системы наибольшее значение ширины зоны

формирования УНТ достигается при радиусе вания УНТ показал, что для рассматриваемой системы наибольшее значение ширины зоны

ТЭ 0.2 - R ^ 0.4 - R, где R - радиус анода.

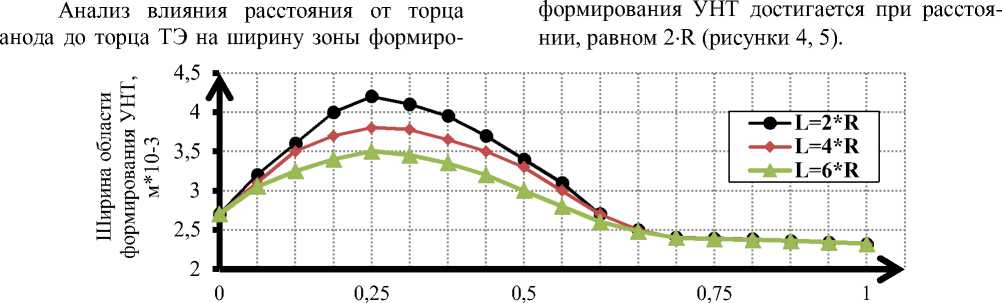
Относительный радиус теплоотвода Rohl/R

Рисунок 4 - Зависимость ширины зоны формирования УНТ от радиуса ТЭ при различных расстояниях до торца ТЭ

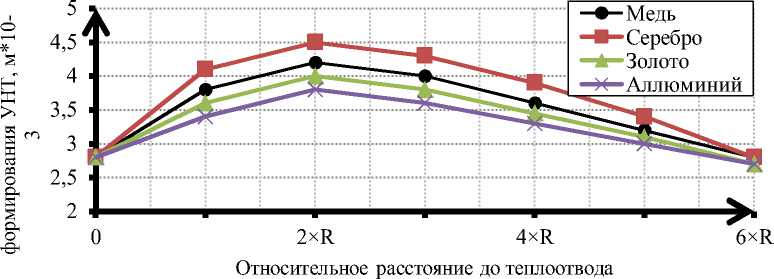
Рисунок 5 - Зависимость ширины зоны формирования УНТ от расстояния до торца ТЭ при различных материалах ТЭ

При разработке технологического оборудования для реализации синтеза УНТ элек-тродуговым методом возможно использование теплоотводящих элементов с различной теплопроводностью. Был проведен анализ влияния материала ТЭ на ширину зоны формирования УНТ. В качестве материала ТЭ рассматривались металлы с наибольшей теплопроводностью. Для рассматриваемой системы с увеличением теплопроводности материала эффек- тивность отвода тепла возрастает (рисунок 6). Однако при разработке технологического оборудования следует учитывать стоимость данных материалов.

Таким образом, исследование распределения параметров при электродуговом синтезе УНТ позволяет лучше понять особенности процесса и выявить условия, способствующие расширению области формированияУНТ.

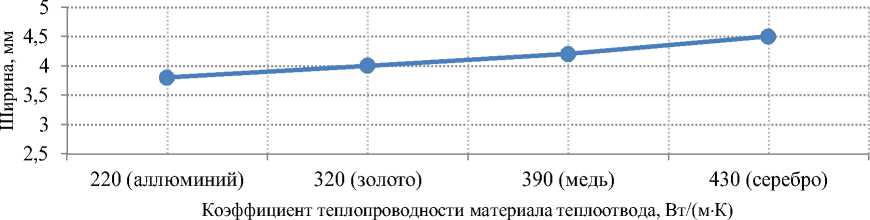
Рисунок 6 - Зависимость ширины зоны формирования УНТ от материала ТЭ

Полученные в результате исследований зависимости распределения параметров при электродуговом синтезе УНТ соответствуют общим представлениям о процессах, происходящих в электродуговом разряде. При этом значение теплового поля влияет на состав углеродного депозита, содержащего нанотрубки.

Результаты исследований создают предпосылки для создания комплекса прикладных программ для имитационного моделирования процессов при электродуговом синтезе углеродных нанотрубок.