Математическое моделирование процессов тепломассообмена в двухфазном контуре терморегулирования с капиллярным насосом

В настоящее время прослеживается тенденция к увеличению тепловой мощности, выделяемой радиоаппаратурой на борту космических аппаратов (КА), поэтому повышается роль одной из важнейших систем обеспечения функционирования КА - системы терморегулирования (СТР). В классических СТР используются однофазные жидкостные контуры, в которых теплопередача осуществляется за счет теплоемкости теплоносителя. Разработка двухфазных тепловых контуров, использующих скрытую теплоту фазового перехода, позволит снизить расход рабочего тела, вес СТР и увеличить эффективность тепло переноса. Экспериментальный образец двухфазной СТР с механической прокачкой теплоносителя был успешно испытан на российском сегменте международной космической станции «Альфа» [1].

Перспективным направлением развития СТР является двухфазный контур с капиллярным насосом (ДФК КН), который отличается полной автономностью, отсутствием энергопотребления и движущихся механических частей, меньшей массой и более высокой надежностью [2]. Основным элементом таких систем является капиллярный насос, который определяет эффективность работы контура в целом, поскольку именно в нем происходит парообразование и за счет капиллярных сил, действующих в его объеме, обеспечивается циркуляция теплоносителя в контуре. Проектирование ДФК КН затруднено вследствие сложности и неопределенности механизмов парообразования, межфазового взаимодействия и передачи теплоты в гетерогенных средах. Поэтому разработка конструкции двухфазных контуров терморегулирования возможна на основе развития математических моде лей, позволяющих выработать оптимальные технические решения и прогнозировать эксплуатационные характеристики при различных условиях работы. В данной статье представлены две сопряженные математические модели, одна из которых предназначена для расчета параметров теплоносителя в паровом и жидкостном трактах контура, другая - для определения распределенных характеристик в пористой структуре капиллярного насоса.

Рассмотрим явления, протекающие в ДФК КН, схема которого представлена на рис. 1. Процесс тепломассопереноса в контуре можно описать следующим образом. Тепловой поток подводится на внешнюю поверхность теплообменника, который совмещает в себе функцию капиллярного насоса. В объеме КН жидкий теплоноситель испаряется, поглощая теплоту. Силы поверхностного натяжения препятствуют проникновению пара вглубь пористой структуры (ПС), поэтому газообразный теплоноситель по паровому тракту поступает в конденсатор, где снова превращается в жидкость, выделяя энергию. Образовавшаяся жидкость за счет капиллярных сил, действующих в ПС, возвращается в теплообменник. Таким образом, в контуре происходит циркуляция теплоносителя и осуществляется перенос теплоты. Характеристики процесса теплопереноса зависят от тепловой нагрузки, тепло физических свойств теплоносителя, параметров пористой структуры, сечения и протяженности парового и жидкостного трактов контура и т. д.

Расчет параметров теплоносителя в контуре. Теплофизическая модель двухфазного контура основывается на законах гидродинамики и теплообмена, применяемых как к жидкостному, так и к паровому тракту. Начальной точкой расчета являются параметры теплоносителя в конденсаторе. Здесь значение температуры Т рассчитывается по уравнению теплового баланса, которое записано с учетом суммарной мощности тепловыделения контура О и условий теплообмена с окружающей средой:

.....        0 = 8^5,        ₍1) где ст - постоянная Стефана-Больцмана; s, S- коэффициент черноты и площадь поверхности радиатора, соответственно. Величина давления р в конденсаторе рассчитывается по кривой насыщения теплоносителя для температуры Т.

капиллярный насос

- - жидкость конденсатор

Рис. 1. Принципиальная схема двухфазного контура терморегулирования

Значения давления жидкости на входе в капиллярный насос р и пара на выходе из насоса/> определяются с учетом потерь давления вследствие вязкостного трения как в жидкостном, так и в паровом трактах контура:

f dp Л т p™ = pxxL^ (2)

V dl

( dp Л т

P™t= А+Нг X       (3)

V dl у ₂

где L - протяженность трактов; индексы 1 и 2 относятся к паровому и жидкостному трактам соответственно.

Величина градиента давления в установившемся режиме течения теплоносителя определяется выражением [3]

^dp А = 12dE          (4)

где ц - коэффициент динамической вязкости; m - массовый расход жидкости в данном сечении;/- коэффициент гидравлического сопротивления; Re - число Рейнольдса; А - площадь поперечного сечения тракта; R - радиус тракта; р - плотность теплоносителя; i = 1 для параметров пара и / = 2 для жидкости.

Значения / и Re зависят от параметров потока. При условиях, когда число Рейнольдса меньше 2 300, а число Маха меньше 0,2 (для газа), течение можно рассматривать как ламинарное и несжимаемое. В этом случае для круглых каналов значение/ • Re = 16.

Расход теплоносителя m определяется величиной тепловой нагрузки О, удельными теплоемкостью с и теплотой парообразования г^ и зависимостью T_s(pY соответствующей кривой насыщения теплоносителя:

т=------.          (5)

Таким образом, распределение параметров в контуре зависит от мощности тепловой нагрузки, характеристик радиатора, свойств теплоносителя, протяженности и поперечных размеров трактов контура. Рассчитанные с помощью выражений (1)... (5) значения давления р и р_ои1 являются граничными условиями для моделирования процессов тепломассообмена в капиллярном насосе.

Математическая модель тепломассообмена в капиллярном насосе. Основным конструктивным элементом капиллярного насоса является цилиндрическая пористая вставка, которая имеет центральный внутренний канал для подвода жидкого теплоносителя и каналы для отвода пара (рис. 2). Тепловой поток подводится на внешнюю поверхность насоса, нагрев каркаса ПС происходит за счет теплопроводности. Жидкий теплоноситель под действием капиллярных сил движется к внешней поверхности, силы поверхностного натяжения не позволяют жидкости проникать в пароотводящие каналы, поэтому нагрев и испарение теплоносителя происходит в объеме ПС. Далее образовавшийся пар выходит в контур по пароотводящим каналам. Положение и форма фронта испарения теплоносителя, распределение температуры в ПС и значение температуры на поверхности зависят от геометрических параметров насоса, физических свойств материала пористой структуры и мощности тепловой нагрузки.

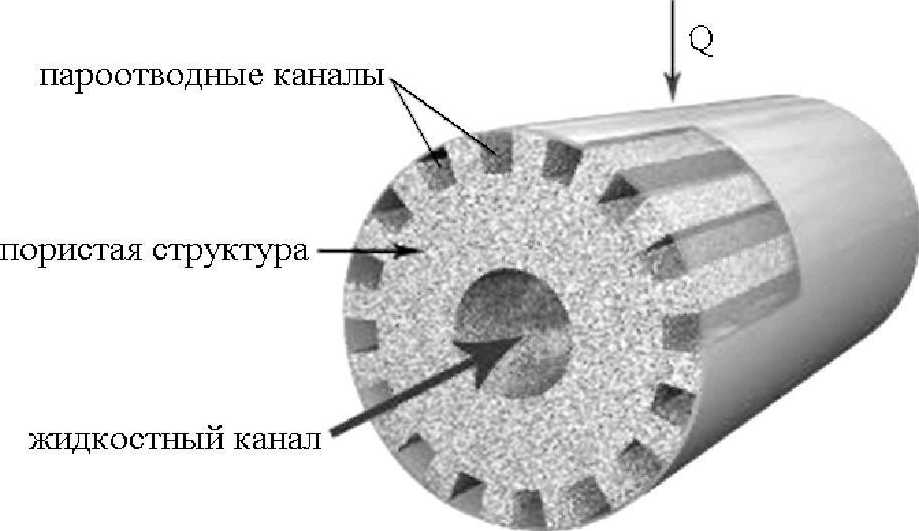
Рис. 2. Устройство пористой вставки капиллярного насоса

При расчете характеристик такой системы в математической модели учитываются теплообмен, основанный на механизмах теплопроводности и конвекции, взаимодействие жидкого и газообразного теплоносителя с ПС и фазовые превращения. Граничными условиями являются параметры, рассчитанные по разработанной ранее модели всего контура.

Для описания движения теплоносителя в ПС использованы двухмерные уравнения фильтрации в цилиндрических координатах г и 9:

У /oxY дг    ц/р/ дг)

Д Af. М^ф ч _{= ы}      (6)

г 50   ц^. d^ J ’ где f^C) - относительная проницаемость фазы при данной концентрации; az - вязкостный коэффициент сопротивления пористого материала; р. - коэффициент динамической вязкости; J-интенсивность межфазового мас-собмена; индексы z = 1 и z = 2 относятся к паровой и жидкостной фазам соответственно.

По решению уравнений (6) определяется поле давления теплоносителя в пористой структуре, на основе которого рассчитываются скорости обеих фаз. Согласно уравнениям Дарси, радиальные и угловые компоненты вектора скорости и и v вычисляются по следующим формулам:

№’М (бр цгРг <8г г цгРг

Для определения температурных полей решается двумерное уравнение энергии, которое включает слагаемые, отвечающие за теплопроводность и конвекцию:

ЭТ 1 д < , ЭТА рс— =--ГЛ— +

3/ г Эг\ 5г)/§\

1 э L этЛ’ г2 do) к

^к — СчРЛ "^^гРг^г) - z                 , 1 ЭТ

+(c1p1v1+c2p2v2)-—, г 30

где р, с, X - соответственно суммарные плотность, теплоемкость и коэффициент теплопроводности пористой структуры и теплоносителя.

На внешней границе для этих уравнений задаются условия

Эр ЭТ

— = 0 — = q/X .

Эг ’ дг

(Ю)

В центральном канале насоса заданы температура и давление, соответствующее состоянию жидкости на входе. В пароотводных каналах давление равно величине, рассчитанной по модели всего контура для пара на входе в паровой тракт.

В общем случае граница раздела «пар-жидкость» в пористой структуре не является стефановской, а имеет объемную структуру и занимает слой определенной толщины. Радиус мениска, разделяющего жидкость и пар в порах, может быть получен по выражению

(И)

Р1"Р2

где (У - коэффициент поверхностного натяжения теплоносителя. В пористой среде имеются поры различных размеров, поэтому согласно выражению (11), в объемной зоне фазовой границы поры, радиус которых R < R будут заполнены жидкостью, а в порах cR> R_m будет находиться пар. Толщина зоны фазовой границы задана функцией распределения пор по радиусам, теплофизическими свойствами теплоносителя и мощностью приложенной тепловой нагрузки.

При решении задачи Стефана теплоемкость фазового перехода с является 5-функцией на границе фазового перехода. В пространственной зоне испарения теплоем- кость распределяется на некоторый температурный интервал [Г- АТ, Т + АТ], соответствующий кривой насыщения разнице давления пара в порах различного размера. Зависимость с^Т) определяется законом распределения размера пор, который не всегда известен. В данной статье использована модельная синусоидальная функция (рис. 3).

По значению концентраций теплоносителя определяются относительные фазовые проницаемости для обеих фаз. Они зависят только от вида пористой структуры и ее насыщенности каждой фазой [4] (рис. 4). Обращает на себя внимание тот факт, что при малом содержании каждой из фаз в пористом каркасе ее относительная проницаемость равна нулю, т. е. данная фаза неподвижна. Физическое объяснение этого свойства состоит в том, что при малом содержании смачивающей фазы она собирается вокруг точек контакта частиц в виде защемленных жидкостных колец. Эти кольца изолированы друг от друга и не образуют непрерывной жидкой фазы в пористом материале, поэтому жидкость и неподвижна. По мере увеличения ее содержания кольца расширяются, сливаются и образуют непрерывную жидкостную фазу, после чего ее течение становится возможным.

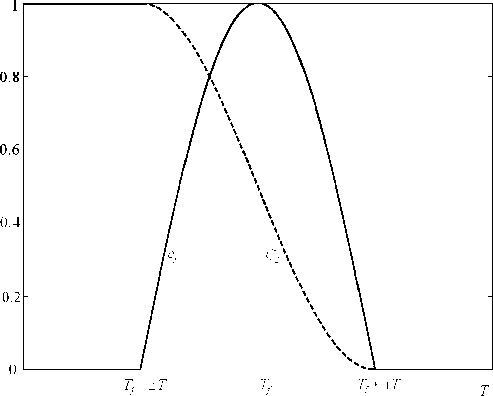
Рис. 3. Зависимости теплоемкости с . и относительной концентрации жидкой фазы С₂ от температуры в окрестности температуры фазового перехода T_f

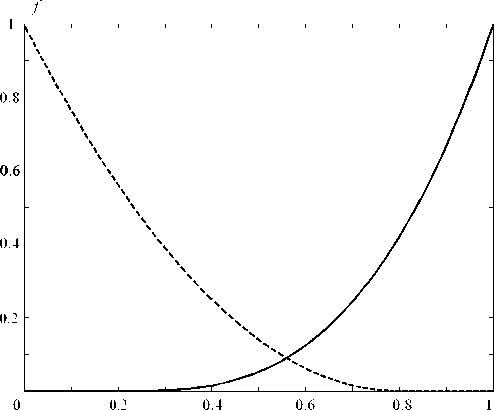
Рис. 4. Относительные фазовые проницаемости жидкости (сплошная линия) и газа (пунктир) в зависимости от насыщенности пористой среды жидкой фазой

Система уравнений (4)... (10) решается численно, дискретный аналог получен с помощью метода контрольно- го объема, при этом использована неявная схема аппроксимации со вторым порядком точности по пространству и времени [5]. Решение систем алгебраических уравнений проводится по итерационному методу Гаусса-Зейделя с верхней релаксацией.

Представленная математическая модель позволяет рассчитывать распределения концентраций теплоносителя в жидкой и паровой фазах, поля температуры, давления и скорости в ПС капиллярного насоса. В качестве теплоносителя рассматривается аммиак. Геометрические размеры задачи следующие: радиус капиллярного насоса 15 мм; радиус центрального жидкостного канала 2 мм; ширина пароотводных каналов 1 мм; высота 2 мм; расстояние между канавками 4 мм. Значения плотности теплового потока, поступающего на внешнюю поверхность насоса, q = 16 кВт/м².

Распределение концентрации жидкой фазы теплоносителя в градациях серого цвета отображено на рис. 5. При рассматриваемой плотности теплового потока область чистого пара примыкает к внешней поверхности ПС и пароотводящим каналам, а объемная зона фазового перехода, где преобладает пар (С2 < 0.5). расположена между каналами.

Как показывают результаты данного расчета, зона парообразования для рассматриваемой тепловой нагрузки находится вблизи внешней границы ПС. Приувеличении тепловой мощности зона раздела фаз перемещается вглубь насоса и происходит частичное осушение ПС. которое приводит к росту температуры на поверхности насоса. Математическая модель капиллярного насоса позволяет также исследовать зависимость рабочих характеристик насоса от конструктивных параметров и граничных условий.

1.550Е+0Е

1.533Е+0Е

1.517Е+0Е

1.500Е+0Е

1.483Е+0Е

1.467Е+0Е

1.450Е+0Е

1.433Е+0Е

1.417Е+0Е

1.400Е+0Е

1.383Е+0Е

1.3Б7Е+0Е

1.350Е+0Б

Рис. 6. Распределение давления пара, Па

1.000Е+00

9.167Е-01

8.333Е-01

7.500Е-01

БББ7Е-01

5.833Е-01

5. OODE-01

4.1Б7Е-01 З.ЗЗЗЕ-01

2.500Е-01

1.ББ7Е-01 8.333Е-02

0. ОБОЕ+00

Рис. 7. Поле температуры, °C

4.454Е+01

4.083Е+01

3.712Е+01

3.341 Е+01

2.Э6ЭЕ+01

2.5Э8Е+01

2.227Е+01

1.856Е+01

1.485Е+01

1.114Е+01

7.423Е+00

3.712Е+00

0.000Е+00

Рис. 5. Поле концентрации жидкой фазы теплоносителя £ (изолинии соответствуют значениям С2 = 0; 0,5; 1)

Наибольший градиент давления характерен для паровой фазы теплоносителя, когда пар в ПС движется с высокой скоростью, что и обусловливает большое гидравлическое сопротивление (рис. 6). Наоборот, изменение температуры по радиусу достаточно гладкое (рис. 7). поскольку перенос теплоты в насосе осуществляется равномерно по всему объему за счет теплопроводности каркаса ПС и конвекции теплоносителя. Максимальное значение температуры находится на внешней поверхности насоса; в окрестности пароотводящих каналов изолинии температуры искривлены; ближе к центру ПС они имеют форму правильных окружностей. влияние каналов здесь отсутствует.

Распределение давления в ПС определяет поле скоростей теплоносителя (рис. 8). Наибольшее значение скорости наблюдается в зоне основания канала, некоторая доля теплоносителя движется по дуге, поступая в пароотводящий канал через ее боковые стороны.

Распределения концентрации фаз. температуры, давления и скорости дают полное количественное описание процессов тепломассообмена в объеме капиллярного насоса.

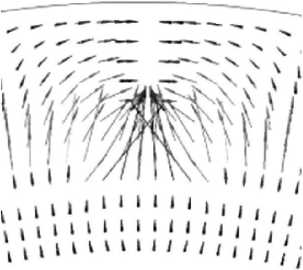
Рис. 8. Векторы скоростей пара в области пароотводного канала

Таким образом, представленные выше математические модели, предназначенные для исследования тепловых режимов двухфазного контура терморегулирования и капиллярного насоса, позволяют рассчитать все основные характеристики процесса теплообмена и определить предельные тепловые потоки, поступающие от бортовой аппаратуры в систему терморегулирования КА. Результаты моделирования могут служить основой для проведения оптимизации геометрических и теплофизических параметров капиллярного насоса и системы охлаждения в целом.