Математическое моделирование распространения ударной волны в гетерогенной среде с химическими превращениями в газовой фазе

Исследование процесса распространения ударных волн (УВ) в двухфазной гетерогенной среде имеет большое практическое значение, в частности, для разработки методов обеспечения работ в шахтах, тушения лестных пожаров и т.д.. Согласно [1, 2] лесной пожар представляет собой многостадийное явление, включающее в себя процессы прогрева лесного горючего материала (ЛГМ), их сушку и пиролиз с последующим горением газообразных и конденсированных продуктов пиролиза. На стадии пиролиза в газовую фазу поступают горючие газообразные вещества (угарный газ, метан), что обеспечивает возможность протекания в газовой фазе химических реакций окисления. Подрыв шнурового заряда взрывчатого вещества (ВВ) в определенном участке фронта пожара приводит к «выжиганию» продуктов пиролиза и прекращению распространения пожара [2].

Целью настоящей работы является математическое моделирование распространения цилиндрически расходящейся УВ в двухфазной гетерогенной среде с химически активной газовой фазой.

Постановка задачи

Следуя [3], запишем систему уравнений модифицированной модели «замороженной» газовзвеси в переменных Лагранжа в виде

1 da du dv σ dt ∂x ∂y , dni dt

E A g . j

du ∂p pd — - dX + fx’ dx dt — u’

dv ∂p pdt — - dy + fy ’ dy dt v’

dE dt

• pd ^{+ a} D ^(A E ^{, j} 'g j )’ j

E — rt ^(’), p = (7e// — i)pE, — ^n, i µi

Y.. -1+ [E (I ^E (

Здесь ρ – массовая плотность газовой смеси; p – давление смеси; u, v – x и y компоненты скорости смеси; a — 1/p - удельный объем; п г - молярно-объемная концентрация i-й компоненты смеси (моль/м ³ ); A j - стехиометрический коэффициент компонента смеси, где номер химической реакции указан верхним индексом в скобках, а номер компонента смеси нижним индексом; g ^{( j )} - скорость протекания j-й реакции (моль/(м ³ с)); E - удельная внутренняя энергия смеси, с учетом полного тепловыделения (поглощения) за счет химических превращений; c i – массовая концентрация i -й компоненты смеси (доля массы i -й компоненты в полной массе смеси малого элемента объема); µ i – молярная масса компоненты (кг/моль); R — 8,144 Дж/(К ^ моль) - универсальная газовая постоянная; коэффициент 6 г — 3/2 - для одноатомного газа, 6 г — 5/2 - для двухатомного, 6 г — 6/2 - для трехатомного. AE ^{( j )} -энергетический выход реакции (Дж/моль).

Суммирование в (2) и (5) производится по всем учитываемым химическим реакциям. В уравнении (7) суммирование производится по всем компонентам смеси. Уравнения для скоростей химических реакций g i записываются для каждого конкретного рассматриваемого случая. Так, при рассмотрении реакции окисления окиси углерода мы будем использовать

g ⁽2CO+o 2 ^ 2CO 2 ) — ₇ • iQ ii _{n co} exp( - 96370/RT).

Система уравнений (1) – (8) совместно с уравнениями для скоростей рассматриваемых химических реакций представляет собой математическую модель процесса распространения ударной волны по двухфазной среде (газ – конденсированная фаза) с химически активной газовой фазой.

Метод решения и результаты расчетов

При численном решении системы уравнений (1) – (8) целесообразно использовать метод разделения по физическим процессам. На первом этапе рассматривается химически замороженная смесь, и система уравнений решается методом, подробно представленным в работе [4], а на втором этапе решаются уравнения химической кинетики по неявной схеме.

В проведенном нами численном моделировании рассматривался объем среды с начальным давлением P g — 1 атм и плотностью p g — 1, 29 кг/м ³ , в котором в начальный момент времени на расстоянии 1 м от земли расположена цилиндрическая область повышенного давления P i и плотности p i радиусом 0,1 м. Область повышенного давления создается продуктами взрыва цилиндрического заряда с уравнением состояния (5), начальной плотностью p i — 1052 кг/м ² и теплотой сгорания Q — 5447 кДж/м ³ .

Газовая смесь включала четыре компонента: N 2 , O 2 , CO и CO 2 . Как показано в работах [1, 2], учет этих четырех компонентов позволяет адекватно описывать распространение УВ в лесу при наличии пожара. Проводился учет химической реакции окисления окиси углерода. В области повышенного давления, имитирующей продукты взрыва, брались следующие начальные концентрации компонентов смеси C n ₂ = 0, 78, C q ₂ = 0, 21, C co = 0 и C co ₂ = 0, 01. Начальная концентрация компонентов в области нормального давления (окружающая среда) определялась рассматриваемой задачей. Наличие конденсированной фазы учитывалось через силу межфазного взаимодействия f . При фиксированном диаметре частиц d = 0,1 мм параметром, определяющим характеристики конденсированной фазы, служила объемная концентрация частиц а.

Рассматривались две различные ситуации:

• 1)    распространение ударной волны в химически инертной газовой фазе без конденсированной фазы а = 0 и без учета химических реакций - концентрации веществ в окружающей среде C n ₂ = 0, 78, Co₂ = 0, 21, C co = 0 и C co ₂ = 0, 01 — такие же, как и в области продуктов взрыва;

• 2)    распространение ударной волны в химически активной газовой смеси при наличии конденсированной фазы а = 0, 001, с учетом химических реакций - концентрации веществ в окружающей среде C n ₂ = 0, 725, C o ₂ = 0, 205, C co = 0, 06 и C co ₂ = 0, 01 - содержит окись углерода.

В ходе расчетов контролировалось выполнение закона сохранения энергии. Так, в отсутствии химических превращений полная энергия системы сохранялась в ходе расчетов с точностью не хуже 0,3%. При наличии химических реакций полная энергия системы увеличивалась за счет энерговыделения в ходе реакций. При наличии в системе частиц конденсированной фазы полная энергия газовой фазы уменьшалась, даже при наличии реакций, за счет работы против сил сопротивления.

На рис. 1, 2 приведено поле давления для этих двух случаев в различные моменты времени (0,65 мс и 1,5 мс). Сравнение результатов показывает, что интенсивность УВ увеличивается из-за протекания химической реакции, как при отсутствии частиц конденсированной фазы, так и при их наличии. Аналогичное поведение – усиление УВ при взрыве заряда в горящем лесу – наблюдается и в эксперименте [1]. Однако наличие частиц конденсированной фазы даже в столь малой объемной концентрации (а = 0, 001) оказывает на динамику распространения УВ влияние не меньшее, чем учет химических реакций.

Рис. 1. Поле давления в момент времени t = 0, 65 мс: 1) в инертном газе; 2) в газовой смеси с частицами и с химическими превращениями

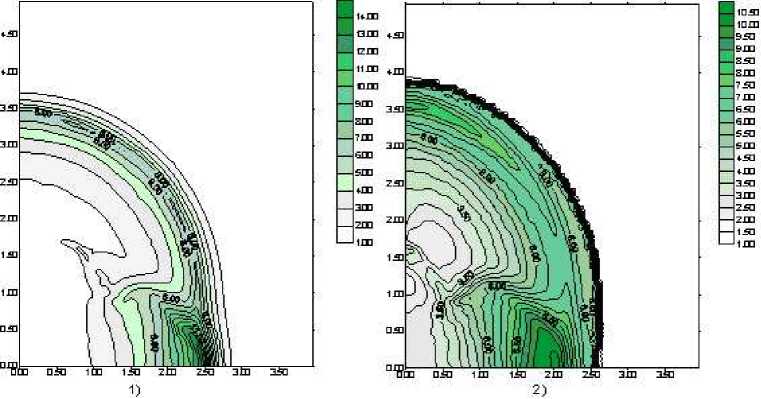
Рис. 2. Поле давления в момент времени t = 1 , 5 мс: 1) в инертном газе; 2) в газовой смеси с частицами и с химическими превращениями

Заключение

В результате проведения сравнительного численного исследования влияния химических реакций и сопротивления со стороны частиц конденсированной фазы на динамику распространения цилиндрически расходящейся ударной волны были получены следующие результаты:

• 1.    Предложена численная схема для описания динамики двухфазной гетерогенной среды с химически активной газовой фазой.

• 2.    Показано, что протекание в газовой смеси химических реакций приводит к повышению энергии системы и интенсивности распространяющейся по смеси УВ, что соответствует экспериментальным результатам [1].