Математическое моделирование распространения звука по дыхательным путям в условиях измененной газовой среды

RUSSIAN JOURNAL OF BIOMECHANICS

Известно, что в результате воздействия измененного состава газовой среды (ГС) меняется функциональное состояние дыхательной системы человека. В некоторых случаях это может приводить к возникновению заболеваний. Данная проблема имеет особенное значение в областях подводной и космической медицины, поскольку люди подвергаются длительно- му воздействию измененной ГС.

Для предупреждения патологических состояний дыхательной системы у космонавтов рекомендуется проводить оценку вентиляционной способности легких. Однако применение традиционных способов, например, спирометрии, в космическом полете имеет ряд сложностей. Вследствие этого предлагается использовать методы респираторной акустики, которые включают в себя регистрацию и анализ трахеальных

0009-0004-7376-1713

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

дыхательных шумов (ДШ) [1]. Для данного анализа требуется понимать механизмы генерации и распространения ДШ.

Цель работы заключалась в разработке математической модели генерации и распространения звуковых колебаний в дыхательных путях человека при дыхании измененной ГС. Ранее в научной литературе рассматривались модели распространения звуковых колебаний по дыхательным путям человека. В работах [2; 3] использованы электромеханические аналогии, в [4; 5] — уравнения акустики. Относительная роль структурного (по тканям стенок дыхательных путей) и воздушного (по газу, находящемуся внутри дыхательных путей) путей распространения звука все еще дискутируется [4; 6-8]. Далее мы принимаем концепцию воздушного пути, то есть волновода с податливыми стенками, как основного пути распространения ДШ от мест генерации в дереве дыхательных путей до трахеи.

Акустические свойства дыхательного тракта и легких важны также для трактовки результатов импульсной осциллометрии системы дыхания. Алгоритмы определения импедансных характеристик легких применяются для анализа результатов воздействия различных факторов на систему дыхания [9; 10].

Методы респираторной акустики могут быть особенно важны и в других условиях, когда традиционные способы исследования дыхания сложно применить, а изменения ДШ значительные. ДШ изменяются при остром состоянии [11; 12]. Изменения ДШ происходят и в условиях изменения состава и давления дыхательной газовой смеси [13; 14]. При этом изменяются физические характеристики дыхательной газовой смеси и параметры, поэтому понимание особенностей генерации и распространения звука в легких представляет собой дополнительную сложность и особый интерес.

Материалы и методы

Расчетная схема модели

Для описания размеров и механических свойств дерева дыхательных путей человека при математическом моделировании движения газов в дыхательных путях используются различные модели [1; 4-6; 15-17]. Как одна из наиболее обоснованных полных моделей всего дерева дыхательных путей человека, нами выбрана асимметричная модель бронхиального дерева, описанная в работах [2; 18-20]. В этой модели самый крупный дыхательный путь (трахея) считается путем поколения 0, далее по мере ветвления номера поколений дочерних бронхов возрастают на 1 или более. Для расчетов бронхиальное дерево разбивалось на малые фрагменты, или сегменты, в пределах которых площадь поперечного сечения считается постоянной.

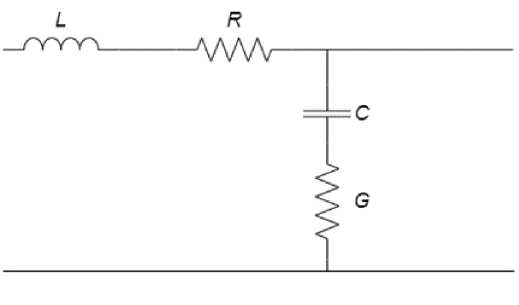
Каждый сегмент был представлен в виде Т-образной эквивалентной схемы отрезка трубы [21]. Такая схема включает в себя следующие параметры: сопротивление R , индуктивность L , емкость C и проводимость G (рис. 1, а ).

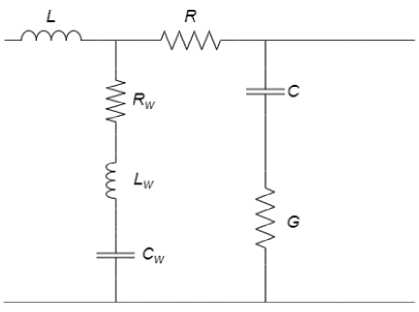
Также, аналогично [15; 18], в расчетную схему включены такие параметры стенок сегмента дыхательных путей, как сопротивление R w , инерционность L w и растяжимость C w . Данные элементы подключаются последовательно относительно друг друга и параллельно емкости C и проводимости G (рис. 1, б ).

Порядок вычислений

Поскольку на текущем этапе моделирования нас интересуют трахеальные дыхательные шумы, то в данной модели не рассматриваются акустические эффекты ротовой полости и гортани. Считается, что внегрудной участок трахеи через открытый рот выходит прямо в окружающее пространство. В дальнейшем планируется оценить, как различается амплитуда звука в трахее в крайних вариантах: как с полностью открытой, так и полностью закрытой трахеей.

На первом этапе производилось вычисление им-педансов Z для потока газа от крупных дыхательных путей к мелким, согласно формуле (1) [22]:

Z t + Z o tanh( у 0 1 )

Г Z. I           ’

¹ + 1 у¹ I tanh( Y о l )

V Z о J

где ZT - импеданс на входе сегмента N дыхательных путей, Z 0 - акустический импеданс сегмента Nx дыхательных путей, Y 0 - постоянная распространения, l - длина сегмента Nx дыхательных путей.

Расчеты проводились для первых 10 поколений дыхательных путей, так как предполагается, что в более мелких дыхательных путях никакие звуки не генерируются, поскольку потоки слишком малы.

Исследования характеристик генерации шумов на симметричной физической модели голосовой щели человека показали, что амплитуда акустических колебаний давления, генерируемых на сужении голосовой щели, пропорциональна второй степени линей-ной/объемной скорости потока воздуха в трахее [ 23]. Фактически аналогичное выражение для мощности шумов, генерируемых в каком-либо участке дыхательного тракта, предложили в [18].

Далее мы принимаем, что в области изменения площади поперечного сечения бронхиального дерева между поколениями N x и N x +1 (рис. 2) генерируется звук в соответствии с уравнением (2) [18]:

P rms

PoVd I _ Ке 2 с     I    Recrit

SПо J

,

а

б

Рис. 1. Т-образная эквивалентная схема сегмента бронхиального дерева: а - исходная схема; б - схема, учитывающая свойства стенок сегмента

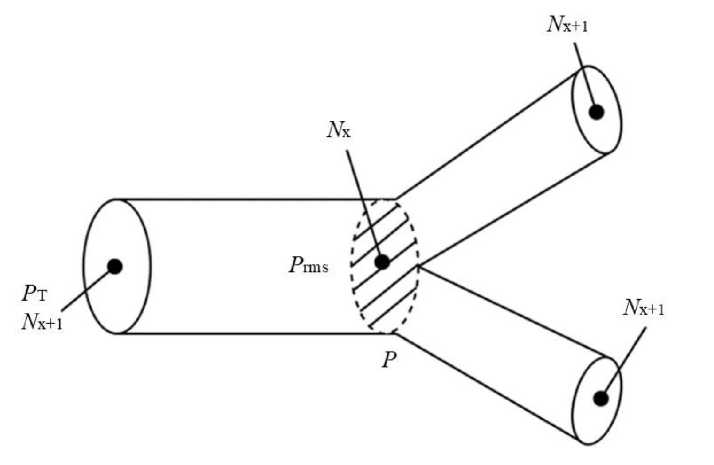
Рис. 2. Схема сегмента с сечениями N x- 1 / N x и N x /N_{x +1}

где Prms - давление мощности звука, K - константа, р0 - плотность воздуха, V - поток, d - диаметр сегмента Nx, S - площадь поперечного сечения сегмента Nx, По - вязкость воздуха, Recrit - критическое число Рейнольдса. Звук генерируется, если скорость потока выше критической. Наличие критической скорости воздушного пока, ниже которой ДШ совсем не генерируются, было также обнаружено в ряде других работ [24].

Поскольку звуки, генерируемые между сечениями N x- 1 /N x и N x / N x ₊₁ , никак не коррелированы, то считается, что давление общего звука есть арифметическая сумма давлений (3):

P t = P + P rms ,                    (3)

где P - давление звука в сегменте N x _-1 .

Моделирование распространения звука проводилось для трех газов при давлении 1 атм.: воздуха, кислородно-гелиевой (КГС) и кислородно- криптоновой (ККрС) смесей. Некоторые физические свойства рассматриваемых газов приведены в таблице.

Результаты их обсуждение

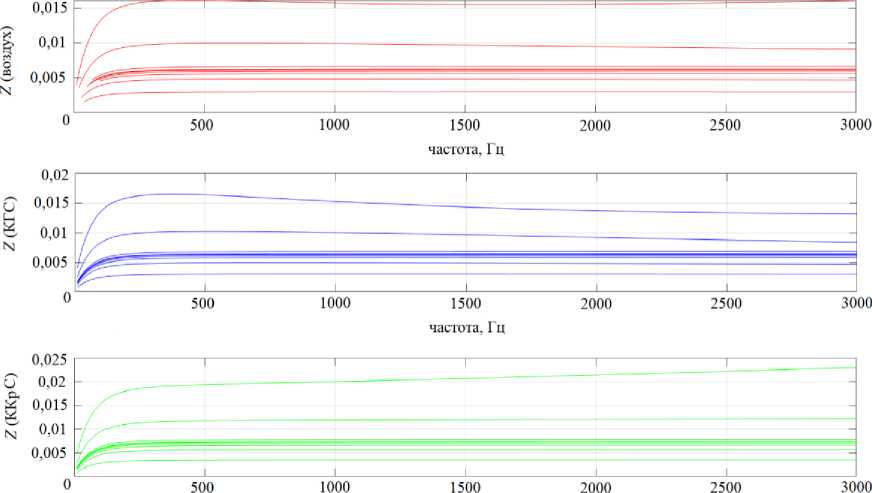
На первом этапе расчетов получена кривая зависимости импеданса от частоты (рис. 3). На графиках представлены кривые, описывающие изменение импеданса для поколений от 0 до 9 дыхательных путей (сверху вниз).

Из графика видно, что при дыхании воздухом импеданс резко возрастает и достигает максимума на частотах 250–300 Гц, затем при дальнейшем увеличе- нии частот остается на уровне около 0,016 (дин/см2)/(см3/с). Для КГС после достижения максимума характерно снижение импеданса, что упоминается в работах [16; 25; 26]. При ККрС, наоборот, величина импеданса увеличивается с возрастанием частоты, что особенно видно в нулевом поколении дыхательных путей.

Свойства дыхательных газов

Состав газа	Плотность газа, г/см3	Динамическая вязкость, (дин · с)/см2
Воздух (21 % О 2 )	1,14 · 10-3	1,86 · 10-4
КГС (20 % О 2 , 80 % Не 2 )	0,46 · 10-3	1,96 · 10-4
ККрС (2 % О 2 , 79 % Kr 2 )	2,74 · 10-3	2,58 · 10-4

частота, Гц

Рис. 3. Зависимость импеданса Z (дин/см²)/(см³/с) от спектра частот

На втором этапе расчетов были получены кривые зависимости звукового давления от величины потока при Re_crit = 1800 (рис. 4) и Re_crit = 2700 (рис. 5).

На рис. 4 и 5 представлены графики звукового давления для нескольких поколений дыхательных путей (от трахеи к последующим более мелким бронхам, сверху вниз). Видно, что величины давления при разных газах значительно отличаются, предположительно, из-за разных свойств рассматриваемых газов.

Кроме того, заметно отличаются начальные величины потока для наименьшего поколения бронхов (особенно видно на графиках для КГС), что также можно объяснить различиями в физических свойствах газов. Расчетные минимальные скорости потока, при которых начинается генерация ДШ, можно сопоставить с экспериментальными данными 3,7 ± 1,7 (мл/с)/кг [24]. Учитывая разные группы испытуемых, для которых были построены морфометрические модели дыхательных путей и измерены минимальные скорости потока, соответствие можно признать удовлетворительным.

Также стоит отметить, что при Recrit = 1800 звук генерируется на два поколения бронхов раньше, чем при Recrit = 2700. Данное явление можно объяснить тем, что во втором случае в меньшем количестве поколений трахеобронхиального дерева число Рейнольдса потока становится больше критического значения, что, в свою очередь, обусловливает появление звука.

Заключение

В данном исследовании была разработана математическая модель генерации и распространения звуковых колебаний в дыхательных путях человека для улучшения качества анализа трахеальных дыхательных шумов. Были получены зависимости импеданса от частот и звукового давления от величины потока; выявлено, что при использовании более плотных газов, чем воздух, импеданс постоянно возрастает. При более легких газах, напротив, импеданс снижается. Данные явления особенно характерны для более крупных бронхов. Также отмечено, что при критическом числе Рейнольдса, характеризующем ламинарное течение, генерация звука происходит на несколько поколений бронхов ранее, чем при переходном режиме течения потока.

Следующим этапом планируется провести валидацию разработанной математической модели в исследованиях с участием испытателей-добровольцев. Сопоставление полученных расчетных зависимостей с экспериментальными данными позволит улучшить и дополнить данную модель, а

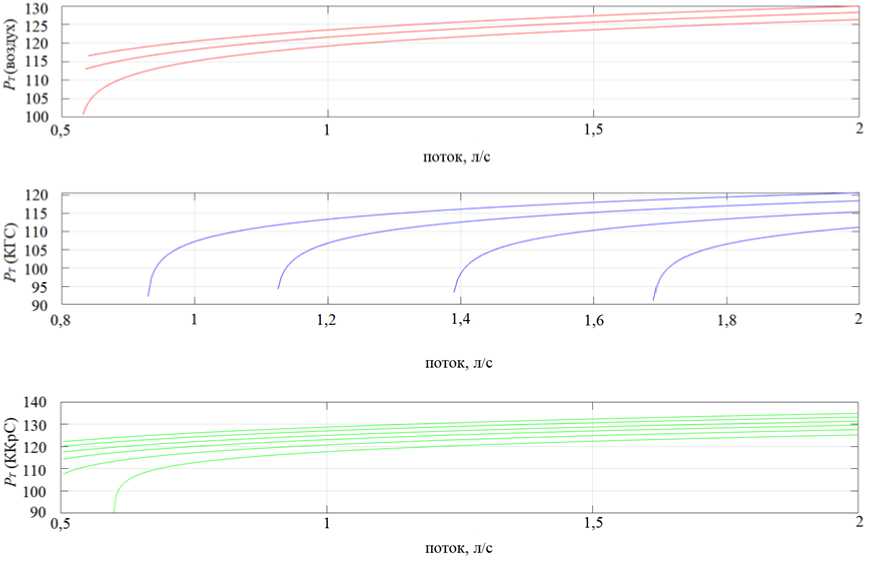
Рис. 4. Зависимость звукового давления P_T (дБ) от величины потока при Re_crit = 1800

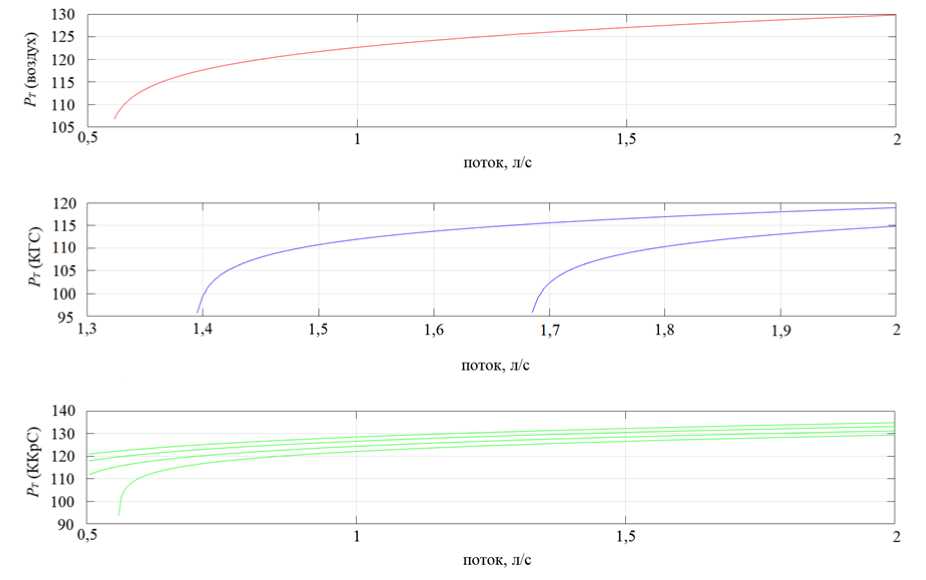
Рис. 5. Зависимость звукового давления P_T (дБ) от величины потока газа при Re_crit = 2700

также получить новые знания о механизмах генерации и распространения звуковых колебаний в дыхатель- ных путях человека с учетом свойств используемых ГС.