Математическое моделирование разветвленных гидравлических сетей

Введение. Водораспределительные сети городов – сложные системы, включающие насосные станции, водонапорные башни, насосы подкачки и трубопроводы, состоящие из множества труб различного диаметра и длины и большого числа потребителей. Возможности современной вычислительной техники позволяют проводить анализ работы сетей любой сложности.

Постановка задачи. Некоторые авторы расчет распределения жидкости в разветвленной сети предлагают проводить по упрощенной динамической модели без учета инерционных сил жидкости и волновых процессов. Такая модель не дает правильной картины переходных процессов, но при отсутствии кавитационных явлений на участках сети обеспечивает достоверный результат в установившемся режиме работы.

Основой программы модели сети являются математические модели всех входящих в нее элементов. Рассмотрим работу одного участка сети (рис.1).

Рис.1. Расчетная схема участка сети ( P ₁₁ , q ₁₁ , z ₁ – давление, расход и геометрическая высота одного конца линии 1 (первый индекс), входящего в узел 1 (второй индекс); P ₁₂ , q ₁₂ , z ₂ – давление, расход и геометрическая высота второго конца линии 1, входящего в узел 2; l ₁ , d ₁ , S ₁ – длина, внешний диаметр, толщина стенки трубы участка 1)

Решение задачи. Условимся считать расход, входящий в линию, положительным, а вытекающий – отрицательным.

Без учета инерционных сил жидкости и волновых процессов работу одного участка можно описать следующими уравнениями:

q 11 = f (P11);(1)

qi2 = ^J - p2 sign(-P12);

у p

P11 + pgz 1 = P12 + pgz 2 + dP1 ;(3)

dP11 = C 1(q 11 + q 12).

dt

Уравнение (1) – это характеристика источника (насоса). Уравнение (2) представляет собой характеристику стока (потребителя), где µ – коэффициент расхода, ω – площадь отверстия, ρ – плотность жидкости, g – ускорение свободного падения.

Уравнение Бернулли (3) записано для узлов 1 и 2, где dP1 – потери давления в линии 1, при этом dP1

l ρ v ^{2 λ} d 2 ,

где l – длина трубы; λ – коэффициент гидравлического трения; d – внутренний диаметр трубопровода; v – средняя скорость жидкости в трубе.

Уравнение (4) связывает производную давления по времени с приведенной жесткостью

С ₁ рассматриваемого участка и балансом расходов по концам линии, при этом

• 4     E _Ж

С1=πd2l1+dнEЖ , SEТР где EТР – модуль упругости материала трубопровода; EЖ – модуль упругости жидкости;

• d _н – наружный диаметр трубопровода; S - толщина стенки трубы.

Таким образом, система уравнений (1)-(4) позволяет определить параметры потока на каждом участке.

Основываясь на этих уравнениях, можно составить математическую модель сети любой сложности. Рассмотрим сеть, состоящую из двух насосов, двух потребителей и четырех линий (рис.2).

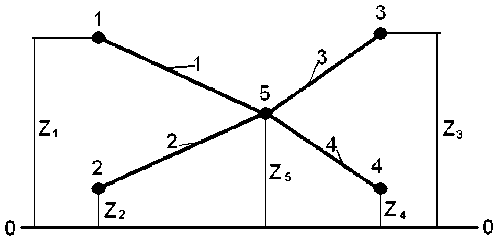
Рис.2. Схема двухнасосной сети

Расходы q ₁₁ на стороне линии 1, присоединенной к узлу 1, и q ₂₂ на стороне линии 2, подсоединенной к узлу 2, определяются характеристикой источников и зависят от давлений в узлах:

q11 = f(P11) ;(5)

q22 = f (P22) .(6)

Расходы q ₃₃ на стороне линии 3, подсоединенной к узлу 3, и q ₄₄ на стороне линии 4, подсоединенной к узлу 4, соответственно:

q33 = µω3    P33 I sign(- P33 ) ;(7)

ρ q44 = µω4 3 H P44 I sign(- P44 ) .(8)

Уравнения Бернулли для линий:
P 11 + p gz 1 = P 15 + p gz 5 + dP ;	(9)
P 22 + p gz 2 = P 25 + p gz 5 + dp , ;	(10)
P 35 + P gz 5 = P 33 + P gz 3 + dP 3 ;	(11)
P 45 + P gZ 5 = P 44 + P gZ 4 + dP 4 .	(12)
Производные давления в линиях:
dP 11 ,   = C 1 ( q 11 + q 15 ) ; dt	(13)
dP 22 — C 2 ( q 22 + q 25 ) ; dt	(14)
,, — C 3 ( q 35 + q 33 ) ; dt	(15)
dP 45 — C 4 ( q 45 + q 44 ) . dt	(16)
Баланс расходов в узле 5:
q 15 + q 25 + q 35 + q 45 — 0 .	(17)

Следствием соединения линий в узле 5 является равенство давлений на сторонах линий, подсоединенных к узлу, давлению в узле 5:

P i5 = P 25 = P 35 = P 45 = P 5 . (18, 19, 20, 21)

Таким образам, мы получили систему из 17 уравнений, которые определяют 17 неизвестных. Четыре уравнения дифференциальные (число линий), остальные алгебраические. Расходы источников ( q ₁₁, q ₂₂ ) и стоков ( q ₃₃ , q ₄₄ ) выражены в явном виде. Получим выражение в явном виде для расходов на сторонах линий, сходящихся в узле 5 ( q ₁₅, q ₂₅, q ₃₅, q ₄₅ ).

Продифференцируем выражения (9)-(11) по времени и, пренебрегая величинами второй степени малости (при решении системы уравнений численным методом изменение расхода на шаге интегрирования есть величина бесконечно малая), имеем:

dPiL —     ;(22)

dt dt dP2L — dP2L ;

dtdt dP = dP».(24)

dtdt

Заменяя в уравнениях (18)-(20) давления на их производные с учетом уравнений (22)-(24) получим три уравнения, связывающие расходы на сторонах линий, сходящихся в узел 5:

С1 (q 11 + q 15 ) — C2 (q22 + q25 ) ;

С2(q22 + q25) — C3(q35 + q33) ;

С3 (q35 + q33 ) — C4 (q45 + q44 ) .(27)

Решая систему алгебраических уравнений (25)-(27), (17) находим в явном виде расходы на сторонах линий в узле 5:

1

1 (

+ q 33

(28)

q 15

1 C 1

1 +--+ C 2

1 C 3

+

1 C 4

C 1

q 11

q 22

q 44

q 11 ;

1

1

+ q 22

+ q 33

+ q 44 ) -

(29)

q 25

1 C 1

1 +--+ C 2

1 C 3

+

1 C 4

C 2

q 11

q 22 ;

1

1 (

+ q 22

+ q 33

+ q 44 )-

(30)

q 35

1 C 1

1 +--+ C 2

1 C 3

+

1 C 4

c C 3

q 11

q 33 ;

q 45 =

1

1

+ q 22

+ q 33

+ q 44 )-

(31)

1 C 1

1 +--+ C 2

1 C 3

+

1 C 4

C 4

q 11

q 44 .

Следовательно, работа сети (рис.2) описывается системой уравнений (5)-(16), (21), (28)-(31), решение которых численным методом позволяет определить все неизвестные.

Можно записать общую формулу определения расходов на стороне n линий, подключенных к k -му узлу:

q j ( k )

ⁿ 1 C j

Z Cj

Z q_jW

q j (...) .

Здесь q _{j ( k )} – расход на стороне j -ой линии, подключенной к k -му узлу; С_j - жесткость j -ой линии; q _{j (...)} - расход на другой стороне j -ой линии.

Заключение. Таким образом, уравнения (1)-(4), (32) являются основой для математической модели водораспределительной сети любой сложности и различной топологии. На основе математической модели составляется программа решения системы уравнений численным методом с использованием подпрограммы Рунге – Кута, которая позволяет анализировать на ЭВМ работу водораспределительных сетей любой сложности, но в связи с принятыми допущениями не позволяет анализировать переходные процессы в сети. Для их анализа необходима уточненная математическая модель, учитывающая инерционные силы жидкости, волновые и кавитационные явления.

Материал поступил в редакцию 11.11.10.

V.S. KRUTIKOV, K.A. LIKHODED, N.V. DIVULIN

MATHEMATICAL MODEL OF SUBDIVIDED HYDRAULIC CIRCUITS

The mathematical model of subdivided hydraulic circuits that permits calculation of the fluid distribution in all points is considered.

КРУТИКОВ Валерий Сергеевич (р. 1941), доцент кафедры «Гидропневмоавтоматика и гидропривод» Южно-Российского государственного технического университета, кандидат технических наук (1970), доцент (1981). Окончил Новочеркасский политехнический институт (1963). Область научных интересов: гидравлические машины, аппараты и гидропривод.

Автор 54 публикаций.

ЛИХОДЕД Константин Анатольевич (р. 1976), старший преподаватель кафедры «Гидропневмоавтоматика и гидропривод» Южно-Российского государственного технического университета. Окончил Новочеркасский политехнический институт (1997).

Область научных интересов: гидравлические машины, аппараты и гидропривод.

Автор 20 публикаций.

ДИВУЛИН Николай Васильевич (р. 1977), старший преподаватель кафедры «Гидропневмоавтоматика и гидропривод» Южно-Российского государственного технического университета. Окончил Новочеркасский политехнический институт (1999).

Область научных интересов: гидравлические машины, аппараты и гидропривод.

Автор 12 публикаций

Valery S. KRUTIKOV (1941), Associate Professor of the Hydropneumoautomation and Hydrodrive Department, South-Russian State Technical University. Candidate of Science in Engineering (1970), associate professor (1981). He graduated from Novocherkassk Polytechnic Institute (1963).

Research interests: hydraulic machines, apparatus and hydrodrive.

Author of 54 publications.

Konstantin A. LIKHODED (1976), Senior Lecturer of the Hydropneumoautomation and Hydrodrive Department, South-Russian State Technical University. He graduated from Novocherkassk Polytechnic Institute (1997).

Research interests: hydraulic machines, apparatus and hydrodrive.

Author of 20 publications.

Nikolay V. DIVULIN (1977), Senior Lecturer of the Hydropneumoautomation and Hydrodrive Department, South-Russian State Technical University. He graduated from Novocherkassk Polytechnic Institute (1997).

Research interests: hydraulic machines, apparatus and hydrodrive.

Author of 12 publications.