Математическое моделирование рефракционных характеристик электромагнитного излучения в стохастическом поле тяготения

DOI:

Как известно [2; 4; 9; 12; 16], электромагнитное излучение удаленных космических источников в процессе распространения к наблюдателю подвержено влиянию окружающих полей тяготения. В частности, транспорт излучения в окрестности массивных астрофизических объектов может сопровождаться рядом значимых эффектов, таких как гравитационное линзирование, фокусировка потока излучения, изменение наблюдаемого спектра и др. [1; 3; 8; 14]. Измеренные характеристики и структурные особенности космического излучения, прошедшего поля тяготения, содержат уникальную информацию о природе скрытых массивных объектов, невидимых в электромагнитном диапазоне, но проявляющих себя через гравитационное взаимодействие. Для более точного восстановления возмущающих гравитационных потенциалов скрытых объектов следует принимать во внимание не только воздействие окружающей случайно-неоднородной плазмы [6], но и гравитационный шум (присутствие хаотических неоднородностей полей тяготения), поскольку последний также может приводить к частичному замыванию и маскировке гравитационных эффектов детерминированных массивных объектов. Следует заметить, что окружающая космическая плазма главным образом оказывает воздействие на распространение электромагнитного излучения радиодиапазона. На излучение более высокочастотного диапазона, когда плазма становится прозрачной, основное влияние оказывают хаотические гравитационные неоднородности.

Согласно общей теории относительности (ОТО), задача распространения электромагнитного излучения в искривленном римановом пространстве, связанном с гравитационным объектом, может быть приближенно сведена к задаче распространения излучения в евклидовом пространстве с эффективным показателем преломления вакуума [15]. Полагая, что показатель преломления такой «вакуумной» среды медленно изменяется на длине волны излучения, расчеты рефракционных характеристик электромагнитных волн будем проводить, используя математический аппарат геометрической оптики [5–7; 10; 11].

Целью работы является исследование методом численно-аналитического моделирования влияния гравитационного шума на распространение высокочастотного электромагнитного излучения в поле тяготения группы астрофизических объектов.

1.    Метод численно-аналитического моделирования

Для учета хаотических гравитационных неоднородностей в поле тяготения группы астрофизических объектов эффективный показатель преломления вакуума представлялся в виде:

П = П о + П 1 ,

где п ₀ связан с регулярной составляющей поля тяготения; П 1 описывает случайные неоднородности показателя преломления, вызванные гравитационным шумом. В рамках ОТО, исключая сильные гравитационные поля, вызванные черными дырами и/или нейтронными звездами, для показателя преломления п ₀ используем приближение [1; 12; 15]:

^П о = 1 -

2Ф( ^ ) с ²

где с — скорость света; Ф( R ) — потенциал уравнения Пуассона и имеет вид:

тяготения, который является решением

Ф

$ ⁾= ^-аШ

а ( — Г ) |^ -V|

d3r,

где G — гравитационная постоянная; о ( — Г ) — плотность распределения массы. В случае ^(7^) = const имеем:

Ф(Я) =

GM

где M — масса объекта.

Подставляя (4) в (2), для регулярного эффективного показателя преломления ва- куума п0 получаем:

^п о — 1 +

2 GM Rc ²

— 1 + ^, ⁺ R ’

где R _g — гравитационный радиус астрофизического объекта.

Задавая более сложные модели o( ^V ), с помощью интегрирования (3) в определенных случаях можно получить функциональные зависимости для эффективного показателя преломления вакуума вблизи группы астрофизических объектов. В настоящей работе предполагается, что каждый астрофизический объект вносит аддитивно свой вклад в общий эффективный показатель преломления вакуума, и используется приближенная модель [5; 6; 11]:

R g

^П " ^—1+ R

N

⁺ ^ ^A i ^{exp[ — b} Ri ^{( R} — ^R Li )^{2 — b} ф i ^{( ф} — ^ф Li^{)2 — Ь}Ы ⁽ 5 — S bj ) ² ], i=1

где N — количество дополнительных астрофизических объектов, формирующих сложную структуру поля тяготения; A _i ,R _Li , ф _Li , 5 _Li , b Ri , b^, b_{5 i} — соответственно доля вклада в общий показатель преломления, координаты точек локализации и пространственные масштабы i -го объекта.

Расчеты рефракционных характеристик электромагнитного излучения при распространении в поле тяготения группы астрофизических объектов выполнялись с помощью системы стохастических лучевых дифференциальных уравнений в форме Эйлера в сферической системе координат [10]:

de dф

dR dф

R ctg в;

.         >       2    , 1 ddⁿ               dn.      .

— (1+tg ² asin ² в)( ( ctg в — R ) — 1); n дф       dR

̃︀

tg a:

da.

dф

1/, . , 2 Qn.,dn - (1 + ctg ² в cos ² a)( — n d 5

-

dn it tg a), d ф

где R(ф), 5(ф), ф — соответственно радиальная и угловые координаты луча; а(ф), в(ф) — углы рефракции луча. Начало системы координат совмещено с центром основного гравитирующего объекта. Источник электромагнитного излучения имеет координаты (Rn; 5n; фп), характеризуется угловыми прицельными параметрами в секторах [an0; anJ и [вп0; вПр]. На расстоянии Rk формируется картинная плоскость наблюдателя, где отмечаются конечные угловые координаты луча 5k, фк• Следовательно, образуется распределение точек, координаты которых находятся в диапазонах [5к0; 5kJ и [фк0; фкр]. Моделируя распределение точек прихода лучей в картинной плоскости наблюдателя, можно приближенно оценить ослабление электромагнитного излучения космического источника. Полагая, что мощность излученного источником поля 170 — 1 cuef, где cuef — условная единица измерения, значение полной мощности в окрестности пункта приема будет равно сумме порций U — ^U0/p cuef, где p — количество лучей. Появление областей сгущения точек прихода лучей в картинной плоскости наблюдателя указывает на линзирование и фокусировку излучения. При описании сложных гравитационных полей для дополнительных астрофизических объектов задаются координаты положения в пространстве (Rl; 5l; фЬ). Геометрию задачи на плоскости можно представить следующим образом (рис. 1).

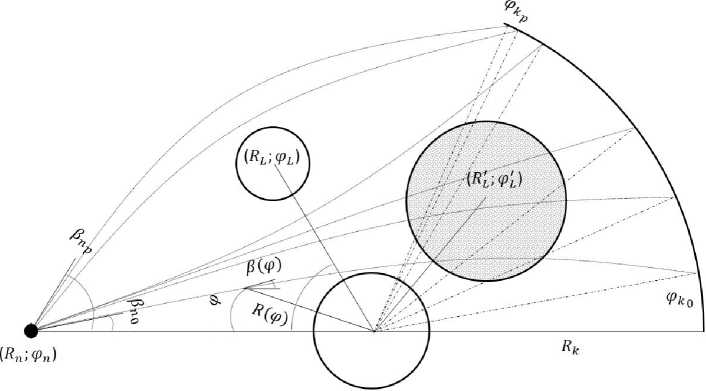
Рис. 1. Геометрия задачи. Вид сбоку. ( R _n ; ф _п ) — положение источника электромагнитного излучения относительно центра основного гравитирующего объекта; (R _l ; ф _Ь ) — координаты дополнительного гравитационного объекта; (R' _l ; ф Ь ) — координаты центра области гравитационного шума; [ в _п0 ; в _п р ] — диапазон угловых прицельных параметров; R _k — расстояние, где формируется картинная плоскость наблюдателя; [ ф ^ ₀ ; ф ^ _р ] — диапазон конечных значений угловых координат лучей, дошедших до картинной плоскости

Для расчета влияния случайного гравитационного шума на распространение электромагнитного излучения уравнения (7) были решены методом возмущений при условии п 1 <<  1. Используя разложения R = R + R 1 ; 5 = 5 ₀ + 5 1 ; в = в о + в 1 ; а = а + а 1 , из системы (7) получена система для флуктуаций траекторных характеристик излучения. Для расчетов боковых отклонений лучей в картинной плоскости наблюдателя использовались уравнения на флуктуации δ 1 и α ̃︀ 1 :

~ d5 1

(1ф

α 1

;

cos ² а о

= (1 + ctg ² в о cos ² а о )( аф                        U 5 о

-

^дп 1 ь

Дф^tg “ ° )'

Система (8) была сведена к дифференциальному уравнению второго порядка:

d 2 5 1 аф ²

= ^{Р (} Ф ⁾⁽дф - ^tg“ 0 ^{) = Т (}”’

где Р (ф) = —¹--+ ctg ² в о .

cos ² а о

Интегрируя уравнение (9) до расстояния R _k и возводя решение в квадрат, после его усреднения по ансамблю хаотических гравитационных неоднородностей имеем дисперсию боковых отклонений луча в картинной плоскости наблюдателя:

" 2 = (1 ^Ф /^{ф Н} ( Ф^Н ( ф^фсф) ’

где Н (ф ' ) = Т (ф ' )(ф — ф ' ); ( ... ) — знак усреднения.

Далее для простоты предполагалось, что гравитационный шум характеризуется гауссовой корреляционной функцией:

*= Y^ o exp[ — (^(^/ — (^УФ^) 2 — ( Ф^ )² ] ,  (11)

где ^ о , v _R , v₅, v_ф — соответственно интенсивность и пространственные радиусы корреляции гравитационного шума, а функция γ описывает его пространственную локализацию. Подставляя функцию корреляции (11) в уравнение (10) и проводя аналитические преобразования, получим выражение:

σ

2 δ

= Г Г фр ( ф - ) р (Ф)(ф — 00

ф ’И ф ^{— ф} '' ^{)( у} 1 + ^ 2 + ^у 3 ^{) С ф} ' ^d^',

2 4(5 ’ — 5 ’’ ) ²          8(5 ’ — 5 '' )(ф ' — ф '' )                  2     4(ф ' — ф ’’ ) ²

где У 1 =       ---; У 2 =                    tg а о ; У з = — —          ’   tg ² а о .

ν_δ ²        ν_δ ⁴                     ν_δ ² ν ² _φ                       ν ² _φ         ν ⁴ _φ

Используя метод суммарно-разностных переменных, где ф ₀ = (ф ‘ + Ф ‘‘ )/2; ^ = ф ‘ — ф ’’ , с дальнейшими аналитическими преобразованиями, из уравнения (12) получаем систему для расчета дисперсии боковых отклонений σ_δ ² лучей, пришедших на картинную плоскость наблюдателя [6]:

^d"2  ПФ П~t^DP 2         ^К м т тп