Математическое моделирование реологического поведения нелинейно-вязких жидкостей, которые демонстрируют проявление эффекта “отвердевания”

Известно достаточно много реологических моделей вязких жидкостей [1-4]. Как правило, все эти модели для случаев одномерного течения различаются лишь степенью нелинейности связи между касательным напряжением т и скоростью сдвига у .

Однако целый ряд результатов, полученных разными авторами в последнее время и приведенных, например, в [5 - 10], а также ряде других работ, указывают на то, что некоторые суспензии на основе мелкодисперсных частиц обладают аномальными реологическими свойствами.

Суть таких особенностей реологического поведения заключается в следующем. При определенной концентрации и размерах мелкодисперсных частиц кривая течения, построенная в координатах “скорость сдвига – касательное напряжение”, демонстрирует резкое возрастание своей кривизны при приближении модуля скорости сдвига к некоторому крити -ческому (но конечному) значению у crit • При этом дилатантное поведение жидкости усиливается настолько, что наиболее деформируемые области течения (где скорость сдвига непосредственно приближается к своему критическому значению) начинают вести себя практически подобно твердому телу. Здесь же заметим, что зам еряемые значения касательно го напряжения в окрестности предполагаемого © Колодежнов В.Н., 2012

критического значения y crit принимают конечные значения, которые, как правило, меньше значений т , получаемых при существенно более низких уровнях скорости сдвига.

Крутизна кривой течения, определяемая в одномерном случае соотношением

_ d |^{т (}| y\ )| ^Ц1 oc =   d v\ ,

характеризует фактически динамическую вязкость жидкости. В частном случае классической ньютоновской жидкости крутизна кривой течения является постоянной величиной, в точности совпадающей с динамической вязкостью. В этом смысле условие

lim

d т

| Г| ^ У crit [ d ^Y

= от

может быть принято в качестве критерия проявления эффекта “отвердевания”.

Характеризуя проявление эффекта “отвердевания”, заметим, что речь здесь не идет об “отвердевании” в смысле фазового перехода типа кристаллизации. При удалении модуля скорости сдвига от своего критического значения вязкость снижается и сплошная среда вновь приобретает свойство “текучести”.

Реологическая модель, демонстрирующая проявление эффекта “отвердевания” в случае монотонного возрастания вязкости. Наиболее простой моделью в рамках обсуждаемого эффекта может быть принята следующая модель с монотонно возрастающей для одномерных случаев крутизной кривой течения

T ij = — P ■ S ij + 2 ■ ц ( 1 2 ) ■ S ij ; i , j = 1,2,3 ;

I2 = 8n ■ 822 + 822 ■ 833 + 833 ■ 8n — 8n — 823 — 831 ;

Ц (12) = T /

■

1 —

2, crit

—

; (2)

2, crit

0 <  n <  1;       |I 2 1 <  1 2, crit ,

где T ij , 8 ij - компоненты тензоров напряжений и скоростей деформаций; P - давление; S ij -символ Кронекера; ц ( 1 2 ) - функция второго инварианта 1 2 тензора скоростей деформаций; T crit - эмпирическая константа, которая для одномерного течения представляет собой касательное напряжение, достигаемое при | у | = у crit ; n - эмпирическая константа; 1 2 crit - критическое значение модуля второго инварианта тензора скоростей деформаций, которое для одномерного сдвигового течения удовлетворяет условию

У crit = ² ■ д/ I 2, crit •

Естественно, что параметр 1 2, crit должен рассматриваться как самостоятельная реологическая константа, определяемая для каждой конкретной жидкости на основе обработки соответствующих экспериментальных данных.

Для предложенной модели на интервале изменения модуля скорости сдвига от 0 до у crit крутизна кривой течения монотонно возрастает. При этом на левом конце интервала для | у | ^ 0 крутизна кривой течения принимает некоторое конечное значение

На правом же конце при | у | ^ у crit крутизна кривой течения, удовлетворяя условию (1), асимптотически стремится к бесконечности.

Отметим, что без изменения сути могут быть предложены и другие формы соотношения (2). Один из таких модифицированных вариантов реологической модели рассматривается в [11, 12].

Реологическая модель, демонстрирующая проявление эффекта “отвердевания” в случае немонотонного изменения вязкости. Целый ряд экспериментальных данных указывает на то, что для одномерных течений таких жидкостей зависимость вязкости от скорости сдвига у не является монотонной и на этой зависимости можно выделить два участка [13, 14].

На первом участке вязкость снижается до некоторого минимального значения, а на втором - возрастает. При этом, как уже отмечалось выше, приближение скорости сдвига к некоторому максимальному по модулю значению приводит к резкому увеличению крутизны кривой течения, что может быть интерпретировано как проявление эффекта “отвердевания”.

Наличие двух участков для области изменения скорости сдвига с, вообще говоря, принципиально различным характером зависимости вязкости жидкости от скорости сдвига предполагает возможность описывать эту зависимость двумя различными функциями. При этом необходимо обеспечить в некоторой точке 1 2, = 1 2, crit 1 “сшивание” не только для этих функций, но и их производных.

С учетом сказанного описание реологического поведения жидкостей такого рода предлагается проводить в соответствии со следующей реологической моделью

T ij =— P ■ S ij + 2 ■ д ( 1 2 ) ■ 8 ij ; i , j = 1,2,3 ;

.lim { R oc ⁽| у\ ^{) }} =

| Y ^ 0

n ■ ^T crit

У crit

^ 1 ^{( 1} 2 ^);                I I 2 I <  ¹ 2, crit 1 ^;

ц ( 1 2 ) = 1                         I I                          (3.

_ ^ 2 ⁽ I 2 ^); I 2, crit 1 < | I 2 I <  I 2, crit 2 ^;

Ц 1 ( 1 2 ) = K 1 ■ (2 ■ дД) n ^{1 —} 1 ;                      (4)

М 2 ( I 2 )

X

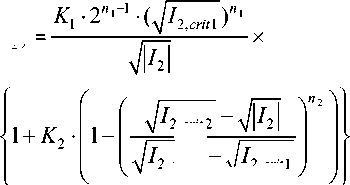
2, crit 2

;    (5)

2, crit 2

2, crit 1

^T crit 2

K I • (2 •д/ Х ^) n ¹

• ⁿ 1 ■ K 1 ■ ^{2 1} ■ ⁽д/ ⁷ 2, crit 2 д/ ⁷ 2, crit 1)

рому критическому, но конечному значению I2,crit2 . Иначе говоря, lim

|⁷ 2| ^ ⁷ 2, crit 2

d т d Y

= от.

Последний результат и позволяет интерпретировать поведение рассматриваемой жидкости с точки зрения проявления эффекта “отвердевания”. Несмотря на неограниченное возрастание крутизны кривой течения при 1 1 2 1 ^ 1 2, crit 2 , касательное напряжение т принимает в этом случае по модулю некоторое предельное и конечное значение T crit 2 .

Здесь же заметим, что согласно приведенной выше модели (3) с учетом (4), (5) минимум вязкости достигается на втором участке в некоторой промежуточной точке, принадлежащей отрезку [ / 2, crit 1 ; ⁷ 2, crit 2 J .

Предложенные выше математические модели носят обобщенный характер и могут быть использованы при описании механического поведения жидкостей, демонстрирующих проявление эффекта “отвердевания” в самых различных системах.

Работа выполнена при поддержке гранта РФФИ, проект № 12-08-00629а.