Математическое моделирование роста эпителиальной ткани
Автор: Красняков И.В., Брацун Д.А., Писмен Л.М.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 4 (90) т.24, 2020 года.
Бесплатный доступ
Развитие компьютерных технологий и быстродействующих вычислительных систем привело к тому, что возникли условия для реалистичного имитационного моделирования биомеханики клеточной ткани, в рамках которой воспроизводится как усредненная сплошносредная динамика ткани, так и поведение каждой отдельной клетки. В данной работе предлагается математическая модель ткани эпителия, которая рассматривается как двумерная. При этом поверхность базальной мембраны, на которой лежит эпителий, в общем случае может иметь сложную двумерную топологию. Модель является дискретной, так как ткань разбивается на клетки, каждая из которых эволюционирует по своему собственному сценарию. Клетка задается многоугольником, число вершин которого и форма могут меняться в ходе эволюции. Модель включает в себя два важных процесса, которые имитируют свойства реальных клеток. Одним из них является митотическое деление клеток, алгоритм которого прописан таким образом, чтобы новая клетка наследовала все свойства старой. Другим важным процессом является интеркаляция клеток, которая делает эпителий подвижной упруго-эластичной средой, адаптирующейся под действием внутренних и внешних воздействий. Для каждой вершины клетки-многоугольника записывается уравнение движения, основанное на эластичной потенциальной энергии. Так как клетка сопротивляется отклонению от среднего объема и чрезмерной деформации формы, то эпителий в целом стремится занять положение, отвечающее минимуму потенциальной энегрии. Хотя клеточная ткань допускает внутреннее движение элементов, она, вообще говоря, является сильно диссипативной средой. Таким образом, биомеханика ткани подчиняется Аристотелевой динамике. Модель допускает простое обобщение на случай обратной связи между биомеханическими и химическими свойствами среды (например, процессы генной регуляции в клетках, приводящие к хемоэластичности), введения нескольких конкурирующих типов ткани (например, возникновение раковой опухоли), трехмерной клеточной ткани. Приводятся конкретные примеры моделирования динамического поведения ткани эпителия.
Имитационное моделирование клеточной ткани, дискретная модель с индивидуальной динамикой, эпителиальная ткань, эластичная потенциальная энергия, хемомеханическое взаимодействие
Короткий адрес: https://sciup.org/146282183
IDR: 146282183 | УДК: 519.876.5 | DOI: 10.15593/RZhBiomeh/2020.4.03
Текст научной статьи Математическое моделирование роста эпителиальной ткани
Человеческий организм состоит примерно из 30 триллионов клеток, которых насчитывается больше 200 видов. Характерный размер клетки очень сильно зависит от её типа. Если исключить весьма специальные клетки (нейроны и яйцеклетки), то можно заметить, что диаметр большинства эукариотических клеток лежит в пределах 5–50 µм. Так, характерный размер человека (1 м) относится к размеру планеты (10 7 м) примерно в той же пропорции, как размер среднестатистической клетки относится к размеру человеческого тела. Таким образом, любой организм биосферы представляет собой сложную систему из огромного множества взаимодействующих между собой элементов. При этом процессы, которые протекают на уровне ядер клеток (например, генная регуляция), не менее важны, чем процессы биомеханики в рамках органа или организма [1]. Это означает, что любое математическое моделирование клеточной ткани, претендующей на реалистичность, должно быть многоуровневым и включать в себя не только усредненную динамику ткани, рассматриваемой как сплошная среда, но и поведение отдельных клеток этой ткани, а также учитывать обратные связи механических явлений с процессами в ядрах клеток.
Математическое и компьютерное моделирование роста ткани используется в различных биологических, биомедицинских задачах, которые включают в себя заживление ран и регенерацию [24], морфогенез [14], возникновение и развитие опухоли [9], синтетическую биологию [8] и др. Рост клеточной ткани может моделироваться в рамках приближения сплошной среды и описываться дифференциальными уравнениями в частных производных, которые включают в себя уравнения реакции–диффузии для концентрации веществ в ткани, уравнения Навье– Стокса или Дарси для скорости элементов среды (в случае наличия текучести) и уравнения упругости для распределения механических напряжений (если среда твердая, но деформируемая). К настоящему моменту имеется достаточно большой список литературы, посвящённый моделям сплошной среды [2, 5, 7, 11], так как методологическая основа этих моделей хорошо разработана, а для решения может быть использован аппарат теории сплошных сред.
Другой подход в моделировании принципиально строится с уровня отдельных элементов большой сложной системы. В рамках этого подхода клетки рассматриваются как отдельные динамические объекты со своей эволюцией. Ранние попытки такого моделирования связаны с клеточными автоматами [30], которые в наиболее простом варианте представляли собой фиксированные в пространстве элементы среды с заданными правилами взаимодействия с соседями. Это позволило получить новые результаты, невидимые в рамках сплошносредного описания [13, 23, 26], но реализация численного расчета в рамках таких моделей оказалась достаточно нетривиальным делом. Кроме большого числа степеней свободы в таких системах, дополнительной сложностью является достижение структурной устойчивости модели в ходе расчета. В настоящий момент, кроме собственно классических клеточных автоматов, существуют различные решётчатые и нерешётчатые модели. Наиболее свежие подходы в моделировании включают в себя индивидуальную динамику клеток на основе сферических частиц или деформируемых элементов.
Модели сферических частиц берут начало из молекулярной динамики [15, 19]. Каждая клетка в такой модели представлена в виде сферы, которая может взаимодействовать с соседними клетками. Сила, действующая между ними, зависит от дистанции между центрами сфер. В модель могут быть включены дополнительные случайные и/или диссипативные силы. Движение частиц определяется вторым законом Ньютона. В рамках модели клетки могут делиться, умирать и изменять свой тип. Разные типы клеток могут иметь разные характеристики с точки зрения их движения, деления и смерти. Например, в работе [15] были исследованы одноклеточные слоистые ткани, где предполагалось, что между клетками действуют дополнительные силы адгезии. Существуют модели, где клетки рассматриваются как многоугольники с центрами, связанными упругим элементом, а форма клетки определена как многогранники Вороного в моделях клетка–центр. Это подход был использован, например, для моделирования железистой полости [28]. Часть таких моделей может комбинироваться с моделями сплошной среды [22] и уравнениями переноса для внутриклеточных и внеклеточных концентраций различных веществ.
Наиболее современные модели деформируемой клетки принимают во внимание геометрию клетки и возможность её деформации, обусловленную как внешними, так и внутренними силами. Если под внешними чаще всего понимают силы механической природы (давление клеточной ткани), то внутренняя сила вполне может быть активной силой, появляющейся в результате команды, поступившей из ядра клетки. Дискуссия об активных силах в биологии до сих пор продолжается [24], так как их появление на физическом уровне описания выглядит странным. Однако, по-видимому, на основе чисто механических сил полностью объяснить процессы в клеточных тканях (например, морфогенез) не представляется возможным. Возвращаясь к методу, отметим, что мембрана клетки в рамках этого подхода может считаться как ансамбль частиц с различными силами, действующими на них. Этот метод предоставляет более детальную информацию о геометрии клеток, адгезии и деформациях, но он сложнее в численной реализации, особенно в случае деления клеток. Если алгоритмы деления прописаны недостаточно вдумчиво, модель не будет работать из-за геометрических ограничений или постепенного накопления механических напряжений в клеточной среде. Существуют различные реализации модели деформируемых клеток. Вопрос о геометрической поляризации клеток в ткани рассматривался в [29]. Задача о заживлении раны была рассмотрена в [24]. Явление миграции клеток при развитии опухоли рассматривалось в работах [18, 27]. В работах [3, 9] авторами было изучено структурообразование при росте карциномы при помощи модели деформируемой клетки. Рост ткани в условиях сильно деформируемой базальной мембраны эпителия изучался в работе [31]. В этих работах при численной реализации использовались модели с тысячами и десятками тысяч клеток.
В данной работе обсуждается методология построения многоуровневой модели двумерной клеточной ткани, которая включают в себя деформируемые клетки с индивидуальной динамикой. Приводится несколько конкретных примеров численного расчета. Обсуждается стратегия моделирования различных процессов в ткани.
Свойства эпителиальной ткани
В данной работе мы фокусируемся на построении модели эпителиальной ткани, которая играет в организме очень важную роль, формируя внешний контур внутренних органов, а также защищая весь организм от внешней среды. Важной особенностью эпителия, удобной для моделирования, является его квазидвумерность.
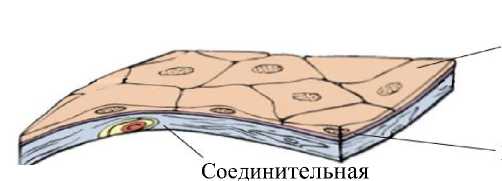
Эпителиальная ткань – это совокупность полярных дифференцированных клеток, тесно прилегающих друг к другу в виде пласта, лежащего на базальной мембране (рис. 1). Эпителий лежит на границе внешней или внутренней среды организма и образует большую часть желёз. Например, эпителий выстилает поверхность кожи, роговицы глаза, серозных оболочек, внутреннюю поверхность полых органов пищеварительной, дыхательной и мочеполовой систем, а также образует желёзы. В эпителии отсутствуют межклеточное вещество и кровеносные сосуды, однако имеется обильная иннервация. Клетки эпителия в совокупности образуют сплошной пласт, расположенный на базальной мембране, через которую ISSN 2409-6601. Российский журнал биомеханики. 2020. Т. 24, № 4: 439–454 441
Эпителий
Базальная мембрана ткань
Рис. 1. Схематическое изображение простой плоской однослойной ткани эпителия осуществляется питание эпителиальной ткани. Клетки плотно примыкают друг к другу при помощи десмосом – особых множественных структур субмикроскопических размеров, которые располагаются на смежных поверхностях соседних клеток. Эпителий обладает высокой регенераторной способностью, и целостность поврежденного пласта, как правило, быстро восстанавливается [24].
Существует несколько классификаций эпителиальных тканей, однако наиболее распространена морфологическая классификация, в которой эпителий разделяют по числу слоёв (одно- или многослойный) и форме клеток (плоская, кубическая, призматическая). По форме клеток эпителий подразделяется на цилиндрический, кубический и плоский, а по расположению клеток – на однослойный и многослойный. В однослойном эпителии все клетки лежат на базальной мембране (см. рис. 1). Если при этом клетки имеют одинаковую форму, т. е. изоморфны, то их ядра расположены в один ряд – это однорядный эпителий. С определенными оговорками такую клеточную ткань можно считать двумерной, что существенно упрощает математическую модель и численные расчеты.
Дискретная модель эпителия с индивидуальной динамикой клеток
Опишем основные особенности предлагаемой модели. Она включает в себя динамику отдельных клеток, представленных формально в виде многоугольников. Число сторон многоугольника является индивидуальной особенностью каждой клетки и может динамически меняться в ходе её эволюции. Как известно, существует только три типа паркета (под паркетом понимается плоскость сплошного заполнения), которые
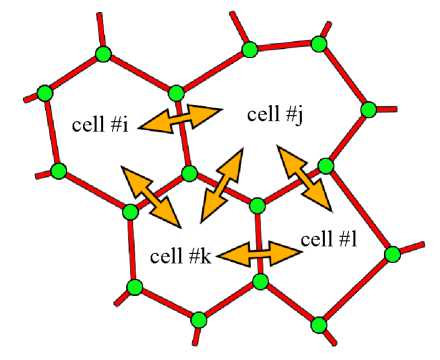
Рис. 2. Схематическое изображение модели эпителиальной ткани с клетками, задаваемыми многоугольниками и обменивающимися химическими сигналами.
Зелёными точками отмечены вершины, на которые действуют силы можно составить из правильных многоугольников – треугольный, квадратный и гексагональный [12]. Наиболее естественным в данном случае выглядит паркет, составленный из правильных гексагонов. Эта форма заполнения плоскости весьма популярна в природе (пчелинные соты, конвективные ячейки Рэлея–Бенара, форма молекулы графена и т.д.). Кроме этого, гексагон является энергетически весьма выгодной формой для клетки, так как такая форма наиболее близка к окружности. Таким образом, в качестве начального условия для ткани задаётся либо гексагональный паркет, либо плоскость, которая состоит из случайных многоугольников. В целом система клеток откалибрована таким образом, чтобы наиболее вероятной формой в ходе эволюции была бы гексагональная форма, но появление других видов многоугольников не исключено. Клетки плотно примыкают друг к другу, образуя сплошную поверхность без просветов, как и в естественном эпителии (рис. 2). Перечислим минимальный набор свойств, которыми должна обладать разрабатываемая математическая модель:
-
• динамическое изменение размера и формы клетки в процессе эволюции ткани под действием изменений локальных механических свойств среды;
-
• пролиферация ткани эпителия посредством деления клеток в определённых условиях эволюции, которые обсуждаются ниже;
-
• смещение или перемещение (в определенных задачах) клеток в общей массе эпителия посредством механизма интеркаляции для снятия локальных напряжений в ткани эпителия;
-
• обмен химическими сигналами, осуществляемый между соседними клетками эпителия через общую границу (см. рис. 2);
-
• конструирование обратных связей между химическими сигналами и биомеханическими свойствами ткани.
Как известно, для поддержания жизни клетки, ей необходимо потреблять питательные вещества, которые поступают из базальной мембраны и ближайшего кровеносного сосуда. Получив необходимое количество вещества, клетка распределяет его остатки между соседними клетками. Хотя процесс переноса веществ в клетках весьма сложный, проще всего смоделировать его с помощью межклеточной диффузии, уравнение которой для каждой клетки можно записать следующим образом:
dC
— = Ф( C)-вс C +Х J, dt adj где C – концентрация питательного вещества; βC – коэффициент деградации, который можно интерпретировать как скорость потребления питательного вещества клетками эпителия. В общем случае (1) является системой уравнений и должно быть написано для каждой клетки. Поле концентраций C не является непрерывным, так как каждая клетка является пикселем поля. Будем полагать, что внутри одной клетки концентрация вещества релаксирует настолько быстро, что в любой момент времени мы можем считать её постоянной в пределах данной клетки. Таким образом, суммирование в последнем слагаемом (1) ведется по всем соседним клеткам, которые вносят вклад в общий диффузионный поток. Учитывая дискретность поля концентрации, поток вещества может быть записан следующим образом:
J jj = a L ij ( Ci - C j ) .
Здесь J ij – поток вещества С из клетки i в клетку j ; α – коэффициент диффузии; L ij – длина участка границы между i - и j -клетками (см. рис. 2). Нелинейная функция Φ( С ) в уравнении (1) может описывать различные биохимические процессы в клетках.
Вообще говоря, уравнение вида (2) позволяет описывать не только подпитку клеток кислородом, но и, например, процессы генной регуляции. Например, в работе [10] была выведена модель регуляции, контролирующая циркадианные ритмы в клетках, которые в свою очередь регулировали биомеханические свойства среды эпителия. Таким образом, уравнение (или система уравнений) вида (1) позволяет описывать процессы реакции и переноса в ядрах клеток, задавая самый мелкий масштаб явления в ткани эпителия. Обратная связь с биомеханикой среды работает здесь следующим образом: химический сигнал С может служить непосредственной командой для изменения локальных механических свойств ткани. С другой стороны, механика клетки (изменение формы, деление, интеркаляция) меняет условия для формирования сигнала C и может как усилить, так и ослабить его. Таким образом, формируется хемоэластичность среды.
Эластичная потенциальная энергия всей эпителиальной ткани задается следующим уравнением:
П = 1 у (И( L - L о)2 + n( A - A о)2) , (3)
2 cells где L - периметр; A - площадь клетки, а суммирование ведется по всем клеткам рассматриваемой системы. Первое слагаемое в выражении (3) описывает действие сил, стремящихся сократить периметр каждой клетки до минимального L0 (периметр гексагональной ячейки), а второе - представляет собой сопротивление клетки действию сил растяжения и сжатия со стороны среды и стремление клетки сохранить свою среднюю площадь Aо. Коэффициенты эластичности среды ц и п являются важными параметрами модели, определяющими свойства деформации среды.
Эпителиальная ткань эволюционирует посредством перемещения узлов клеток-многоугольников. Вектор механической силы, действующей на j -й узел (узлы многоугольника отмечены на рис. 2 точками), определяется обычным для механики образом - как градиент потенциальной энергии по радиусу-вектору узла (3):
F =-^Л
j dRj где Rj - радиус-вектор j-го узла. Смещение узлов приводит к деформации клетки, а следовательно - к изменению её площади и периметра.
Обсудим уравнение движения для клеток. В случае здорового эпителия клетки включены в общий пласт, связаны с соседями десмосомами и не могут перемещаться по ткани. В этом случае ткань представляет собой классическое деформируемое твердое тело, и уравнения движения для такой среды не нужно. Однако клеточная среда обладает свойством внезапного ожижения, когда клетки получают команду двигаться, а вся ткань в целом проявляет черты жидкости. Например, такая ситуация складывается при ранении ткани. В этом случае механизм генной регуляции в ядрах клеток, получая сигнал о ранении, включает синтез протеинкиназы МАРК (mitogen-activated protein kinase - митоген-активируемая протеинкиназа). Последняя, распространясь от клетки к клетке в виде волны, производит ожижение клеточного слоя, примыкающего к ране. Десмосомы размыкаются, клетки приходят в движение, а края раны начинают смыкаться, пытаясь восстановить целостность покрытия органа или всего организма [24]. Другими примерами, где движение клеток играет важную роль, являются морфогенез (рост органа или организма под действием химических сигналов) и распространение опухоли (раковые клетки принципиально не связаны десмосомами с пластом здоровой ткани и могут перемещаться в ней). Можно заметить, что движение клеток происходит при значительном сопротивлении среды, так как проницаемость этой среды весьма низкая. Здесь прямая аналогия с фильтрацией жидкости в пористой среде, и совсем не случайно существует много примеров моделирования клеточной ткани с помощью модели эффективной пористой среды [20]. Сопротивление движению жидкости при её фильтрации через пористую среду приводит к использованию при описании закона Дарси, который игнорирует инерционные слагаемые в уравнении Навье–Стокса [25]. Таким образом, мы приходим к выводу, что наиболее приемлемым аппаратом для описания движений в клеточной ткани является механика Аристотеля, а не Ньютона. В уравнении движения Аристотеля (как и в законе Дарси) силы напрямую определяют скорость движения объекта. Учитывая это замечание, уравнение для смещения узлов клетки запишем в следующем виде:
V = R = K F H(| F I - F0 ) ,
где H – функция Хэвисайда; K – коэффициент мобильности с подходящей размерностью; F 0 – параметр, определяющий критическую силу, ниже которой узел остаётся неподвижным. Последний параметр гарантирует, что любое локальное движение в среде начинается, если внешняя сила превышает некоторый порог. Это необходимо для придания общей устойчивости и определенной инертности ткани.
Уравнение (5) было записано в минимальном виде. На самом деле, кроме потенциальных механических сил (4), которые мы учли в правой части (5), нужны ещё какие-то предположения о причинах движения клеток. По сути, уравнение (5) описывает эволюцию мертвой ткани, которая пассивно реагирует на внешнее механическое воздействие. Живая клеточная ткань получает химические команды на внезапное движение клеток. Эти команды поступают с уровня ядер клеток, где протекают процессы генной регуляции. Один такой пример в случае ранения ткани был приведён выше. В математической биологии такие силы называют активными . С точки зрения некоторых физиков, такая сила нарушает третий закон динамики, так как движение ткани выглядит как акт внезапного самодвижения в среде. Дискуссия по поводу активных сил продолжается, и заинтересованный читатель сам может окунуться в эту тематику [6]. Позиция авторов по этому поводу следующая: движение биологической ткани не может быть сведено к действию только физических сил, потому что это означало бы механистическое восприятие жизни. При моделировании здесь должен использоваться принцип дополнительности Нильса Бора [4], сформулированный ещё для квантовой механики. Биологические и физические понятия должны дополнять друг друга, но не сводиться друг к другу. Таким образом, активная сила может рассматриваться как продукт жизнедеятельности клетки – сложнейшего образования природы. При математическом моделировании таких сложных объектов неизбежно приходится вводить в рассмотрение существование неких процессов, выходящих за пределы физики. Всю совокупность этих сложных процессов мы формально можем описать в модели путем введения в рассмотрение некой эффективной активной силы.
Кроме активных сил в уравнение (5) можно добавить и другие взаимодействия, которые описывают различные биологические явления. Например, в работе [29] было рассмотрено явление поляризации клеточной ткани, под которой понимается выстраивание цитосклета каждой клетки ткани таким образом, чтобы соответствовать общему паттерну (рисунку) этой ткани. В результате в модели в уравнении (5) в правой части должна быть задана сила, которая учитывает это групповое вазимодействие клеток, при котором соседи заставляют каждую клетку ориентировать свой цитоскелет в соответствии с общим правилом [24].
Для клеток эпителия в модели предполагается, что вероятность p деления клетки зависит от количества её узлов:
p = p о q
n - 6
где p 0 и q – параметры задачи. В случае q > 1 деление клеток с большим числом узлов предпочтительно, хотя наиболее выгодной формой клетки остаётся многоугольник в виде гексагональной ячейки. Сам процесс деления происходит так, как это показано на рис. 3 справа: в многоугольнике строится отрезок, соединяющий середины самых длинных в клетке противоположных сторон. Новая клетка заносится в реестр и начинает свою индивидуальную эволюцию в ткани эпителия. При этом она наследует от материнской клетки мгновенные значения химических и механических полей в момент деления. Таким образом, алгоритм имитирует митотическое деление клетки.
Следующее важное свойство реального эпителия – это процесс интеркаляции. В здоровом эпителии, клетки которого связаны между собой с помощью десмосом, это явление происходит не часто. Процесс интеркаляции необходим для ослабления давления, оказываемого на клетку в ткани, для снятия локальных напряжений, а также для всей ткани в случае её существенной структурной перестройки [16]. Простейший алгоритм интеркаляции может быть записан следующим образом:
P int = 1
Алгоритм (7) срабатывает, если перемычка между клетками становится меньше критического значения l 0 (рис. 3). В целом, механизмы пролиферации и интеркаляции позволяют клеткам модели динамически менять форму и размер за счёт изменения количества вершин многоугольника и их взаимного перемещения под действием внешних сил (см. рис. 3). Таким образом, каждая клетка в модели испытывает ряд хемомеханических воздействий, под влиянием которых она эволюционирует со всей системой. Обратная связь между процессами реакции–диффузии в клетках (1, 2) и механикой клеточной ткани, описываемой уравнениями (3)–(7), может быть задана путем установления функциональной зависимости величин μ, η, F 0 , p 0 , q , и l 0 с
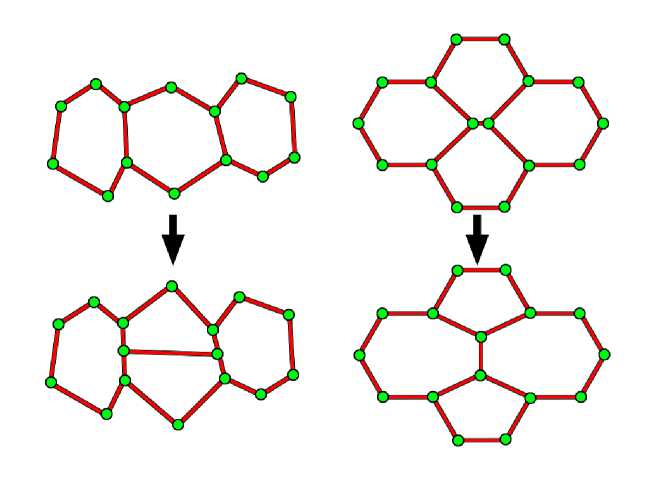
Рис. 3. Процессы деления (слева) и интеркаляции (справа)
концентрациями C . В этом случае ткань начинает проявлять свойства хемоэластомера, механические свойства которого изменяются под влиянием биохимических процессов в клетках и ядрах клеток.
Численное моделирование динамической системы (1–7) может быть выполнено с помощью подходящей конечно-разностной схемы, в которой временной шаг уравнений реакции–диффузии (1) должен быть синхронизирован с шагом механической подсистемы (5).
Выше описана лишь общая методология построения дискретной математической модели клеточной среды с индивидуальной динамикой. Для каждой конкрентной задачи базовая модель должна быть существенно доработана и изменена с учетом условий задачи. Разработанную модель можно классифицировать как дискретную сложную систему, которая включает индивидуальную динамику отдельных элементов, а также групповые эффекты коллективного поведения.
Примеры имитационного моделирования
Однородный рост клеточной массы
Первый пример иллюстрирует однородный рост клеточной массы из зародыша, который состоит из небольшого числа гексагональных клеток (рис. 4). Расчет химической динамики (1), (2) не производится. Клетки делятся согласно распределению вероятностей (7) со следующими значениями параметров: p 0 = 10 -6 , q = 1,4. Выбор значений обусловлен тем, что после каждого акта деления система должна успеть отрелаксировать, снимая избыточные напряжения в ткани за счет интеркаляций. Из рис. 4 видно, что клетки в центральной части имеют меньшую площадь по сравнению с клетками на периферии. Их сравнительно малый размер обусловливается избыточным давлением со стороны массы клеток. Форма клеток, которые находятся на краях расчётной; области, обусловлена отсутствием давления со стороны среды. Однако давление со стороны растущей ткани растягивает самые
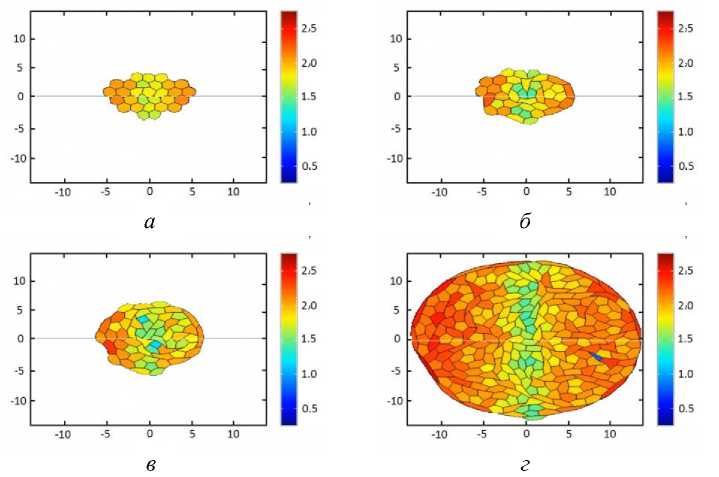
Рис. 4. Однородный рост клеточной массы из зародыша. Представлено поле площади клеток в моменты времени: а – 100; б – 1500; в – 3000; г – 4500, где время имеет безразмерную величину

крайние клетки ткани. В представленном расчёте наглядно показано, что в ходе эволюции клетки могут принимать форму практически любого многоугольника. Гистограмма на рис. 5 показывает, как меняется распределение клеток по форме многоугольников со временем. Наибольшее число клеток имеет шесть вершин, что в среднем контролируется распределением (6). Появление клеток с числом вершин меньше четырёх невозможно, так как такая клетка (с тремя вершинами) будет испытывать существенное давление со стороны других клеток и, в конце концов, схлопываться.
Моделирование морфогенеза
Как известно, процесс морфогенеза контролирует организованное пространственное распределение клеток во время эмбрионального развития организма. Для морфогенеза характерен сбор клеток в кластеры для того, чтобы максимизировать контакт с клетками того же типа. При эмбриональном развитии происходят несколько событий клеточного дифференцирования, когда мезенхимальные (М) клетки меняют свой фенотип и становятся эпителиальными (Э), и обратно. Процесс происходит под воздействием морфогенов, стимулирующих морфогенез. Как правило, морфогены синтезируются при генной регуляции во время формирования организма [17].
На рис. 6 представлен расчёт, имитирующий морфогенез. В качестве начального состояния задана однородная прямоугольная полоса клеточной ткани, составленная из правильных гексагональных клеток. В представленном расчёте принимается гипотеза о том, что клетки прошли стадию агрегации и в начальный момент времени уже находятся в нужных кластерах. Клетки, находящиеся в кластерах, начинают испускать морфогены, которые в свою очередь запускают процессы интенсивного клеточного деления. Здесь деление клеток связано с величиной концентрации морфогена C и зависимостью от площади A :
p = H ( C - C * ) H ( A - A * ) k . (8)
Здесь С* и A* – пороговые значения концентрации и площади, выше которых начинается деление клеток; k – нормировочный коэффициент. Параметры в (8) подобраны таким образом, что клетки в кластерах на каждом шаге по времени испытывали деление с вероятностью 10%. Клетки, которые находятся в кластере с низким содержанием морфогенов, испытывают деление в соответствии с алгоритмом (6), который обсуждался выше для ординарных условий.
Ввиду наличия свободных границ сверху и снизу расчётной области начинает образовываться структура, похожая на позвонки. Из полей периметра (см. рис. 6, справа) видно, что клетки, которые делятся во внутренней области растущего кластера, испытывают сильное давление со стороны среды, так как перераспределение напряжений и движение клеток осуществляются медленнее, чем происходит их деление. Со временем находящиеся внутри кластера клетки перестают делиться из-за достижения критических размеров A *. Таким образом, основной вклад в рост структуры осуществляют фронтальные клетки кластеров, что хорошо согласуется с экспериментальными наблюдениями. На самом деле процесс морфогенеза управляется на фронте ткани с помощью специальных клеток роста (клетки-почки или budding cells ), поэтому реальный рост ткани проиходит более эффективно, чем это показано на рис. 6.
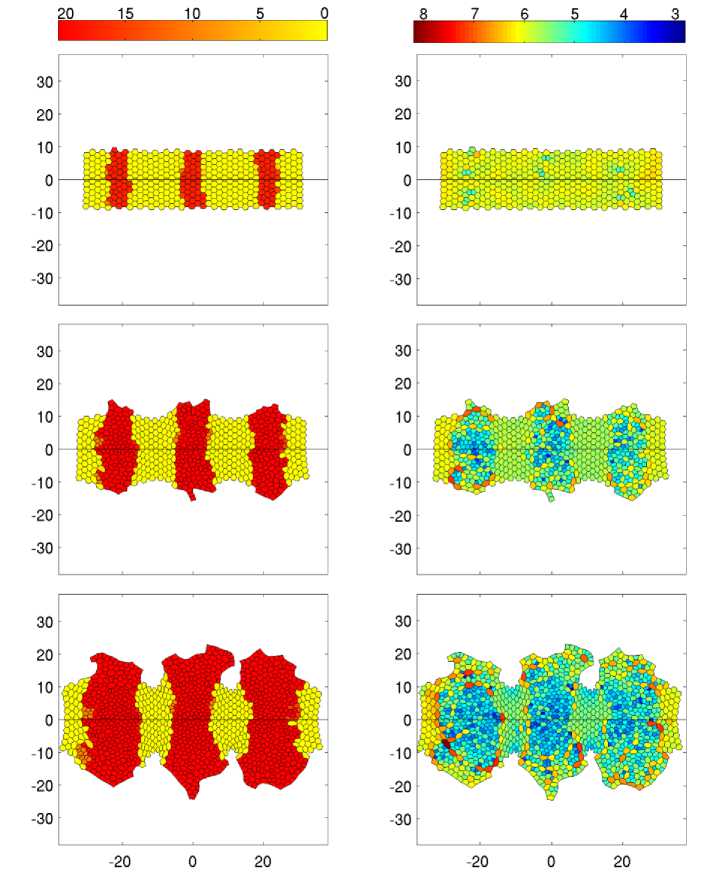
Рис. 6. Рост клеточной ткани, стимулируемый и управляемый локальной концентрацией морфогена. Моменты времени 5, 100, 200 представлены сверху вниз, время имеет безразмерную величину. Слева представлено поле концентрации морфогена в клеточных кластерах, справа - поле периметра клеток. Параметры расчёта: A о = 6^3/5; A* = 6^2/5; C* = 10,0; п = 1,0; ц = 0,0; l 0 = 0,3
Стоит отметить, что при численном моделировании однородного роста клеточной массы из зародыша (см. рис. 4) и роста клеточной ткани, стимулируемого и управляемого локальной концентрацией морфогена (см. рис. 6), мы не проводили прямое сравнение с реальной ситуацией гистогенеза. Однако ставилась задача формального воспроизведения этих процессов в численном моделировании, которое не нарушало бы самых общих законов функционирования ткани и не приводило бы к априори абсурдным результатам. Полученные результаты наглядно продемонстрировали способность предложенной математической модели симулировать динамические изменения в ткани, что включает в себя локальную перестройку положения клеток, снятие избыточного давления в массе, движения границ ткани.
Моделирование роста папиллярной раковой опухоли
Характерный паттерн развития папиллярной карциномы реализуется в случае сниженной подвижности опухолевых клеток по сравнению со здоровыми клетками. За подвижность раковых и здоровых клеток отвечает параметр интеркаляции l 0 . Мы идентифицируем эту структуру как папиллярную опухоль, сравнивая её с гистологическими примерами [21]. Для неё характерны длинные, тонкие и извилистые образования из раковых клеток, которые продолжают соединяться с основным «ядром» опухоли. Аналогичный паттерн пассивно формируется здоровой тканью, так что две ткани врастают друг в друга, и граница между ними становится вытянутой и извилистой. Типичная эволюция папиллярной структуры со временем показана на рис. 7, где были использованы следующие значения параметров, задающие интеркаляцию соответственно раковым и здоровым клеткам: l 0can = 0,1, l 0norm = 0,4. Можно заметить, что из-за инвазивной природы папиллярной структуры и высокой подвижности клеток здоровой ткани в зоне роста опухоли механическое напряжение в ткани эпителия невелико. Этот вывод становится особенно очевидным, если тщательно изучить площадь клеток (рис. 7): видно, что размер клеток плавно меняется, а переход между здоровой тканью и опухолью не показывает резких контрастных изменений. Абсолютное большинство клеток не испытывает чрезмерного давления со стороны окружающей среды, поскольку здоровые клетки быстро адаптируются к изменениям, вызванным растущей опухолью из-за их высокой подвижности.
Повышенную подвижность клеток здоровой ткани, прилегающих к опухоли, можно интерпретировать следующим образом. Известно, что опухоль должна подавлять для успешной инвазии экспрессию генов, кодирующих синтез кадгерина и интегрина [1]. Таким образом, связи между здоровыми клетками уменьшаются в узком пограничном слое. Фактически карцинома инициирует ЭМ-переход в граничном слое здоровых клеток и «разжижает» его, чтобы облегчить дальнейшую инвазию. Такое поведение может быть достигнуто различными способами: например, путем явной активации молекулярного механизма, блокирующего синтез кадгерина и интегрина, что приводит к качественному изменению химико-механических свойств клеточной ткани. Однако можно поступить и по-другому: чтобы сделать здоровые ткани более рыхлыми и проницаемыми, можно задать увеличенное значение параметра интеркаляции l 0norm для здоровых клеток, непосредственно примыкающих к опухоли. Этот подход эффективно моделирует процесс разрыва связей между здоровыми клетками, регулируемыми на генном уровне.
Анализируя рис. 7, можно заметить интересную нитевидную субструктуру, которая состоит из клеток с большими площадями. Если типичная величина площади для клетки внутри опухоли составляет около 2, то клетки нитевидной субструктуры имеют площадь больше на 20–30%. Так как вдоль нитей площадь клеток в среднем равна площади клеток на периферии ткани (рядом со свободной границей), то напряжения вдоль нитей практически отсутствуют. Интересно отметить, что нитевидные структуры образуются как раковыми, так и здоровыми клетками (см. рис. 7) под влиянием динамически изменяющихся напряжений в среде. По мере роста опухоли нитевидные субструктуры не исчезают, а представляют собой долгоживущие и развивающиеся образования. Со временем могут появиться новые
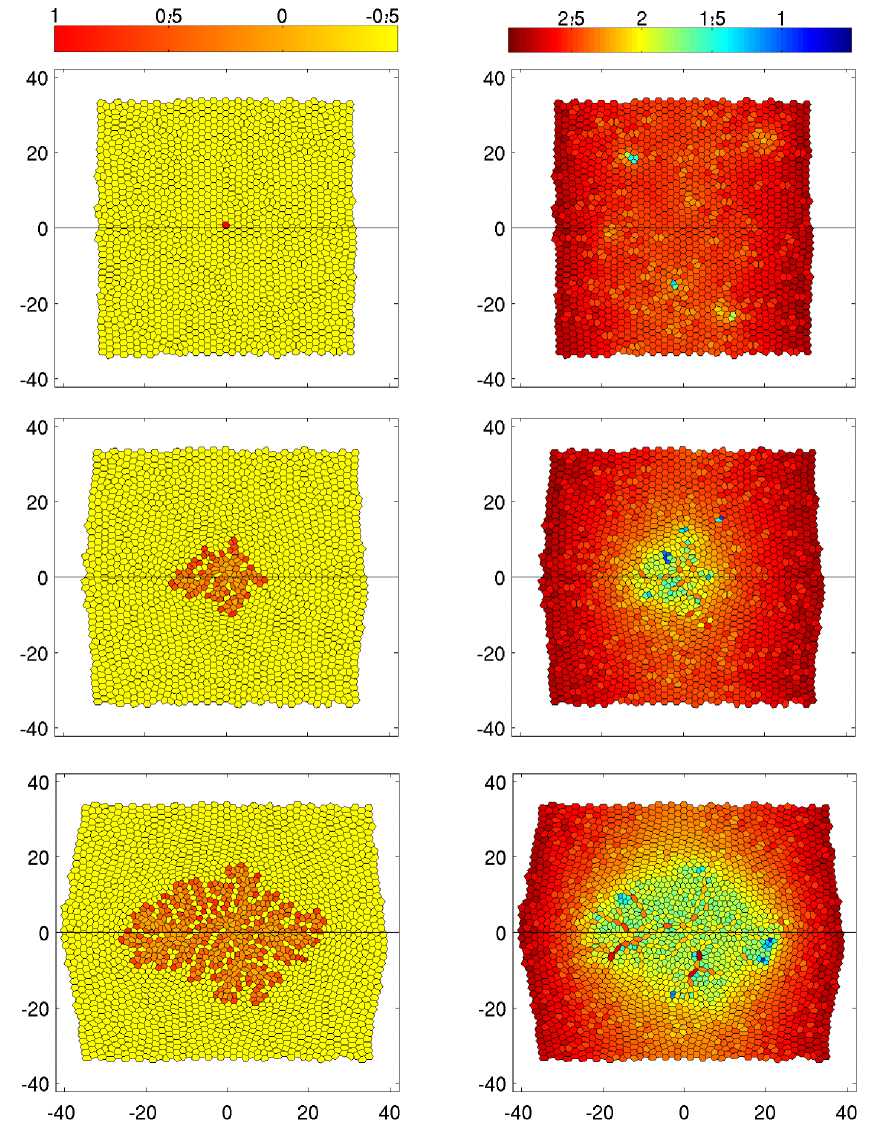
Рис. 7. Эволюция папиллярной карциномы. Моменты времени 5, 60, 120
представлены сверху вниз, время имеет безразмерную величину. Слева представлено поле индекса ЭМ-перехода раковой клетки, справа – поле площади клеток. Параметры расчёта для здоровых и раковых клеток: A = 6√3/5; η = 4,5; μ = 0,0
ветви, но старые также продолжают развиваться. Всё это говорит о том, что нитевидные структуры являются важной особенностью биомеханики клеточной ткани, находящейся под действием внешнего давления.
Заключение
В работе обсуждается методология построения дискретной математической модели эпителиальной ткани, состоящей из большого числа клеток. Каждая клетка описывается деформируемым многоугольником и обладает индивидуальным поведением. Рассмотрены примеры численного расчета конкретных задач математического моделирования, среди которых однородный рост ткани из небольшого зародыша, управляемый морфогеном рост ткани, развитие папиллярной опухоли в здоровой клеточной ткани.
Благодарности
Данная работа была финансово поддержана Министерством науки и высшего образования Российской Федерации (грант № FSNM-2020-0026).
Список литературы Математическое моделирование роста эпителиальной ткани
- Захаров А.П., Брацун Д.А. Синхронизации циркадианных ритмов в масштабах гена, клетки и всего организма // Компьютерные исследования и моделирование. - 2013. - Т. 5, № 2. - C. 255-270.
- Колобов А.В., Полежаев А.А. Влияние случайной подвижности злокачественных клеток на устойчивость фронта опухоли // Компьютерные исследования и моделирование. - 2009. - Т. 1, № 2. -С. 225-232.
- Красняков И.В., Брацун Д.А., Письмен Л.М. Математическое моделирование роста карциномы при динамическом изменении фенотипа клеток // Компьютерные исследования и моделирование. -2018. - Т. 10, № 6. - С. 879-902.
- Розенфельд Р. Развитие принципа дополнительности // Нильс Бор. Жизнь и творчество. - М., 1967. -С. 61-87.
- Штейн А.А., Юдина Е.Н. Математическая модель растущей растительной ткани как трёхфазной деформируемой среды // Российский журнал биомеханики. - 2011. - Т. 15, № 1. - С. 42-51.
- Ahmed W.W., Fodor E., Betz T. Active cell mechanics: Measurement and theory // Biochimica et Biophysica Acta (BBA) - Molecular Cell Research. - 2015. - Vol. 1853, iss. 11, part B. - P. 3083-3094.
- Basan M., Elgeti J., Hannezo E. et al. Alignment of cellular motility forces with tissue flow as a mechanism for efficient wound healing // Proc. Natl. Acad. Sci. - 2013. - Vol. 110, no. 7. - P. 2452- 2459.
- Bratsun D., Volfson D., Tsimring L.S., Hasty J. Delay-induced stochastic oscillations in gene regulation // Proc. Natl. Acad. Sci. - 2005. - Vol. 102, No. 41. - P. 14593-14598.
- Bratsun D.A., Krasnyakov I.V., Pismen L.M. Biomechanical modeling of invasive breast carcinoma under a dynamic change in cell phenitype: collective migration of large groups of cells // Biomech. Model. Mechanobiol. - 2020. - Vol. 19. - P. 723-743. DOI: 10.1007/s10237-019-01244-z
- Bratsun D.A., Merkuriev D.V., Zakharov A.P., Pismen L.M. Multiscale modeling of tumor growth induced by circadian rhythm disruption in epithelial tissue // J. Biol. Phys. - 2016. - Vol. 42, no. 1, - P. 107-132.
- Chauviere A., Preziozi L., Verdier C. Cell Mechanics: From Single Cell-Based Models to Multi-Scale Modeling. - London: Press Chapman and Hall/CRC, 2010. - 482 p.
- Chavey D. Tilings by regular polygons - II: A catalog of tilings // Computers & Mathematics with Applications. - 1989. - Vol. 17. - P. 147-165. D0I:10.1016/0898-1221(89)90156-9
- Chung C.A., Lin T.H., Chen S.D., Huang H.I. Hybrid cellular automaton modeling of nutrient modulated cell growth in tissue engineering constructs // J. Theor. Biol. - 2010. - Vol. 262, Issue 2. - P. 267-278.
- Dilao R. Mathematical Models of Morphogenesis // ITM Web of Conferences. - 2015. - Vol. 4. - P. 01001.
- Drasdo D., Loeffler M. Individual-based models to growth and folding in one-layered tissues: Intestinal crypts and early development // Nonlinear Anal. - 2001. - Vol. 47, iss. 1. - P. 245-256.
- Guillot C., Lecuit T. Mechanics of epithelial tissue homeostasis and morphogenesis // Science. - 2013. -Vol. 340, iss/ 6137. - P. 1185-1189. DOI: 10.1126/science. 1235249
- Little S.C., Tkacik G., Kneeland T.B. et al. The formation of the bicoid morphogen gradient requires protein movement from anteriorly localized mRNA // PLoS Biol. - 2011. - Vol. 9, iss. 3. - P. e1000596. DOI: 10.1371/journal.pbio.1000596
- Lober J., Ziebert F., Aranson, I.S. Collisions of deformable cells lead to collective migration // Sci. Rep. -2015. - P. 9172. D0I:10.1038/srep09172
- Markov M.A., Markov A.V. Computer simulation of the ontogeny of organisms with different types of symmetry // Paleontol. J. - 2014. - Vol. 48, no. 11. - P. 1-9.
- Netti P.A., Baxter L.T., Boucher Y. et al. Macro- and microscopic fluid transport in living tissues: application to solid tumors // AIChE J. - 1997. - Vol. 43, iss. 3. - P. 818-834.
- Pal S.K., Lau S.K., Kruper L. et al. Papillary carcinoma of the breast: an overview // Breast Cancer Res. Treat. - 2010. - Vol. 122. - P. 637-645.
- Ranfta J., Basan M., Elgeti J. et al. Fluidization of tissues by cell division and apoptosis // Proc. Natl. Acad. Sci. - 2010. - Vol. 107, no. 49. - P. 20863-20868.
- Ruben I., Reinaldo R.-R., Fernando V.-R. et al. Tumor growth modelling by cellular automata // Mathematics and Mechanics Complex Systems. - 2017. - Vol. 5, no. 3-4. - P. 239-259.
- Salm M., Pismen L. M. Chemical and mechanical signaling in epithelial spreading // Phys. Biol. - 2012. -Vol. 9, no. 2. - P. 026009-026023.
- Seetha N., Raoof A., Kumar M.M.S., Hassanizadeh M.S. Upscaling of nanoparticle transport in porous media under unfavorable conditions: Pore scale to Darcy scale // J. Contam. Hydrol. - 2017. - Vol. 200. -P. 1-14.
- Simpson M.J., Landman K.A., Hughes B.D. Distinguishing between directed and undirected cell motility within an invading cell population // Bull. Math. Biol. - 2009. - Vol. 71. - P. 781-799.
- Tozluoglu M., Tournier A.L., Jenkins R.P. et al. Matrix geometry determines optimal cancer cell migration strategy and modulates response to interventions // Nat. Cell Biol. - 2013. - Vol. 15. - P. 751-762.
- van Leeuwen I.M., Mirams G.R., Walter A. et al. An integrative computational model for intestinal tissue renewal // Cell Prolif. - 2009. - Vol. 42. - P. 617-636.
- Viktorinova I., Pismen L., Aigouy B., Dahmann C. Modeling planar polarity of epithelia: the role of signal relay in collective cell polarization // J. R. Soc. Interface. - 2011. - Vol. 8. - P. 1059-1063.
- von Neumann J. Theory of self-reproducing automata (edited and completed by Artur W.Burks). - London, Press: University of Illinois, 1966. - 388 p.
- Zakharov A.P., Pismen L.M. Reshaping nemato-elastic sheets // Eur. Phys. J. E. - 2015. - Vol. 38, no. 7. -P. 75. DOI: https://doi.org/10.1140/epje/i2015-15075-6


