Математическое моделирование с учётом ограничений и исследование оптимальной конфигурации оптической стереосистемы, состоящей из двух плоских зеркал и видеокамеры

Системы технического зрения в настоящее время широко применяются для решения многих практических задач: неразрушающий контроль качества деталей и материалов, создание 3D-моделей реальных объектов, биометрические системы распознавания, автономные роботы и др. Существует несколько способов восстановления 3D-структуры наблюдаемой сцены.

Первый способ — использование источников лазерного излучения (лидаров) и времяпролетных (ToF-) камер. Принцип их работы основан на измерении времени движения световых лучей. Важнейшее преимущество лидаров и ToF-камер — они позволяют восстановить 3D-структуру наблюдаемой сцены без дополнительных сложных алгоритмов калибровки сенсоров и анализа сенсорных данных. Недостаток: информация о текстуре и цвете объектов сцены недоступна, если дополнительно не используются обычные видеокамеры. Кроме того, стоимость лидаров может быть достаточно высокой.

Второй способ — использование структурированной подсветки: излучатель проецирует на объекты некоторый паттерн известной конфигурации, а видеокамера выполняет съемку подсвеченных объектов. Поскольку конфигурация паттерна и взаимное расположение видеокамеры и излучателя известны, то можно восстановить 3D-координаты точек, на которые попадает паттерн. Подобные решения значительно дешевле лидаров, но требуют наличие алгоритмов детектирования на изображении тех пикселей, на которые попала подсветка. В условиях неконтролируемого освещения эта задача может быть нетрививальной. Кроме того, могут быть восстановлены 3D-координаты только тех точек, на которые попала подсветка, т.е. получить так называемое плотное стерео (dense stereo) становится затруднительным.

Если первые два способа относятся к так называемому активному стереозрению, то третий способ — к пассивному. Он основан на съемке сцены несколькими фото- или видеокамерами с разных ракурсов. Если объекты неподвижны, то также может использоваться вариант, когда одна камера выполняет снимки с разных ракурсов (англ. structure from motion — структура из движения). Подобные решения дешевле лидаров, сохраняют информацию о тектуре и цвете объектов, менее требовательны к освещению, по сравнению с решениями на основе структурированной подсветки. Пассивное стереозрение более скрытно, поскольку использование активных систем может быть обнаружено сторонним наблюдателем. Кроме того, видеокамеры имеют обычно более высокое быстродействие (FPS, Frames per Second — количество кадров в секунду), чем лидары и ToF-камеры.

Работа многокамерных систем основана на решении задачи стереосопоставления (stereo correspondence problem): поиск соответствия между пикселями изображений, выполненных с разных ракурсов. И здесь, конечно, следует заметить, что данная задача является одной из самых сложных в компьютерном зрении и не имеет универсального алгоритма ее решения.

Для восстановления 3D-структуры сцены также используются катадиоптрические системы, в состав которых входят видеокамера и комбинация преломляющих и отражающих элементов. На одной светочувствительной матрице создается сразу несколько изображений. Проблема стереосопоставления остается актуальной, но для получения стереоснимков достаточно одной видеокамеры. Следствие этого факта: уменьшение общей стоимости элементов оптической системы и отсутствие в необходимости синхронизации камер.

Пример задачи, в которой использование подобных оптических систем являются фактически единственным возможным вариантом: измерение уровня вибрации на рабочих поверхностях приборов для воспроизведения звука. Такая задача исследуется, к примеру, в статье [1] . В этой задаче необходимо построить 3D-модель вибрирующей поверхности, и стереозрение имеет ряд преимуществ перед другими способами решения задачи: возможность проводить измерения по всему рабочему полю и низкая чувствительность к окружающему акустическому шуму. Но возникает необходимость использования высокоскоростных камер, которые достаточно дороги. Однако, при использовании системы зеркал и единственной камеры общая стоимость всей системы радикально уменьшается.

Если присутствуют только преломляющие элементы, то такая система называется диоптрической, а если только отражающие элементы, то катоптрической. Диоптрические системы исследуются, к примеру, в работах [2, 3] , в данном случае используются призмы. Катоптрические системы разделяются по типу используемых зеркал, плоских или криволинейных.

С криволинейными зеркалами можно добиться более широких углов обзора, но более заметными становятся геометрические искажения, особенно по краям зеркал. Данная работа является продолжением наших исследований катоптрических систем с плоскими зеркалами, результаты предыдущих исследований изложены в статьях [4 –6] . В статье [6] изложен аналитический обзор публикаций подобных оптических систем, здесь мы ограничимся его краткой версией.

Системы, в которых только одно плоское зеркало, наиболее простые [7] , но имеют малый угол обзора, для решения этой проблемы зеркало делают подвижным [8 –10] . В работе [11] предложена математическая модель формирования изображений в системе из камеры и одного зеркала (плоского, конического, сферического, параболического, эллиптического или гиперболического), авторы выполнили оценку пространственного разрешения оптических систем и оценку уровня размытия, вызванного расфокусировкой. В качестве примеров работ по математическому моделированию трехзеркальных систем можно привести статьи [7 , 12 –14] .

В трехзеркальных системах на одну часть фотоматрицы проецируются лучи, отразившиеся от одного зеркала, а на другую часть матрицы — отразившиеся от двух других зеркал. На таком принципе основана и оптическая система, которая исследовалась, например, в статьях [15 , 16] : 9 зеркал организованы в виде двух пирамид, расположенных друг напротив друга. Четырехзеркальные системы исследовались, к примеру, в статьях [17 –22] . Отдельно можно выделить работы, посвященные созданию панорамных стереоизображений с использованием множества зеркал [23, 24] . Наконец, имеются работы (например, [25] ), в которых описываются катадиоптрические системы, содержащие и зеркала, и преломляющие элементы: например, два плоских зеркала и дихроичный фильтр.

Данная работа посвящена двухзеркальным системам. Хотя имеется достаточно много статей по таким системам, нужно заметить, что в части работ принимается ряд допущений, сужающих область применения предложенных математических моделей. Например, в работе [26] одно из зеркал располагается параллельно плоскости изображения камеры, а в работе [27] зеркала располагаются симметрично относительно оптической оси камеры.

Однако рассматриваются и более общие случаи. Так в статьях [28, 29] выведены уравнения эпиполярных ограничений, предложен алгоритм вычисления фокальной длины системы линз, вычислен угол обзора стереосистемы. В работе [30] описана система из двух плоских зеркал и RGB-D камеры, два зеркала позволяют следить за обстановкой перед мобильным роботом и за ним. В статье [31] предложен алгоритм вычисления угла между зеркалами и вычисления фундаментальных матриц, связывающих положения и ориентации камеры относительно зеркал. На основе двух или трех зеркал можно построить калейдоскопическую систему, таким системам посвящены, к примеру, работы [32, 33].

Обзор показал, что в существующих математических моделях катоптрических систем с плоскими зеркалами используется небольшое количество параметров: в частности, для двухзеркальных — чаще всего только угол обзора и размер стереобазы. Но практически не затрагиваются следующие аспекты:

• ^•    реальные образцы оптических систем имеют определенные габариты и массу, и могут быть ограничения на максимально возможные размеры оптической системы. Например, на беспилотный летательный аппарат или на подвижный робототехнический комплекс невозможно поставить слишком большую катоптрическую систему.

• ^•    может иметь место проблема двойного отражения. Если в одном зеркале отражается другое зеркало, то в результате на изображении появятся неинформативные области.

• ^•    в зеркалах могут отражаться области, наблюдение которых следует избегать. Например, в зеркалах может отражаться видеокамера или элементы конструкции, которые входят в оптическую систему.

• ^•    рабочая зона двухзеркальной оптической системы образована пересечением полей зрения двух виртуальных камер. Восстановить 3D-координаты можно только для тех объектов, которые попали в эту зону. В наиболее простых случаях рабочая зона имеет форму треугольника, один из его углов и будет углом обзора оптической системы. Но какова будет конфигурация рабочей зоны при различных расположениях зеркал относительно видеокамеры — эта проблема своего всестороннего анализа пока не получила.

В нашей предыдущей работе [6] была предложена математическая модель катоптрической системы с двумя плоскими зеркалами, в которую входит величина стереобазы, размеры зеркал, учитывается возможность двойного отражения, возможность отражения в зеркалах видеокамеры, а также учитываются общие габариты оптической системы. Выполнена постановка задачи условной оптимизации, которая позволяет найти конфигурацию оптической системы с заданными характеристиками и минимальными размерами.

В настоящей работе мы исследуем конфигурацию рабочей зоны оптической системы в зависимости от положения зеркал и дополним оптимизационную задачу еще одним набором ограничений, которые задают размеры этой зоны.

1.    Полученные ранее результаты

На рисунке 1 приведена иллюстрация модели оптической стереосистемы

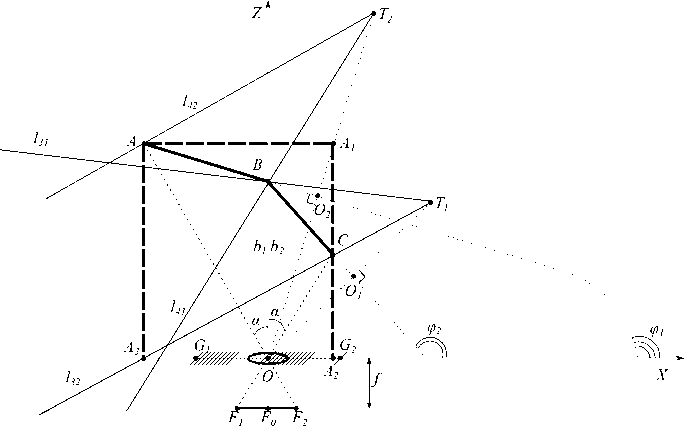
Рисунок 1. Модель оптической стереосистемы из видеокамеры и двух плоских зеркал из двух плоских зеркал, подробное ее описание доступно в работах [5, 6]. Используется вид сверху, начало координат (точка O) расположено в оптическом центре камеры, ось OX направлена вправо от камеры, ось OZ — вперед (оптическая ось), а ось OY направлена вниз. Центр объектива камеры совпадает с началом координат, объектив изображен в виде тонкой линзы.

В реальных камерах чаще всего линз несколько, но здесь мы используем математическую модель «камера-обскура» и перспективную проекцию. Фокальная длина линзы равна f, отрезок F 1 F 2 соответствует фотоматрице видеокамеры, плоскости обоих зеркал параллельны оси OY . Отрезки AB и BC соответствуют плоскостям зеркал, вместе они перекрывают все поле зрения камеры и соединяются в точке B, которая лежит на оси OZ. Отрезки AB и BC лежат на прямых с уравнениями z = tan (ф 1 ) x + b 1 и z = tan (ф ₂ ) x + b ₂ , здесь ф 1 и ф ₂ — углы между прямыми и положительным направлением оси OX , ф 1,2 G [0,п].

Пусть ось OZ делит угол обзора камеры пополам, т.е. центр фотоприемника (точка F ₀ ) лежит на оси OZ , или же близко к оси: для большинства современных камер это условие выполняется. Если угол обзора обозначить как 2а, то AAOB = ABOC = а. Положения левой и правой виртуальных камер обозначены точками T 1 и T 2 , рассчет их координат представлен в статье [6] . Нетрудно убедиться, что эти точки являются отражением точки O относительно зеркал. Поле зрения левой виртуальной камеры образовано лучами l 31 и l 32 , и правой виртуальной камеры — лучами l 41 и l 42 .

Сделаем три замечания относительно разработанной математической модели.

• (1)    Все параметры видеокамеры фиксированы и не входят в состав оптимизируемых параметров. В данной задаче требуется знать только один параметр камеры — ее горизонтальный угол обзора 2а. Разработка и проектирование собственной видеокамеры — намного более трудная задача, по сравнением со случаем, когда используется готовая видеокамера, и требуется рассчитать только конфигурацию отражающих и/или преломляющих элементов.

• (2)    дисторсия на снимках либо незначительна, либо устранена программными методами (камера при этом должна быть заранее откалибрована).

• (3)    а <  ^п/2, в противном случае мы имеем дело со сверхширокоугольными камерами, которые в данном исследовании не рассматриваются.

Опишем постановку оптимизационной задачи, которая была ранее исследована и численно решена в статье [6]:

• (1)                  Ф 1 >^П / ^ + ^а,ф 1 >^ф 2 ^,ф 1,2 G ( ^п / 2^,п ] ,

• (2)                 base (Ф 1 , Ф 2 , b) := 2bsin (ф 1 - Ф 2 ) >  T min ,

b sin a

• (3)                      L 1 ^(ф 1 , ^{b) :}=                    <  L 10 ,

— cos (Ф 1 — a)

b sin a

• ⁽⁴⁾                    L 2 ^(ф 2 ^,ь):=                  ^ L 20 ,

— cos (Ф 2 + a)

• ^{(5)                            ф} 1 <  ^2ф 2 ^{— П} / 2,

• (6)                  ( X c — X a ) <  wbox, Z a <  hbox,

• (7)          ( Ф 1 < ³ⁿ / ₄ ) OR (( Ф 1 >  ³ⁿ / 4 ) AND (U 41 <  — s i ) ) ,

• (8)    ( Ф 2 <  ( ³ⁿ / 4 — ^a / 2 )) OR (( Ф 2 > ( ³ⁿ / 4 — ^a / 2 )) AND ( u 32 <  — S 1 )) ,

• (9)    F ^(ф 1 , ^ф 2 , b) =^{2 ((}X C ^(ф 1 , ^{b) —} X A ^(ф 2 , ^b)) + Z A ^(ф 2 , ^b)) ^ mill .

• 2.    Случай Аф < ^а / 2

Поясним (1) : если ф 1 <  ^п /2 + а, то прямая AB не будет пересекаться с лучом OA ; если ϕ 1 ≤ ϕ 2 , то поля зрения виртуальных камер не будут пересекаться (обнаружено экспериментально); если ф 1 ,₂ <  ^п/2, то камера будет наблюдать заднюю поверхность зеркала. Условие (2) задает ограничение на величину стереобазы: она должна быть не менее заданного значения T _min . Условия (3) и (4) задают ограничения на ширины зеркал: ширина левого зеркала не превосходит величину L 10 , а ширина правого зеркала — величину L 20 . При условии (5) не наблюдается двойное отражение. Выражение (6) задает ограничения на размеры габаритного прямоугольника AA 1 A 2 A 3 , который ограничивает оптическую систему; ширина прямоугольника не превосходит значения wbox, а высота — значения hbox. При условиях (7) и (8) в зеркалах не отражается конструкция видеокамеры. Здесь через u ij обозначена абсцисса точки пересечения луча l ij и оси OX , а s 1 — длина отрезка G 1 O , здесь G 1 G 2 — отрезок, который в предыдущей статье был определен как «запрещенная зона» — область, которая не должна отражаться в зеркалах, она соответствует габаритам конструкции видеокамеры. Выражение (9) определяет функцию, которую необходимо минимизировать: периметр прямоугольника AA 1 A 2 A 3 .

Исследование оптической системы из камеры и двух плоских зеркал 63

Было проведено моделирование различных конфигураций двухзеркальной системы в среде Maple. В итоге было обнаружено, что конфигурация рабочей зоны зависит от значения ∆ϕ = ϕ 1 - ϕ 2 и угла обзора видеокамеры 2α. Оказалось, что при ∆ϕ < ^α₂ рабочая зона (см. рисунок 2) имеет наиболее простой вид, она заключена между лучами l 31 и l 41 .

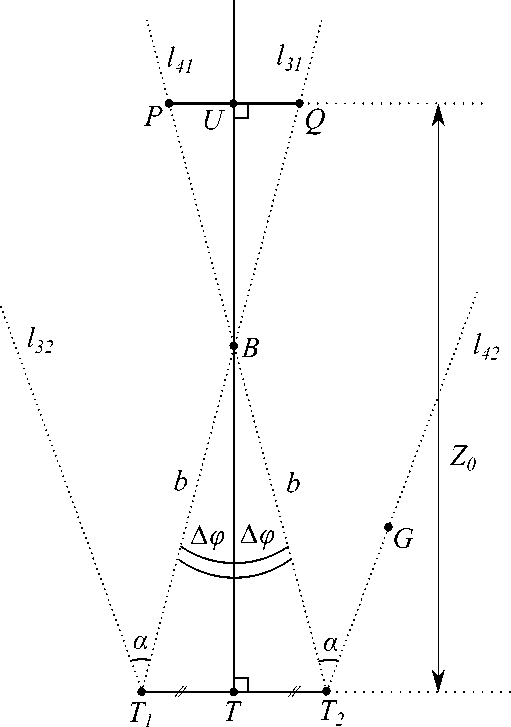
Рисунок 2. Расчет рабочей зоны в случае А ф <  ^а/ 2

Поскольку T 1 B = T 2 B = b, то △ T 1 BT 2 — равнобедренный. Тогда если точка T — середина T 1 T 2 , то TB — высота и медиана △ T 1 BT 2 . Поскольку величина стереобазы T 1 T 2 = 2b sin Аф, то sin ZTBT 2 = ^TT 2 / BT₂ = sin Аф, откуда ZTBT 2 = ZTBT 1 = Аф, а TB = b cosAф.

Таким образом, угол обзора оптической стереосистемы, который расположен между лучами 1 з1 и 1 41 , равен Аф. На наш взгляд, угол обзора не является здесь достаточно информативной характеристикой оптической системы, поскольку не содержит полной информации о размерах рабочей зоны. Пусть от оптической системы требуется, чтобы рабочая зона простиралась на расстояние Z 0 от пары виртуальных камер (рисунок 2) . И также требуется, чтобы ширина рабочей зоны (отрезок PQ ) на этом расстоянии составляла не менее чем H 0 . Конкретные значения Z 0 и H 0 могут быть выбраны, исходя из особенностей задачи и особенностей детектируемых объектов. Такой задачей может быть, например, автономная навигация подвижного робота, детектирующего препятствия и целевые объекты с помощью стереозрения, или восстановление 3D-структуры сцены в задаче стереомикроскопии или неразрушающего контроля. Расстояние Z 0 назовем эффективной дальностью.

Введем функцию f ₁ , которая определяет длину отрезка PQ (используем тот факт, что ZUBQ = ZT 1 BT ):

f 1 (Аф, b) = 2 (UT - TB) • tan ZUBQ =

2 (Z 0 — b cos Аф) • tan Аф = 2Z 0 • tan Аф — 2b • sin Аф.

В итоге мы можем записать следующее условие на размеры рабочей зоны (здесь и далее для более компактной записи опустим аргументы функций f i , поскольку у всех функций они совпадают и равны Аф и b): (11) ( Аф<% ) AND (f i >  H o ).

Моделирование также показало, что при Аф <  ^а/ 2 прямые, на которых лежат лучи l 31 и l 42 , пересекаются за виртуальными камерами. Рассмотрим, в каком случае эти прямые будут параллельны. Если они параллельны, то ZBT 1 T 2 = п — ZT 1 T 2 G = п — (ZT 1 T 2 B + ZBT 2 G), откуда Аф = ^а / ₂. Аналогичный результат можно получить, если рассмотреть лучи l 32 и l 41 .

Исследование оптической системы из камеры и двух плоских зеркал 65

• 3.    Случай Аф G [ ^а / 2, а ]

В случаях, когда значение ∆ϕ превосходит ^α₂, но не превосходит α, конфигурация рабочей зоны имеет более сложный вид, представленный на рисунке 3. Она состоит из треугольника BB 1 B 2 и области, расположенной выше отрезка B ₁ B ₂ между лучами l ₃₂ и l ₄₂ . В точке B ₁ пересекаются

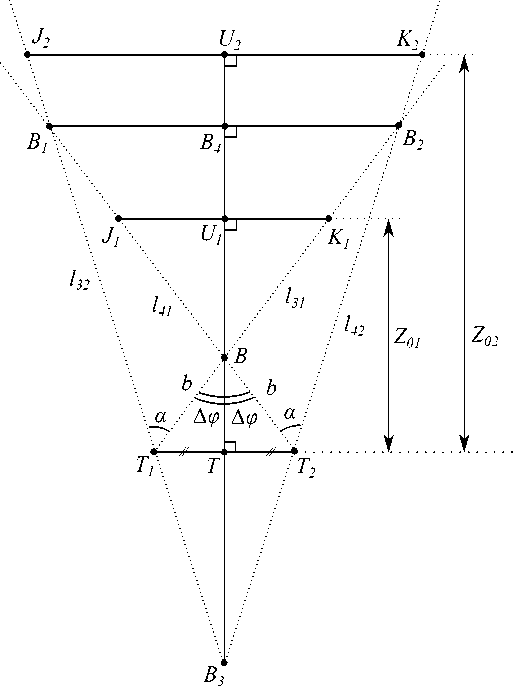
Рисунок 3. Расчет рабочей зоны в случае ∆ϕ ∈ α 2, α лучи l32 и l41 , а в точке B2 — лучи l31 и l42 . В точке B4 пересекаются прямые B1B2 и TB.

Нетрудно убедиться, что рассчет ширины рабочей зоны будет выпол- няться по разному для эффективных расстояний, больших либо меньших чем длина отрезка T B4 . Вначале выведем формулу для вычисления его длины, воспользовавшись теоремой синусов и свойствами вертикальных углов:

TB 4 = TB + BB 4 = b cos Лф + BB 1 • cosZB 4 BB 1 = = (b + BB 1 ) • cos Лф,

ZB 1 BT 1 = n - ZT 1 BT 2 = п - 2Лф,

ZBB 1 T 1 = п - ZB 1 BT 1 - ZBT 1 B 1 = 2Лф - а,

BB1   _   BT1      ^в _ b sin а sin ZBT1B1 = sin ZBB1T1 ^   1 = sin (2Лф - а) ’

/ 2 (Лф, а) = TB 4 = b cosЛф f 1 + . sin        .

sin (2Лф - а) J

Пусть эффективное расстояние Z o = Z o1 не превосходит длину отрезка TB 4 , тогда ширина рабочей зоны (отрезок J 1 K 1 ) вычисляется по формулам из предыдущего раздела. Получаем следующее условие:

• (13)         ( ^а / ₂ <  Лф <  а ) AND (Z o <  / 2 ) AND (/ 1 >  H o ).

Если же Z o = Z o2 больше чем TB 4 , то ширина рабочей зоны (отрезок J 2 K 2 ) зависит от длины отрезка U 2 B 3 :

U 2 B 3 = U 2 T + TB 3 = Z o + TT 2 • cot ZTB 3 T 2 =

= Z _o + b sin Лф • cot ZTB 3 T 2 ,

ZTT 2 B = ^п / ₂ - ZTBT 2 = ^п / ₂ - Лф,

• (14)       ZTT 2 B 3 = п - ZTT 2 B - ZBT 2 B 2 = ^п / ₂ + Лф - а,

ZTB 3 T 2 = ^п / ₂ - ZTT 2 B 3 = а - Лф, / з (Лф, b) = J 2 K 2 = 2U 2 B 3 • tan ZTB 3 T 2 =

= 2Z o • tan (а - Лф) + 2b • sin Лф.

В результате получаем следующее логическое выражение

• (15)         ( ^а / ₂ <  Лф <  а ) AND (Z o >  / 2 ) AND (/ 3 >  H o ).

• 4.    Случай Аф G ( а,^п / 2 )

Результаты моделирования показали, что при увеличении угла Лф точка B 3 все дальше удаляется от виртуальных видеокамер и в какой–то момент уходит в бесконечность: прямые l 32 и l 42 становятся параллельными. Условие параллельности можно записать в виде выражения ZB 2 T 2 B 1 + ZBB 1 K 1 = п. Поскольку ZBB 1 T 1 = 2Лф - а, то несложно убедиться, что параллельность возникает при Лф = а.

Исследование оптической системы из камеры и двух плоских зеркал 67

При дальнейшем увеличении угла Аф точка пересечения прямых 1 з2 и l ₄₂ находится уже перед виртуальными камерами (точка B ₅ на рисунке 4) ,

B 5

l41

J3

U 3

B 1

K 3

B 4

B 2

l32

b

α ∆φ

B     ^l42

b ∆φ α

T 1

^______(

T

^-к • ■

T 2

l31

Z03

Рисунок 4. Расчет рабочей зоны в случае ∆ ϕ ∈ α, ^π₂

а рабочая область оптической системы теперь становится областью ограниченного размера — четырехугольник BB 1 B 5 B 2 .

Как и в предыдущем разделе, ширина рабочей зоны зависит от того, превосходит ли расстояние Z 0 длину отрезка T B 4 . Если не превосходит, то этот вариант уже был рассмотрен ранее, и мы получаем следующее логическое выражение:

• (16)         ( а < Аф < ^п / ₂ ) AND (Z o <  / 2 ) AND (f i >  H o ).

В противном случае (расстояние Z0 = Z03 на рисунке 4) необходимо, чтобы обеспечивалось условие Z0 ≤ T B5 . Вычислим длину отрезка TB5 ZTT2B5 = ZTT2B + ZBT2B5 = п/2 - Аф + а,

• (17)                    TB 5 = TT 2 • tan ATT 2 B 5 ,

  / 4 (Аф, b) = TB 5 = b • sin Аф • cot (Аф — а).

а затем определим ширину рабочей зоны J 3 K 3 :

T 1 T 2 WB 1 B 2 ^ AU 3 K 3 B 5 = ATT 2 B 5 ,

• (18)               J 3 K 3 = 2 (TB 5 — U 3 T ) • cot AU 3 K 3 B 5 ,

  / з1 (Аф, b) = 2Z o • tan (а — Аф) + 2b • sin Аф = / 3 (Аф, b) .

В итоге получаем следующее логическое выражение:

• (19)  (а < Аф < ^п/2) AND (Zo > /2) AND (/4 > Zo) AND (/3 > Ho).

5.    Постановка и решение задачи условной оптимизации для поиска оптимальной конфигурации оптической системы

Мы получили ограничения на размеры рабочей зоны оптической системы в виде набора выражений (11), (13), (15), (16), (19). Эти выражения добавляются в модель (1)–(9), которая разработана в предыдущей статье. Соответствующие изменения были внесены в разработанную ранее программу для численного решения задачи условной оптимизации с использованием программного пакета SciPy . Использовался метод differential_evolution из модуля optimize для поиска глобального минимума скалярной функции вида F X⃗ при заданном наборе ограничений вида ⃗bl ≤ F⃗ X⃗ ≤ ⃗bu . Этот программный метод базируется на эвристическом алгоритме дифференциальной эволюции.

Программа доступна в github-репозитории . Отметим особенность программной реализации обновленной модели. Пять логических выражений (11) , (13) , (15) , (16) , (19) не могут все одновременно быть истинными (например, не может быть оба истинными выражение (Аф < ^а/2) и выражение (а <  Аф <  ^п /2)), поэтому оптимизационная задача фактически разбивается на пять отдельных независимых подзадач, в каждую из которых входят выражения (1) – (9) и по одному из пяти новых выражений. В процессе работы программы какие-то из пяти подзадач могут не иметь решения (соответствующие системы неравенств окажутся несовместными), а среди решения остальных подзадач выбирается то решение, при котором значение целевой функции будет наименьшим.

В таблице 1 приведены примеры расчета конфигурации оптической системы для различных значений параметра H 0 .

Таблица 1. Расчет конфигурации оптической системы при различных значениях параметра H 0

H 0 (см)	F (см)	ϕ 1 (рад)	ϕ 2 (рад)	b 1 , 2 (см)	AB (см)	AC (см)	AA 1 (см)	A 1 A 2 (см)	∆ ϕ (рад)
—	20,6	3,00	2,29	5,3	3,0	2,6	4,6	5,7	0,72
20	35,9	3,00	2,60	8,9	4,9	4,0	8,3	9,7	0,40
30	41,6	2,95	2,60	10,1	5,7	4,6	9,6	11,2	0,35
40	49,0	2,92	2,62	11,7	6,8	5,3	11,2	13,2	0,30
50	—	—	—	—	—	—	—	—	—

Здесь F — минимум целевой функции (периметр AA ₁ A ₂ A ₃ ), AB и BC — размеры левого и правого зеркал, w х h — размеры короба AA ₁ A ₂ A ₃ . Значения остальных параметров были взяты из предыдущей статьи, а именно: угол а = 26, 75 ° = 0, 467 рад., расстояние Z o = 100 см минимальное значение стереобазы T min = 7 см, максимально возможная ширина обоих зеркал L 10 = L 20 = 10 см, максимально допустимые размеры короба AA 1 A 2 A 3 равны wbox х hbox =15 х 15 см, а длина отрезка G 1 O = s 1 = 1 , 5 см. Вторая строка таблицы демонстрирует расчеты для случая, когда параметр H 0 не учитывается. Для случая H 0 = 50 см решение не было найдено.

По таблице видно, что если необходимо увеличить ширину рабочей зоны, то угол между зеркалами будет уменьшаться, а габариты оптической системы — увеличиваться (при условии, что все остальные параметры остаются неизменными). Например, если необходимо рассчитать конфигурацию двухзеркальной оптической системы для ее установке на подвижном роботе (летающем или ездящем), то потребуется найти баланс между габаритами оптической системы (слишком большую систему зеркал разместить не получится) и требуемой шириной рабочей зоны. А ширина зависит от особенностей той задачи, для решения которой планируется использовать возможности стереозрения: например, от размера наблюдаемых целевых объектов, трехмерную структуру которых требуется восстановить.

Заключение

Выполнена модификация ранее разработанной математической модели катоптрической системы, состоящей из двух плоских зеркал и обеспечи- вающей получение стереопар изображений с помощью единственной видеокамеры. Модель учитывает практические аспекты, возникающие при проектировании подобных систем: ограничения на размер зеркал, проблема двойного отражения, наблюдение запрещенных областей, общие габариты оптической системы. В рамках данной работы в модель добавлены ограничения, которые учитывают конфигурацию рабочей зоны оптической системы, рабочая зона образована пересечением полей зрения двух виртуальных камер. Алгоритм численного решения задачи условной оптимизации был написан с использованием возможностей программного пакета SciPy.

Полученные результаты могут быть использованы для проектирования катоптрических стереосистем различного назначения: например, для их установки на подвижных автономных роботах, для визуального контроля качества изготовленных деталей на конвейере или для анализа характеристик рабочих поверхностей акустических систем. Во всех трех случаях критична синхронизация полученной стереопары снимков, что и обеспечивается подобными катоптрическими системами. В дальнейшем планируется использовать предложенный подход к исследованию трехзеркальных и четырехзеркальных катоптрических стереосистем.