Математическое моделирование шлифовального станка с учетом взаимодействия упругой, тепловой подсистем и рабочего процесса

обработки. До настоящего времени, тепловые и динамические процессы при шлифовальной обработке исследовались раздельно. Но при использовании предельных режимов резания и повышении требований к точности обработки постоянные времени этих процессов в зоне резания становятся сравнимыми. Поэтому динамическое поведение технологического оборудования можно предсказать только с учетом комплексного воздействия тепловых и упругих процессов.

Для исследований в данной работе использована математическая модель термодинамической системы шлифовального станка, учитывающая взаимодействие упругих, тепловых явлений и процесса резания. Для построения математической модели использован метод электрической аналогии, который позволяет отразить как тепловые, механические, так и процессы другой физической природы.

Станок большей частью представляет собой сложную структуру и через статические и динамические свойства, а точнее через передаточные функции процесса шлифования, оказывает значительное влияние на колебания при шлифовании. К колебательной системе (рис. 1) при плоском шлифовании принадлежит подсистема инструмента, в которую входит шлифовальный круг, подсистема заготовки и упругая система станка. Характеристики шлифовального круга, его профиль, а также кинематика процесса влияют на склонность к колебаниям и вибрациям. Заготовка через свою геометрию, статическую и динамическую жесткости также влияет на процесс колебаний.

В модели упругая система станка представлена в виде отдельных сосредоточенных масс, соединенных жесткостями и обладающих определенным демпфированием колебаний. Для сокращения числа степеней свободы и упрощения модели некоторые связи между соседними элементами принимаются абсолютно жесткими, если ожидаемое перемещение по соответствующим координатам мало влияет на относительные смещения шлифовального круга и стола.

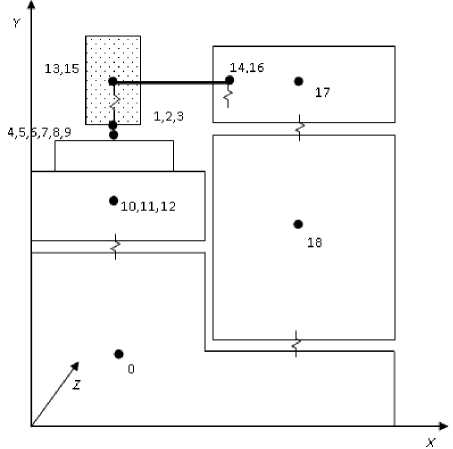
Рис. 1. Расчетная схема плоскошлифовального станка

В качестве сосредоточенных масс выделены: станина и основание станка (точка 0); стол (точки 10,11,12); колонна со шлифовальной бабкой (точка 18); гильза шлифовального шпинделя (точка 17); шлифовальный круг (точки 1, 2, 3). Шпиндель шлифовального круга представлен как стержень, закрепленный в гильзе шпинделя и испытывающий изгибные деформации (точки 13,15,14, 16).

Шлифование, как процесс пластического деформирования и разрушения материалов детали и круга, занимает промежуточное положение между резанием резцом [1, 2] (инструментом с определенной режущей кромкой) и трением. При моделировании динамики процесса резания при шлифовании процесс резания будем отображать в виде полной линейной модели [1, 2], так как процесс микрорезания зерна схож с процессом резания резцом. При этом процессы микрорезания зерен, находящихся в контакте с заготовкой, представим в виде некоторого совокупного процесса.

Абразивные и алмазные круги, применяемые при шлифовании, являются инструментами со стохастическим (вероятностным) расположением множества элементарных режущих зерен. В месте расположения каждого из зерен с материалом заготовки выделяется теплота, возникающая в процессе срезания отдельной стружки. Расположение этих локальных источников тепловыделения на поверхности контакта между заготовкой и кругом в связи со стохастическим размещением зерен непрерывно меняется во времени. Это приводит к выравниванию температур на всей контактной поверхности заготовки. Эти особенности процесса шлифования позволяют при отображении тепловых процессов ориентироваться на схематизированное зерно с некоторыми усредненными геометрическими параметрами и условиями работы.

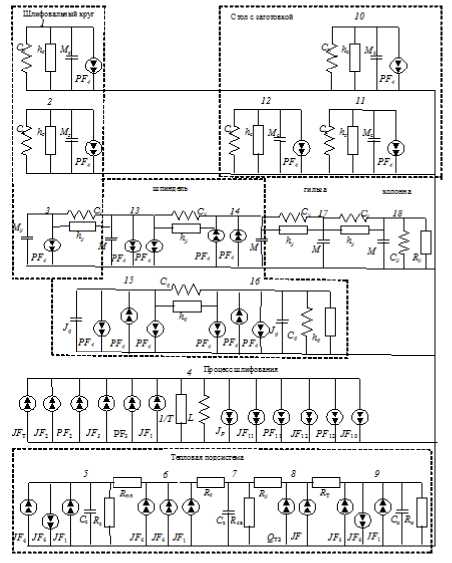
Рис. 2. Эквивалентная схема термодинамической системы шлифовального станка при учете резания в виде полной линейной модели:

C z , C y , C x , C _ф - приведенные жесткости соответствующих подсистем; h z , h y , h x - приведенные коэффициенты демпфирования механических подсистем; R _с, R _пп, R z , R y , R _св, R ТЗ , R _и,- коэффициенты сопротивления тепловому потоку в зоне шлифования; M z , M y , M x , J_ф - приведенные инерционные параметры подсистем; L - условная податливость процесса резания единичной величины; T P -постоянная времени стружкообразования; J P - номинальная сила резания, определяемая припуском ; Q _ТЗ -источник тепла от трения по задней поверхности зерен; PF , JF - фиктивные источники, отражающие взаимодействие подсистем

Для отображения тепловых процессов в локальной области, прилежащей к зерну, будем использовать систему тел и элементарных источников согласно [3, 6, 7]. Теплота от каждого элементарного источника распределяется между всеми телами, участвующими в процессе. Представим это распределение в виде итоговых потоков теплообмена между инструментом, заготовкой и стружкой [3-7]. Используя метод прямой аналогии и сделанные допущения, получаем следующую эквивалентную схему (рис. 2), которая отражает динамику упругих и тепловых процессов при шлифовании. Для исследований используется оригинальная компьютерная программа, использующая в качестве исходных данных эквивалентную схему. Математическая модель тепло-динамической системы шлифовального станка при плоском шлифовании, построенная по эквивалентной схеме, представляет собой систему обыкновенных дифференциальных уравнений с постоянными коэффициентами:

d2zA dzA

+ℎ   +   +=0

z dt2 z dt z 1 z d2x7dx

+ℎ  ++=0

dt2dt d2y3 (dy3

+ℎ

-

^) + С_у(у₃ - у₁₃) + к_уР dt /

=0

(Z0^ dz_± dx₂              dx₃

ℎ   +ℎ    +ℎ    +    +ℎ    +    +

^T dt ^Pz dt ^Px dt ^{Px 2 р}у dt ^pv^³

+

ТР dt

dz-\ n dx^ i

++ℎ   +ℎ   + z dt x dt x

+

dyi2

+ℎ     +     + 0

py dt y

+ dt v

-

ПП

-

+

-

-

ПП

'5

-

^-07 ПП

-

(

-

)—=0

+ ПП

'6

-

-

⁽ᴨ + ᴨ⁾ —

-ᴨ = 0

d0₇ / ⁺

++ св

R

ТЗ

'8

-

R

z

'7

-

=0

R”⁶⁹ ТЗ

-

ТЗ = ТЗ

+И

ТЗ

d 0g / ⁺

И

ТЗ    И

dl

-

^И —

^И -

=0

M1Q

d2z10

dt2

dz-y П

+ℎ  +  +=0

z dt

Mu

d2xT1

dt2

dx-i i

+ℎ ++=0

dt

Ml2

d2yi2

dt2

dy12

+ℎ ++=0

-(

-

) -ℎ

-

d2Vi3

+ vv U /              vv U

+      +

++(

-

)+ℎ

-

=0

dt /

J13

d2Vi3

dt2

+

-

+      +

-

+(

-

h

)+ℎ

^Vis

dt

-

d^Pi6

dt

(

-

Zi

)-ℎ

d-Vis

dt

-

dVie

d2Vi6

dt

dt2

+

dyi6

+     +      +      +    + ℎ =0

-(

-

, , (dy14

)-ℎ

-

+ dt /

d2yM

dt2

+

+(

-

)+ℎ

-

=0

dt /

-(

-

) -ℎ

-

+ dt /

d2yi4

dt2

+

dyis

+    + ℎ    =0

где Θ 5,6,7,8,9 – средние температуры характерных элементов исходной системы шлифовальной обработки соответственно: средняя температура стружки; средняя температура на передней поверхности зерна (температурой резания); средняя температура в теле режущего зерна; средняя температура на задней поверхности зерна; средняя температура на поверхности изделия в зоне резания; C z , C y , C x , C φ – приведенные жесткости соответствующих подсистем; h z , h y , h x – приведенные коэффициенты демпфирования механических подсистем; R с , R пп , R z , R y , R св , R ТЗ , – коэффициенты сопротивления тепловому потоку в зоне шлифования; M z , M y , M x , J φ – приведенные инерционные параметры подсистем; L – условная податливость процесса резания единичной величины; Т P – постоянная времени стружкооб-разования; J P – номинальная сила резания, определяемая припуском ; Q ТЗ – источник тепла от трения по задней поверхности зерен; k Px , k Py – коэффициенты резания по соответствующим координатам; h Px , h Py , h Pz – коэффициенты демпфирования резания по соответствующим координатам; k x , k y , k z – коэффициенты, определяемые проекциями силы резания на соответствующие оси; K di , K di , K dv - коэффициенты, учитывающие долю теплоты деформации, переходящей в изделие, пропорционально тангенциальной составляющей силы резания, нормальной составляющей силы резания и скорости резания;

ИИИ

K d i^, K d i^, K dv - коэффициенты, учитывающие долю теплоты деформации, переходящей в стружку, пропорционально тангенциальной составляющей силы резания, нормальной составляющей силы резания и скорости резания; K ni , к n2 , K nv - коэффициенты, учитывающие долю теплоты трения стружки по передней поверхности, переходящей в стружку, пропорционально тангенциальной составляющей силы резания, нормальной составляющей силы резания и скорости резания; C С , С З , С И – учитывают эквивалентные теплоемкости стружки, зерна и круга.

Полученная математическая модель описывает основные теплодинамические процессы при шлифовании. Она обладает достаточной гибкостью и универсальностью, позволяет отображать нюансы тепловых и механических упругих процессов при различных условиях обработки, в том числе исследовать проблему отвода тепла со смазочно-охлаждающей жидкостью. В то же время ее компактность позволяет встраивать ее в более сложные системы.

С помощью предложенной модели были рассчитаны температуры, возникающие в процессе плоского шлифования без охлаждения деталей из закаленной до HRC64 быстрорежущей стали периферией круга ПП200*20*75 с зернами эльбора ЛО63/50, связкой Б1, концентрацией зерна Ко=100%. Результаты были сопоставлены с экспериментальными данными, полученными В.В. Щипановым в Тольяттинском политехническом институте, и с расчетными данными А.Н. Резника. Сопоставление результатов показало, что влияние скорости резания и скорости заготовки на температуру резания в расчетных и экспериментальных закономерностях достаточно близки, расхождения не превышают 10%. В математической модели были использована схематизация и допущения при теплофизическом анализе, предложенные А.Н. Резником. Хорошее согласование расчетов с экспериментальными значениями показывает целесообразность использования подобной схемы.

Предложенная методика и модель могут быть использованы при исследовании особенностей теплодинамических процессов в шлифовальных станках при резании. Они позволяют изучать влияние разнообразных факторов на тепловые процессы в процессе шлифования, на относительные смещения шлифовального круга и заготовки из-за появляющихся в процессе динамических явлений, которые влекут за собой значительные отклонения геометрической формы, изменения температуры в зоне резания и, соответственно, микроструктуры поверхностного слоя.

Является целесообразным предсказание вибрационных колебаний при шлифовании с помощью данной математической модели, которая позволяет получить динамические характеристики при динамически нестабильном процессе шлифования без дорогостоящих натурных испытаний. Модель, базирующаяся на чисто геометрических связях, не может передать передаточные характеристики процесса шлифования в полной мере. Необходима модель, связывающая воедино кинематику, упругопластические процессы внедрения зерен, силы резания, тепловые процессы в зоне резания, физические свойства системы шлифовальный станок / заготовка.

Температура резания определяется не только процессами распределения тепла в системе, но и динамическими процессами в системе шлифовальный станок / заготовка и динамикой самого процесса шлифования. При определенных сочетаниях параметров обработки возникают колебания температуры резания, как при врезании шлифовального круга, так и при резонансах режимах работы.