Математическое моделирование состава поликомпонентных продуктов

Современные условия развития науки приводят к необходимости проводить комплексное исследование объекта. Экспериментом является вид деятельности, предпринимаемой в целях научного познания, открытия объективных закономерностей и состоящий в воздействии на изучаемый объект посредством специальных инструментов и прибо- ров. Модельным экспериментом является особая форма эксперимента, характерной чертой которого служит использование действующих материальных моделей в качестве специальных средств экспериментального исследования.

Объекты и методы исследований

Объектом исследования является плавленый сыр, методы исследований – имита- ционное моделирование с последующей экспериментальной оценкой адекватности математической модели.

При проектировании состава поликом-понентных продуктов используется растительное сырье, обладающее повышенной биологической ценностью, что позволяет получать композиции, характеризующиеся улучшенным витаминным, минеральным, углеводным и аминокислотным составом по сравнению с отдельно взятыми компонентами; при этом возможно более тонкое управление процессом формирования продуктов.

Наиболее изученным разделом математического моделирования является линейное программирование, для решения задач которого разработан целый комплекс эффективных методов, алгоритмов и программ.

Плавленые сыры - продукты с многокомпонентным составом, технология которых позволяет, внося новые ингредиенты, моделировать не только вкус, цвет и запах, но и консистенцию и биологическую ценность продукта. Во многих университетах ведутся работы по автоматизации процесса проектирования состава поликомпонентных смесей и продуктов.

При создании поликомпонентных смесей заданного сырьевого состава и повышения используют объектно-ориентированные подходы. Особое внимание при проектировании продуктов в последнее время уделяется корректированию биохимического состава продукта для повышения пищевой и биологической ценности. [1]

Результаты и их обсуждение

Рассмотрим моделирование состава плавленого сыра. Его белковую и жировую основу составляют сычужные сыры и продукты молочного происхождения, витаминноминеральный комплекс - добавки растительного происхождения.

• 1.    Составление рецептуры. Обозначим через x 1, x 2, x 3, x 4, x 5, x 6, x 7 соответственно искомый удельный вес включения в состав продукта каждого вида сырья. Тогда задачу можно записать в следующем виде: найти искомые значения x 1, x 2, x 3, x 4, x 5, x 6, x 7, при которых

F ( x ) = min{а1 x 1 + а2 x 2 + а3 x 3 + а4 x 4 + а5 x 5 + а6 x 6 + а7 x 7},                        (1)

где аi - энергетическая ценность каждого вида сырья, при соблюдении следующих условий:

• 1)    наличие в вырабатываемом продукте сухих веществ не более 50%.

s1 x 1 + s2 x 2 + s 3x 3 + s 4x 4 + s 5x 5 + s 6x 6 + s 7 <0.5,                                     (2)

где si - содержание сухих веществ в каждом виде сырья

• 2)    наличие в вырабатываемом продукте не более 30% жиров,

• 2.    Математическая обработка результатов эксперимента. Статистическая обработка данных выполнялась путем определения стандартного отклонения (± SD) в трех повторностях. Для уменьшения числа опытов в планах второго порядка в настоящее время повсеместно реализуется идея композиционного планирования. Суть этой идеи состоит в том, что сначала осуществляют план полного факторного эксперимента 2 порядка, а затем, если полученное уравнение не может быть признано работоспособным, добавляют к этому плану некоторое количество специальным образом расположенных, так называемых «звездных» точек и опыт в центре эксперимента. По результатам двухфакторного эксперимента можно составить уравнение, в котором помимо линейных членов будет член, учитывающий эффект парного межфакторного взаимодействия:

z1 x 2 + z2 x 3 + z4 x 4 + z5 x 5 + z6 x 6 + z7 x 7< 0,3,                                 (2а)

где zi - содержание жира в каждом виде сырья.

Выражение для получения единицы продукта имеет вид x 1 + x 2 + х 3 + x 4 + x 5 + х 6 + х 7 = 1.   (3)

y = b o + b l Х 1 +b 2 X 2 +Ь 12 Х 1 X 2 (4)

Такая возможность имеется в связи с тем, что эксперимент по плану ПФЭ2² (полный факторный эксперимент полиномом 2 степени) насчитывает N = 2² = 4 опыта, а число коэффициентов N' в линейном уравнении всего три. Рассматривая метод наименьших квадратов (МНК) применительно к плану ПФЭ2², надо невязки формулировать с учетом эффекта межфакторного взаимодействия и в конечном счете - формулу для расчета независимой оценки эффекта парного межфакторного взаимодействия b₁₂:

г _ S u = 1 ^ 1u ^ 2u V

012 =     ^                        (5)

Линейные коэффициенты в линейном уравнении целиком характеризуют влияние исследуемого фактора на процесс (табл. 1).

Таблица 1 - Влияние исследуемых факторов на процесс парного межфакторного взаимодействия ингредиентов

Х	Х1	Х2	Х3
6	-	+	+
7	+	-	+
8	+	+	+
9	-R	0	0
10	+R	0	0
11	0	-R	0
12	0	+R	0
13	0	0	-R
14	0	0	+R
15	0	0	0

Этот план симметричный Eu=i X;u = 0 и линейно ортогональный Еи=г xiuXjU = 0. Иными словами в уравнении y=b0+b1x1+b2x2+b3x3+b12x1x2+b13x1x3+b23 x2x3+b11x1 +b22x2 +b33x3 (6)

независимыми от всех других оценок будут лишь оценки линейных коэффициентов и эффектов парных межфакторных взаимодействий:

У ^N 1 г²

Й — Ьи = 1Xluyu. L _ i = VN у2  • ^ij =

L u = 1 ^X iu

ZN  „ „  — и = 1 XtuXtj уи

Z ^N=1 ( ^Xiu^Xij ) 2

Оценки свободного члена и квадратичных эффектов в уравнении (7), полученном МНК по симметричному плану, должны рассчитываться по формулам:

L   ^L U = 1 ^X ou ^y u. К __ Е и = 1 ^X iu ^y u.

^ь0 =       • ^{b ii} = aK XS ’

N г2

• 7   _ L u = 1 ^X ju ^y u

• ^jj    N™ (y 2 V

^Lu = 1 l ^X/u )

и будут связаны коррелированно между собой, так как

• ^LN =1 X 0u X 2u ^ 0 и ^LN =1 X 2uX/u ^ 0,  (9)

где  х0м=1,0  безразмерная величина факторов [2].

Рассмотренная задача - линейного программирования, решение которой определяет удельный вес участия каждого вида сырья в производстве единицы искомого продукта при обеспечении минимальной стоимости его выработки. Решение данных систем уравнений осуществляется при использовании пакетов программ по оптимизации рецептур пищевых продуктов, позволяющих в результате их математической обработки определить относительное содержание сырьевых компонентов, а также величину энергетической ценности проектируемых композиций. Результаты расчёта сведены в табл. 2.

Таблица 2 - Пищевая и энергетическая ценность сырного продукта с растительным наполнителем

Составляющие	Норма потребления, г (мг. ккал)/сут	Контрольный плавленый сыр		Опытный плавленый сыр
		Содержание	Удовлетворение суточной потребности, %	Содержание	Удовлетворение суточной потребности, %
Белки, г/100 г	77,5	11,3	14,5	29,75	38,63
Жиры, г/100 г	87	10,9	12,5	18	20,1
Каротиноиды, мг/100 г	1,5	0,27	18,0	0,54	36
Витамин     С, мг/100 г	75	1,08	1,4	2,40	3,2

В таблице 2 отражены значения удовлетворения суточной потребности человека в витаминах, жирах, белках. Из этого следует, что разработанный по полученной математической модели плавленый сыр удовлетворяет потребности человека лучше, чем контрольный образец. Трехмерное представление указанной математической модели, полученной с использованием пакета программ Matlab, показано на рис.1. Близкие к ним зависимости оказались и при использовании электронного процессора MS Excel. Имеющееся небольшое расхождение, очевидно, связано с тем, что, как показала практика многочисленных вариантов использования программ Matlab, решение уравнений, начиная с третьей и более степени, дает ощутимые погрешности [3].

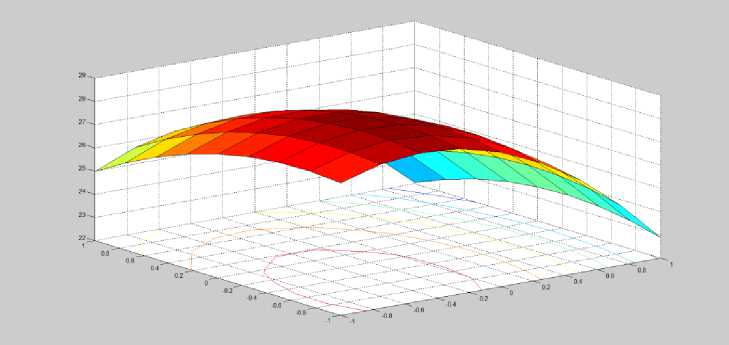
Рис.1 - Представление математической модели, отражающей зависимости свойств плавленого сыра от состава ингредиентов.

Полученный продукт подтверждает возможность корректирования качественных показателей от его состава.

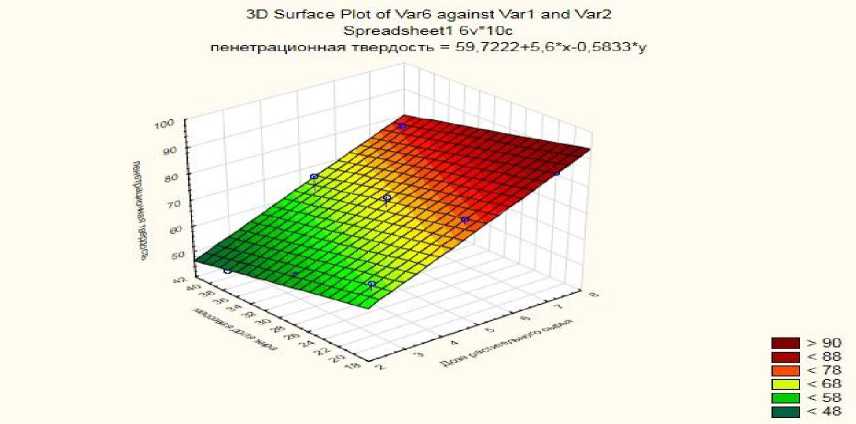
Рис. 2 - Зависимость пенетрационной твердости плавленого сыра от дозы вносимого растительного сырья и массовой доли жира.

Варьируя дозу вносимых компонентов и их свойства, можно корректировать консистенцию пищевого продукта. Данное предположение подтверждает рис. 2, на котором показана зависимость пенетрационной твердости от дозы вносимого растительного сырья и массовой доли жира. Как видно из рисунка, зависимость линейная, что говорит о прямой зависимости твердости сыра от дозы вносимого растительного сырья.

Заключение

С помощью разработанного алгоритма и математической модели определена оптимальная рецептура выработанного плавленого сыра. Плавленый сыр получил высокие баллы по органолептическому анализу.

По результатам обработки экспериментальных данных с использованием методов математической статистики и компьютерных средств выявлено, что математическая модель адекватна, а выполненный по предложенной рецептуре плавленый сыр удовлетворяет суточной потребности человека лучше, чем контрольный образец.

Предложенная рецептура удовлетворяет заявленной функциональной направленности по улучшению качества исследуемого сырного продукта: в нем содержание холестерина по сравнению с контрольным плавленым сыром - уменьшилось на 75%; содержа- ние пищевых волокон - повысилось на 20%. Кроме того, употребление 100 г сырного продукта обеспечивает суточную потребность человека в полиненасыщенных жирных кислотах на 29%.