Математическое моделирование спектрально-корреляционных, статистических и электродинамических характеристик физико-технических систем

Повышение уровня фундаментальной математической и физико-технической подготовки актуально в связи с существенным повышением требований к подготовке молодых специалистов по современным телекоммуникационным и геоинформационным технологиям со стороны работодателей. Студенты 1-2 курсов достаточно уверенно владеют основами компьютерных и телекоммуникационных технологий благодаря массовому внедрению сотовой связи и Интернета. Однако одновременно с этим следует отметить снижение общей математической и физической «культуры мышления» основной массы студентов, истоки которой закладываются и формируются еще в начальной школе. В высшей школе существует серьезное противоречие между математической и физико-технической подготовкой студентов. Причина этого явления заключается в отсутствии тесных связей между учебными курсами, а также в том, что, как правило, преподаватели кафедр математического цикла глубоко не вовлечены в научную работу современного физико-технического уровня из-за большой загруженности учебной работой.

Цель статьи - показать связь и внутреннее единство математического и физикотехнического подходов при компьютерном моделировании электромагнитных процессов в линейных и нелинейных системах на примере двухсеместрового лабораторного практикума . В статье развивается подход к определению «оптимальной» структуры лабораторных работ, описаны соответствующие математические (цифровые) модели и результаты их практиче- ского применения по дисциплинам «Теория передачи сигналов» и «Основы геоэлектромагнетизма» для студентов физико-технических и телекоммуникационных специальностей Бурятского государственного университета и Иркутского государственного университета путей сообщения. Следует отметить, что профессиональная научная деятельность авторов доклада связана с Сибирским отделением РАН. Преподавание в ВУЗе позволяет нам отчетливо увидеть достоинства и недостатки в подготовке молодых специалистов, дать им правильную практическую оценку и тем самым повысить эффективность обучения.

В нашем подходе учебный курс рассматривается как множество элементов знаний (наиболее значимых математических и физическо-технических понятий, свойств, утверждений, законов и правил). Под типовым лабораторным заданием нами понимается задание, которое направлено на выполнение и проверку некоторого подмножества элементов знаний за академическое занятие. Структурой лабораторного занятия будем называть набор типовых заданий, включенных в конкретную лабораторную работу, а оптимальной структурой – набор заданий, который позволяет студенту понять сущность физических процессов и явлений и их математическое описание адекватной моделью, а преподавателю – сделать объективный вывод о степени усвоения рассматриваемой темы, удовлетворяющей определенному критерию. Лабораторный практикум включает необходимые и традиционно сложившиеся темы (810 тем) по теории сигналов и электродинамике. Он базируется на пакете программ «Редактирование и обработка сигналов»[1,2] и программном комплексе «Импеданс» [3,4]. Перечень работ по разделам курса высшей математики:

• 1.    « Ряды и интеграл Фурье. Корреляционный анализ»

• -    Исследование спектров сигналов.

• -    Гармонический синтез и анализ периодических сигналов.

• -    Корреляционный анализ детерминированных сигналов.

• -    Исследование сигналов с линейной частотной модуляцией (ЛЧМ).

• 2.    «Теория вероятностей и математическая статистика»

• -    Исследование законов распределения случайных сигналов.

• -    Прохождение случайных сигналов через линейные и нелинейные цепи.

• -    Исследование корреляционных функций и энергетических спектров случайных процессов.

• 3.    «Интерполяция функций»

• - Дискретизация непрерывных сигналов во времени (теорема Котельникова).

• 4.    «Прямые и обратные задачи»

• -    Интерпретация радиоимпедансных зондирований методом подбора.

• -    Интерпретация радиоимпедансных зондирований методом регуляризации А.Н.Тихонова.

• 1.    Спектрально-корреляционные и статистические характеристики сигналов

Пособия [1,2] содержат описания и порядок выполнения лабораторных работ. Для удобства приведены методические рекомендации по использованию пакета программ EDSW. Разработанный лабораторный практикум с использованием пакета программ «Редактирование и обработка сигналов» позволяет применять любую операционную среду, начиная с Windows-95. Программа моделирует лабораторный стенд с полем для графиков исследуемых сигналов и необходимым набором контрольно-измерительной аппаратуры. Общий вид главного меню программы EDSW представлен на рис. 1.

Рис.1. Главное меню программы EDSW

«Генератор сигналов» формирует тестовые сигналы с хорошо известными математическими моделями, например:

1) гармонический сигнал 5 ( t ) = A q cos ( sinУа + ф\cot + ф н ) ,

2) периодическая последовательность прямоугольных импульсов с амплитудой U , длительностью т и периодом повторения T s ( t ) = s ( t ± nT ) ;

3) гауссовский шум – случайный процесс с плотностью вероятности распределения амплитуд

¹ — u ( 2 ст )        — 2

p(u) = .— e         , где ст - дисперсия, ст - СКО (рис.2).

V 2 пст

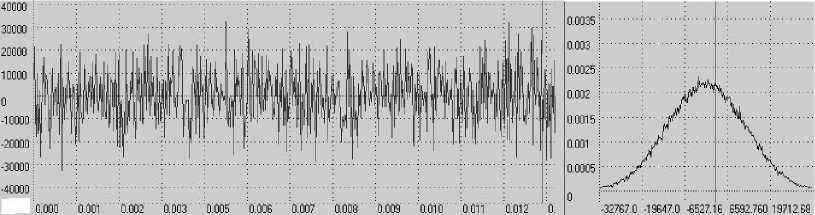
Рис.2. Гауссовский шум и плотность вероятности распределения амплитуд

В качестве примера рассмотрим тему «Ряды и интеграл Фурье», которая раскрывается в лабораторной работе «Исследование спектров сигналов. Гармонический синтез сигналов». Цель работы – развить у студентов спектрально-временное представление в системе «амплитуда–частота» (спектроанализатор) и. «амплитуда–время» (осциллограф). Здесь главное – показать, что периодические сигналы полностью описываются рядом Фурье по гармоникам основной частоты f = 1/ T , где T - период повторения. А непериодические (однократные) сигналы представляются интегралом Фурье. Так, для импульсный периодической последовательности униполярных импульсов с амплитудой U = 30000 у.е., т = 1 мсек, T = 5 мсек, получаем дискретный (линейчатый) спектр с гармониками на частотах 200, 400, 600, 800, 1200 Гц, „., а частота 1000 Гц «зануляется», т. к. при скважности T/т = 5 пятая, 10-ая, 15-ая и другие кратные 5 гармоники равны 0 (рис.3).

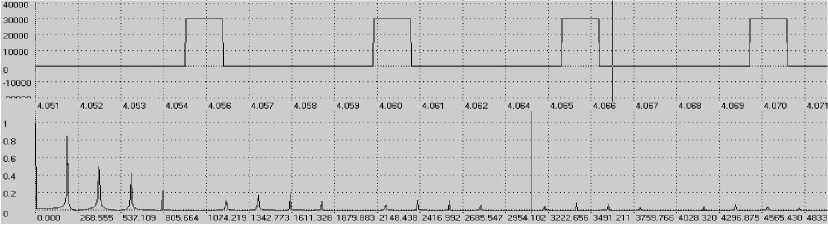
Рис.3. Импульсная периодическая последовательность и амплитудно-частотный спектр

При увеличении периода повторения T (стремлении T к бесконечности, например, взяв T = 1 сек) получаем сплошной спектр, описываемый функцией «координатный синус» Sincx = ( Sinx )/ x (рис.4). Здесь первый нуль находится на частоте 1000 Гц = 1/ т , второй нуль - 2000 Гц = 2/ т и т.д.

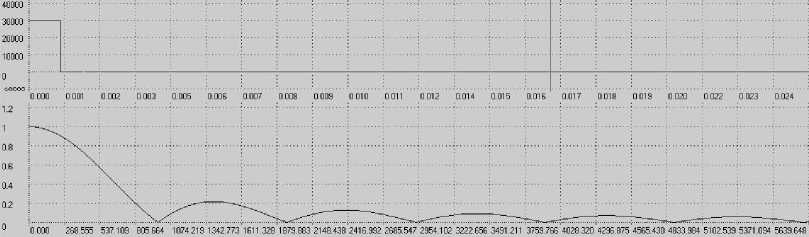
Рис. 4. Импульсная последовательность ( T ^ да ) и амплитудно-частотный спектр Теперь рассмотрим гармонический синтез сигналов. Пусть необходимо синтезировать пилообразное напряжение:

S ( t ) = 2 A 0 ( sin Q t - 1/2 sin 2 Q t + 1/3 sin 3 Q t - 1/4 sin 4 Q t + 1/5 sin 5 Q t - 1/6 sin 6 Q t +.. ). Зададим 2 A 0 = 10000 = 10000 у.е., Q = 200, 400, 600 Гц и т.д. В результате суммирования гармонических колебаний с кратными частотами получаем периодический сигнал, аппроксимирующий пилообразное напряжение. Его спектр показывает пять использованных при синтезе гармоник, амплитуды которых убывают обратно пропорционально номеру гармоники (рис.5).

Описания лабораторных работ в методических пособиях [1,2] включают краткую теорию, цель работы, лабораторное задание, программу работ, требования к оформлению отчета и контрольные вопросы.

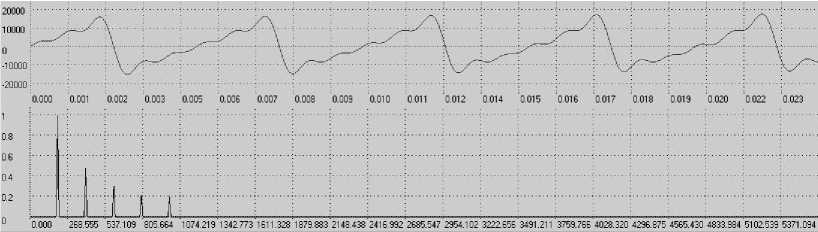
Рис.5. Пилообразное напряжение и его амплитудно-частотный спектр

2 . Прямые и обратные задачи радиоимпедансного зондирования

В лаборатории геоэлектромагнетизма Отдела физических проблем при Президиуме Бурятского научного центра СО РАН развита теория, разработаны численные методы и создано программное обеспечение решения прямых и обратных задач радиоимпедансного зондирования для вертикально-неоднородных (дискретно-слоистых и градиентных) сред с учетом эффектов частотной дисперсии основных электрических параметров земной коры.

Создан пакет прикладных программ «Импеданс» [3]. Он предназначен для решения прямой и обратной задач распространения электромагнитной волны в слоистой среде:

1) расчет поверхностного импеданса по известному геоэлектрическому разрезу;

Методика расчетов прямой задачи основана на понятии приведенного поверхностного импеданса плоской волны на поверхности горизонтально-слоистой структуры, с помощью которого можно учесть влияние подстилающей среды на распространение радиоволн:

8 = Er (HH,Z о), где ET,HT - горизонтальные взаимно перпендикулярные компоненты электрического и магнитного полей на границе раздела «воздух-земля»; Zо = Дц /^о = 377 Ом - характеристический импеданс свободного пространства.

Для решения обратной задачи электромагнитного зондирования для слоистой полупроводящей среды, удовлетворяющей импедансным граничным условиям, разработан алгоритм метода регуляризации на основе гипотетического разреза. Сглаживающий функционал L ₂

А.Н. Тихонова имеет вид: Ma [g] = I[g] + aQ[g], где I[g] = E 8/ — 8/   - функционал не- l=1          3

вязки;

N

^ [ g ] = E P n ^s n

—

^ n

n = 1

2 N

+ E q n ^ n = 1

n ^u n

2 N — 1

⁺ E ^rn h n ^— h n = 1

⁰ n

– стабилизирующий функционал;

g = ( e . o .h ) - параметры многослойной полупроводящей среды; a - параметр регуляризации; ( f ⁰ , ^ ⁰ ,h ⁰ ) - гипотетическое распределение параметров разреза; p_n,q_n,r_n - веса соответствующих параметров; 8 / - экспериментальные значения импеданса на / -ой частоте.

Минимизация рассматриваемого функционала производилась с помощью метода Ньютона-Канторовича (метода линеаризации). Осуществляя линеаризацию оператора прямой задачи A в окрестности имеющегося приближения g ^{H n} ) , получили формулу:

Д д = ( B T B + a l ) ^{— 1} • ( B T д ₃ + a Ig ⁰ ), где B - матрица Якоби для A с элементами B ij = ( с А / d g j ) g = g n . Для решения системы линейных уравнений на каждом шаге итерационного процесса использовался метод псевдообращения. С использованием сингулярного разложения B ( gⁿ ) = U Л V T получена окончательная формула для решения:

Д g = VЛ ( Л ² + a l _r) ^{— 1} U ^T д ₃ + ( VЛ ² V ^T + a l _r) ^{— 1} a g ⁰ .

Критерием выбора «наилучшего» геоэлектрического разреза служит минимум среднеквадратического отклонения экспериментальных значений импеданса от рассчитанных для модели n -слойной среды.

Программы пакета созданы с помощью объектно-ориентированного языка программирования Visual Basic for Applications и функционируют в среде Excel. Дружественный графический интерфейс с системой меню облегчает работу пользователям с различным уровнем компьютерной подготовки. Поэтапно осуществляется ввод, просмотр, обработка измеренных данных, вывод результатов в наглядной форме в виде таблиц и диаграмм, сохранение результатов в файлы. Интерактивный режим позволяет контролировать процесс интерпретации на каждом этапе работы. При этом существенно снижается погрешность интерпретации и повышается надежность получаемых результатов. Все программы прошли тестирование, апробированы на модельных примерах. Проведена оценка погрешности определения параметров геоэлектрического разреза. Кроме указанных выше программ, пользователю предоставлены также следующие возможности:

• —    статистические расчеты импеданса в заданном диапазоне частот или получение статистических оценок модуля и фазы поверхностного импеданса однородной в геологическом отношении области (комплекса горных пород);

• —    учет частотной дисперсии электрических параметров среды;

• -    расчеты для градиентных полупроводящих сред путем аппроксимации большим числом плоскопараллельных однородных слоев с электрическими параметрами, соответствующими профилю неоднородного слоя (кусочно-градиентная модель наилучшим образом отражает реальное строение многолетнемерзлого грунта);

• -    получение пространственного распределения параметров геоэлектрического разреза при радиоимпедансном зондировании при площадной съемке или на профиле.

В лабораторном практикуме для студентов предложены различные модели природных слоистых сред типа «лед-соленая (морская) вода», «лед-пресная вода», «лес на горном хребте» и другие. Особый интерес представляет «вечная мерзлота», занимающая около 25% площади суши Земного шара. Одной из особенностей мерзлых пород является наличие значительной частотной дисперсии электрических свойств малопроводящих мерзлых рыхлых отложений. Слоистые геоэлектрические структуры, встречающиеся на мерзлоте, дают сильный эффект осцилляции модуля δ и фазы ϕ δ импеданса в индуктивной и емкостной областях (рис. 6). Учет частотной дисперсии электрических свойств мерзлых рыхлых отложений приводит к почти монотонной частотной зависимости импеданса. На рис.6 принято, что в диапазоне частот 10² ÷ 10⁶ Гц сопротивление ρ ₂ геоэлектрического разреза (ГЭР) изменяется по формуле lg ρ ₂ = 4 , 8 - 0 , 166 lg f .

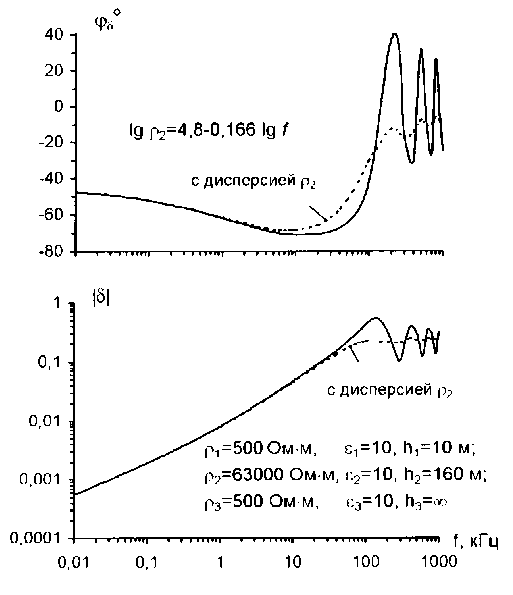
Рис. 6. Осцилляции модуля и фазы импеданса для модели мерзлоты.

Предложенный регуляризирующий алгоритм продемонстрировал свою эффективность в процессе обработки и анализа экспериментальных данных и позволяет восстанавливать структуру достаточно сложных геоэлектрических разрезов. Были проинтерпретированы результаты зондирований в диапазоне 17-529 кГц в 23 типичных пунктах, характеризующих мерзлые осадочные и кристаллические породы, а также акваторию реки Колыма и тундровые озера (р-н п. Черский). Установлено, что электрическое сопротивление рыхлых мерзлых пород во много раз меньше известных по ВЭЗ значений, а зоны с аномально низким сопротивлением (10-60 Ом.м) имеют большое территориальное распространение. Полученные результаты важны при прогнозировании параметров ГЭР криолитозоны.

Создана программа графической интерпретации радиоимпедансных зондирований [4], предназначенная для определения параметров (1 ^ 4)-слойного геоэлектрического разреза (диэлектрических проницаемостей, удельных сопротивлений и толщин слоев) по частотной зависимости поверхностного импеданса. В ней реализован графический вариант метода подбора. Искомые параметры разреза выбираются из критерия наилучшего совмещения теоретических кривых и экспериментальных значений импеданса. Достоинства: интерактивный режим, наглядность, быстрота обработки. Программа позволяет выбрать модель среды, выявить эквивалентные разрезы, получить начальные параметры разреза, которые затем можно уточнить методом регуляризации. На рис. 7 представлен вид рабочего окна программы для 3-слойного разреза.

В целом лабораторные работы проводились с интересом, хорошей адаптацией и усвоением изучаемого материала. Разработанный цифровой программный комплекс характеризуется многофункциональностью и универсальностью.

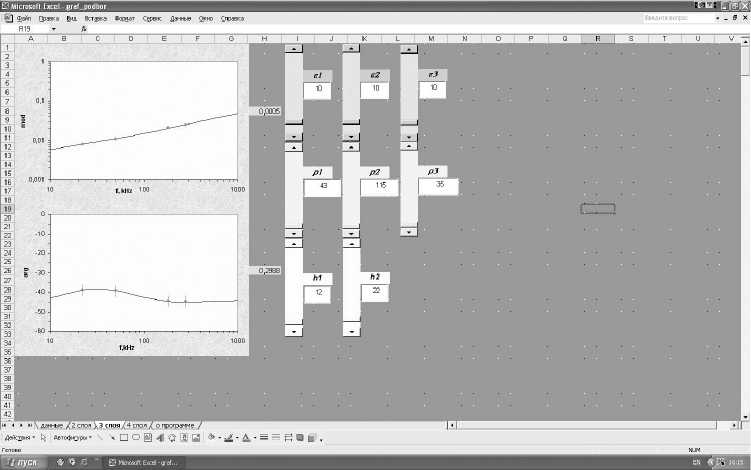
Рис. 7. Вид рабочего окна программы графической интерпретации данных радиоимпедансных зондирований для 3-слойного разреза.

Заключение

Разработан комплекс лабораторных работ для моделирования спектральнокорреляционных, статистических и электродинамических характеристик физикотехнических систем, имеющий широкие функциональные возможности. Цифровой программный комплекс может быть использован при УИРС, выполнении курсовых, дипломных работ и проектов.

Комплекс может быть полезен при изучении курсов «Основы радиоэлектроники», «Статистическая радиофизика», «Радиотехнические цепи и сигналы». В связи с развитием и использованием дистанционного образования открываются новые направления в применении данного электронного программно-методического лабораторного практикума как в целях обучения, так и переподготовки кадров в различных учебных заведениях Восточной Сибири.