Математическое моделирование течений многокомпонентных сред в кольцевых соплах
Автор: Карташев Александр Леонидович, Карташева Марина Анатольевна
Рубрика: Расчет и конструирование
Статья в выпуске: 2 т.13, 2013 года.
Бесплатный доступ
Рассмотрены течения многокомпонентных сред в кольцевых соплах управляемых газоструйных систем различных геометрических конфигураций на различных режимах работы. Предложен подход для моделирования течений многокомпонентных сред в кольцевых соплах со сложной ударно-волновой структурой. Получены результаты численных исследований динамики многокомпонентных сред в кольцевых соплах.
Кольцевое сопло, управляемая газоструйная система, математическое моделирование, многокомпонентная среда
Короткий адрес: https://sciup.org/147151635
IDR: 147151635
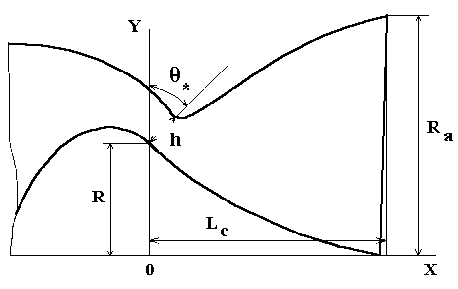
Список литературы Математическое моделирование течений многокомпонентных сред в кольцевых соплах
- Карташев, А.Л. Математическое моделирование течений в кольцевых соплах: моногр./А.Л. Карташев, М.А. Карташева. -Челябинск: Издат. центр ЮУрГУ, 2011. -158 с.
- Карташев, А.Л. Математическое моделирование двухфазных течений в кольцевых соплах/А.Л. Карташев, Б.М. Тюлькин//Ракетно-космическая техника. Серия XIV. -2001. -Вып. 2 (47). -С. 51-59.
- Карташев, А.Л. Исследование особенностей движения многофазных сред в кольцевых соплах/А.Л. Карташев//Тезисы Международной конференции «VI Забабахинские научные чтения», 24-28 сент. 2001 г. -Снежинск, 2001. -С. 30-31.
- Газовая динамика двухфазных течений в соплах/И.М. Васенин, В.А. Архипов, В.Г. Бутов и др. -Томск: Изд-во Томского ун-та, 1986. -262 с.
- Двухфазные моно-и полидисперсные течения газа с частицами/Л.Е. Стернин, Б.Н. Маслов, А. А. Шрайбер и др. -М.: Машиностроение, 1980. -176 с.
- Вилюнов, В.Н. Моделирование двухфазного течения смеси газа с горящими частицами металла в полузамкнутом канале/В.Н. Вилюнов, А.Б. Ворожцов, Ю.В. Фещенко//Физика горения и взрыва. -1989. -Т. 24, № 3. -С. 39-43.
- Архипов, В.А. Эффекты динамического взаимодействия конденсированных частиц в камере сгорания РДТТ/В.А. Архипов, А.С. Ткаченко, В.Ф. Трофимов//Физика горения и взрыва. -1999. -Т. 35, № 2. -С. 41-46.
- Сарнер, С. Химия ракетных топлив/С. Сарнер. -М.: Мир, 1969. -488 с.
- Рычков, А.Д. Математическое моделирование газодинамических процессов в каналах и соплах/А.Д. Рычков. -Новосибирск: Наука, 1988. -224 с.
Статья научная
