Математическое моделирование течения сплошных сред в вихревой камере

Цитирование: Зырянов А. В. Математическое моделирование течения сплошных сред в вихревой камере / А. В. Зырянов, В. Д. Сарычев, В. И. Мурко, В. И. Карпенок // Журн. Сиб. федер. ун-та. Техника и технологии, 2024, 17(8). С. 1090–1099. EDN: KGVYOU онных топлив. При использовании данной технологии для сжигания ВУТ имеются проблемы, сдерживающие ее практическое применение. В первую очередь это недостаточность теоретических данных по оценке влияния основных характеристик ВУТ (выхода летучих веществ, влажности, зольности и, соответственно, низшей теплоты сгорания топлива) на процессы воспламенения и горения, отсутствие научно обоснованных методических рекомендаций по выбору конструктивных параметров вихревых адиабатических топок (внутренние размеры и диаметр пережимного окна) для надежного сжигания топлива в зависимости от теплопроизводительно-сти теплогенераторов малой и средней мощности, в том числе при переводе мазутных, газовых и угольных котлов со слоевыми топками на сжигание ВУТ [5–11]. Опубликовано много работ, в которых приводятся результаты расчетов физико-химических процессов на фоне сложных турбулентных гидродинамических течений [12–19].

Численное моделирование течения газа и горения частиц в вихревой камере проводилось в работах [20–23]. В расчетах использовались инжекторы сжатого воздуха и топлива, расположенные на уровне нижних воздухозаборников. Геометрически воздухозаборники и топливные инжекторы расположены попарно на противоположных вершинах вписанного прямоугольника. Расчет газодинамических процессов в камере выполнялся с помощью программы STAR-CCM+ (версия 6.02), разработанной CD-adapco.

Для описания газового потока использовались модели Эйлера. Симуляция частиц топлива проводилась по лагранжевой фазе. В расчетах использованы нестационарные численные модели на основе осреднения по Рейнольдсу (RANS). Применялась k-ε турбулентная модель. Задача решалась в трехмерной постановке. Для численных расчетов использовался метод конечных объемов. В результате расчетов показано, что в середине камеры формируется осевой поток вдоль вертикальной оси, что обусловлено разницей давлений на выходе. Конфигурация потоков от сопел сохраняется в данном сечении, а под сводом камеры образуются области повышенных скоростей. Предполагается, что наличие последовательных тороидальных вихрей увеличивает время пребывания частиц топлива в зоне реакции. Согласно приведенным данным, поток в вихревой камере можно разделить на две зоны. В первой зоне (0 < r < R) поток аналогичен потоку Куэтта-Пуазейля с вращающимся цилиндром, имеющим угловую скорость Ω, радиус R и средний перепад давления в верхней и нижней частях цилиндрической камеры. Во второй зоне, прилегающей к краю цилиндра, формируется сложный поток из-за взаимодействия двух струй и пограничных слоев. Таким образом, выявлен сложный характер течения в вихревой камере с тангенциальным вдувом, что требует продолжения исследований газодинамического течения как основы для дальнейшего установления влияния процессов горения на структуру потоков. С учетом того, что в пакете STAR-CCM используется метод конечных объемов, а в пакете COMSOL Multiphysics метод конечных элементов, выбор параметров расчета искусственной вязкости для получения устойчивого решения нельзя переносить автоматически. Кроме того, лицензия STAR-CCM действует ограниченное время, а лицензия COMSOL Multiphysics бессрочная.

Поэтому целью исследования явилось создание проекта в COMSOL Multiphysics течения сплошной среды в вихревой камере. При этом задавались параметры среды и геометрические характеристики вихревой камеры, включая плотность, вязкость, скорости потоков и температуру. Граничные условия на стенках камеры и параметры потоков на входе и вы-– 1092 – ходе устанавливались для обеспечения корректного математического описания процессов. Был выбран и реализован оптимальный численный метод, обеспечивающий стабильность и точность решений.

Математическая постановка задачи

В расчетах применялись нестационарные, осредненные по Рейнольдсу уравнения Навье-Стокса с k – ε моделью турбулентности для идеального газа. Такие уравнения использовались для моделирования различных трехмерных газодинамических течений в многих работах. В декартовой системе координат нестационарное течение вязкого сжимаемого газа относительно фильтрованных переменных описывается системой уравнений в дивергентном виде:

St dx_t 5т, йг₃

Система (1) дополняется уравнением состояния идеального газа:

P = (У~ l)p(^{e _} 0, 5(ip + ip + ii^)).

Компоненты векторов системы (1) определяются по формулам:

R =

P

Pi'i pu2 P"i , PC ,

; Pt =

m

Ph-'1 ЛУ

тр = P"i"j + S^p, h = e + p/ p

Компоненты тензора вязких напряжений и координаты вектора теплового потока находятся из соотношений:

—— 4-------— 3.. dx. dxf 3 dxk где t – время, с; ρ – плотность, кг/м3; u1, u2, u3 – компоненты вектора скорости в направлениях x1, x2, x3, м/с; p – давление, Па; γ – отношение удельных теплоемкостей; μ – эффективные значения вязкости и теплопроводности, Па∙с, Вт/(К∙м).

Уравнения (1) формально совпадают с уравнениями Навье-Стокса с эффективными вязкостью и теплопроводностью, вычисляемым по формуле:

μ = μ m + μ t ,

где c p – теплоемкость при постоянном давлении, Дж/кг∙К; μ t – турбулентная вязкость, Па·с; Pr = 0,72; Pr _t = 0,8 – числа Прандтля для воздуха.

Рейнольдсовы напряжения выражаются через скорости деформации, выраженные через фильтрованные скорости:

dp du.

dn.

4 =-Р'Ш = P, —^L +—^{L __}R/—^L + PM^-

Система уравнений (1–7) – является осредненными по Рейнольдсу уравнениями Навье-Стокса (RANS). Эту систему уравнений обычно дополняют моделью эмпирической турбулентности

В стандартной k – ε модели используются уравнения переноса турбулентной кинетической энергии k и диссипации энергии ε :

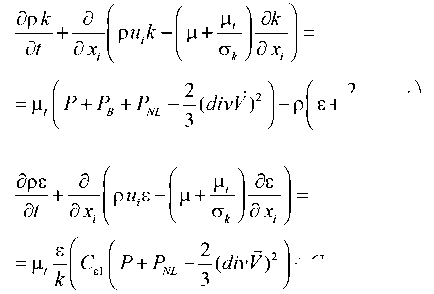
где р дщ

Для нахождения турбулентной вязкости используется формула:

cuPk2

Hr = A----- где fμ – эмпирическая функция. Константы модели имеют следующие значения:

CM = 0,09; c81 = 1,44; ce2 = 1,92; ст, = 1,0; стЕ =1,3.

Таким образом, задача (1–12) является полностью замкнутой, то есть число уравнений совпадает с числом неизвестных функций.

Результаты расчетов

Была создана трёхмерная модель вихревой камеры в COMSOL Multiphysics. Геометрия включает цилиндрическую камеру с входным и выходным отверстиями. Патрубки с входными отверстиями расположены тангенциально на боковой стенке камеры. Патрубок с выходным отверстием расположен на торцевой верхней поверхности камеры (рис. 1).

Для всей области модели была построена сетка, использующая тетраэдрические элементы, с учётом особенностей геометрии и областей с высокими градиентами (рис. 2).

В качестве физической модели был выбран интерфейс Turbulent Flow, k-ε для описания турбулентного потока внутри камеры. На входе камеры задаётся граничное условие Inlet с определённой скоростью потока. На выходе камеры установлено условие Outlet с нулевым давлением. Для стенок камеры использовано условие Wall с параметром No Slip, чтобы смоделировать торможение потока на границах.

Для вычисления устойчивого состояния потока в вихревой камере был использован Stationary решатель. Решение было получено после корректировки начальных условий и параметров расчета, обеспечивающих устойчивость процесса.

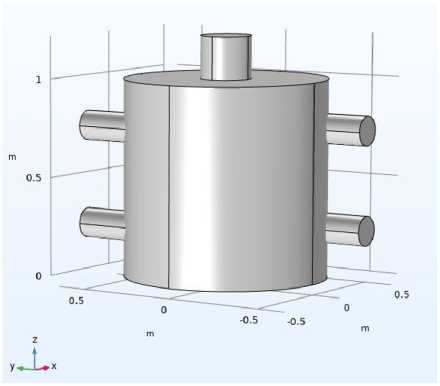
Рис. 1. Геометрия вихревой камеры

• Fig. 1.    Geometry of the vortex chamber

  

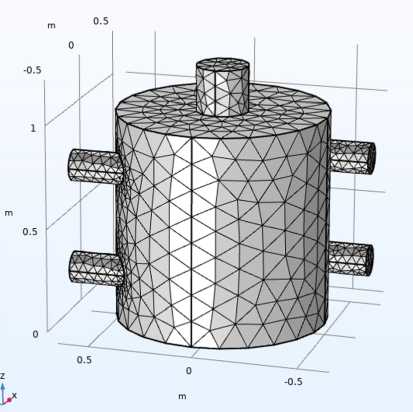
Рис. 2. Сетка вихревой камеры

• Fig. 2.    Mesh of the vortex chamber

Для анализа течения были построены Streamlines (линии тока), которые визуализируют траектории частиц внутри камеры (рис. 3).

Также был построен график Velocity Magnitude на сечении z=const, показывающий распределение скоростей в вихревой камере (рис. 4).

Дополнительно создан Velocity Slice по тому же сечению z, чтобы получить визуализацию слоя скорости и увидеть более детальную структуру потока (рис. 5).

Surface: Velocity magnitude (m/s) Line: Velocity magnitude (m/s) Streamline: Velocity field

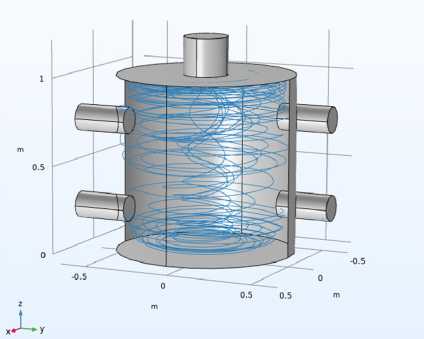
Рис. 3. Линии тока внутри камеры

Fig. 3. Streamlines inside the chamber

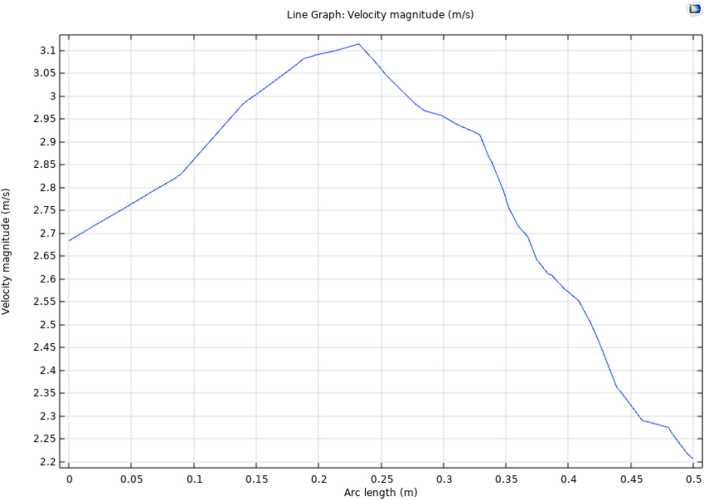
Рис. 4. График распределения скоростей в вихревой камере

Fig. 4. Velocity distribution plot in the vortex chamber

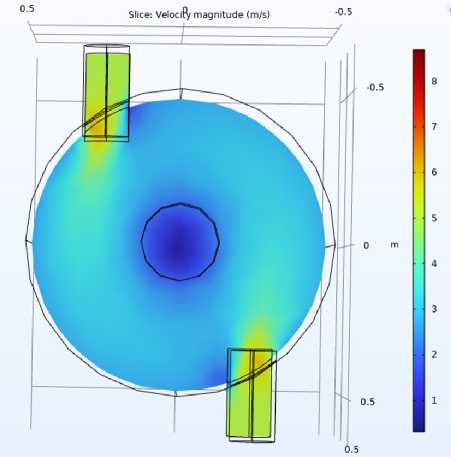
Рис. 5. Визуализация слоя скорости

Fig. 5. Velocity layer visualization

Заключение

Проведенные численные расчеты и моделирование подтвердили работоспособность и эффективность предложенной модели вихревой камеры для сжигания ВУТ. В рамках исследования была построена трехмерная модель камеры с использованием интерфейса Turbulent Flow k-ε, позволившая качественно описать динамику турбулентного потока внутри камеры.

Моделирование в программном комплексе COMSOL Multiphysics позволило задать детализированную расчетную сетку, адаптированную к геометрическим особенностям камеры, и использовать методы, оптимально подходящие для задач такого типа. Турбулентная модель k–ε, примененная в данном исследовании, продемонстрировала высокую точность предсказания газодинамических характеристик, включая распределение осевой скорости и вихревых структур, подтверждая ее применимость для высокоскоростных, турбулентных течений.

Таким образом, разработанная модель вихревой камеры для сжигания ВУТ представляет собой надежный инструмент для анализа и проектирования энергоэффективных установок.