Математическое моделирование теплои массообменных процессов в реакторе анаэробного сбраживания

Разработанная технология утилизации (переработки) отходов путем анаэробного сбраживания строится на базе муниципальных образований, жилищно-коммунального сектора и других источников их образования.

Она предназначена для переработки пищевых отходов в местах их образования с целью:

• - предотвращения экологического ущер -ба, наносимого окружающей среде от полигонов ТБО;

• -    получения энергетических ресурсов (биогаз, электрическая и тепловая энергия);

• -    получения экологически чистых органических удобрений;

• -    предотвращения платежей за образование отходов.

Технологические установки микробиологической утилизации органических отходов (коммунальные и пищевые отходы, а также отходы пищевых и кормовых производств) позволяют в качестве конечных продуктов получать биогаз с большим содержанием метана и органические, азотосодержащие удобрения.

Таким образом, существенно уменьшается загрязнение окружающей среды отходами:

• -    жилищно-коммунального сектора;

• -    сельского хозяйства (животноводство, растениеводство);

• -    пищевой и кормовой промышленности (мясокомбинаты, спиртзаводы, сыроваренные заводы, молокозаводы, маслоэкстракционные предприятия и пр.)

Чернецкая А.А., Смолко Ю.Н., 2013

Предлагаемый способ сбора и утилизации (переработки) пищевых отходов методом анаэробного сбраживания базируется на адаптации сырьевых комплексов к технологическим условиям переработки анаэробными бактериями, при этом подбор рецептур и технологических параметров обеспечивает наибольшую эффективность процесса биосинтеза.

Главным преимуществом разработанной технологии является возможность утилизации пищевых отходов сложного морфологического и непостоянного состава, а также получение на выходе экологически безопасных продуктов . При этом резко снижаются выбросы вредных веществ в окружающую среду.

Исследуемый процесс анаэробного сбраживания органического сырья является многофакторным. Биомасса, в конечном итоге, представляет собой три фазы: твердая фаза, суспензия и водно-масляная эмульсия, а так же зоны перехода.

Математическая модель тепло- и массо-обм енных процессов в реакторе анаэробного сбраживания должна отвечать следующим условиям:

• -    строиться с учетом трехслойной структуры среды в реакторе (массообменный процесс);

• -    учитывать различия газовыделений в трех слоях биомассы (массообменный процесс);

• -    строиться с учетом зависимости теплофизических характеристик слоев от состава питающей смеси (массообменный процесс);

• -    учитывать гидродинамические характеристики течения реакционной массы в зависимости от интенсивности перемешивания;

• -    учитывать характер консорциума;

• -    относиться к разнородности реакционной массы;

• -    реализовывать учет зависимости характеристики потока жидкости в реакционном пространстве от интенсивности перемешивания;

• -    протекать при давлении над поверхностью реакционного пространства, не превышающем 0,02 атм.

Рассматривается реактор с рубашкой и мешалкой, внутри которого осуществляется процесс анаэробного сбраживания органической массы (рисунок 1).

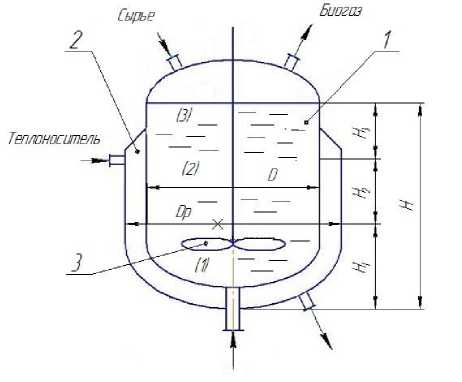
Рисунок 1- Реактор для получения биогаза:

1 - корпус реактора, 2 - рубашка, 3 - мешалка.

Водный раствор органической массы периодически загружается в реактор с одновременным отводом продуктов разложения. Образующийся биогаз отводится через верхний штуцер. Рабочая среда при работе биогазового реактора расслаивается на три области:

• -    суспензия, состоящая из твердых частиц органической природы, взвешенных в слое воды;

• -    светлый слой, состоящий, преимущественно, из воды;

• -    масляный слой.

После первоначальной загрузки реакционная среда нагревается теплоносителем, циркулирующим в рубашке, до температуры 37 оС. При такой температуре процесс анаэробного сбраживания протекает наиболее интенсивно. В результате жизнедеятельности бактерий вырабатывается биогаз, состоящий на 70 % из метана и примерно на 30 % из углекислого газа с теплотой сгорания примерно 25-

• 29 МДж/нм³. Производительность биореактора при оптимальном режиме составляет 2-7 м³/сутки на 1 м³ реакционной смеси.

Эффективность работы биореактора определяется многими параметрами [1], важнейшими из которых являются температура, интенсивность перемешивания, показатель рН и др.

Субстрат подается в реактор в непрерывном режиме или мелкими порциями, а прореагировавшее сырье выводится из реактора.

Газовые пузыри зарождаются, преимущественно, в нижней части реактора на поверхности твердых органических частиц субстрата и стенках. При достижении радиуса отрыва Ко газовый пузырь отрывается от твердой поверхности и всплывает. По мере движения его радиус увеличивается из-за массообмена с жидкой фазой. Закон изменения радиуса пузыря и скорость всплытия существенно влияют на процессы тепломассообмена и производительность реактора.

На первом этапе происходит зарождение, отрыв и всплытие газового пузыря.

Радиус пузыря, при котором происходит его отрыв от твердой поверхности, определяется соотношением [2]:

R o = 0,016 /—^— , (1)

• -^ ЩР ж -Р г )

где 6 - краевой угол в момент отрыва; а - коэффициент поверхностного натяжения жидкости; рж, рг- плотности жидкости и газа.

После отрыва газовый пузырь всплывает. В процессе всплытия количество газа в нем увеличивается пропорционально коэффициенту массоотдачи и площади поверхности газового пузыря.

Закон изменения объема газового пузыря определяется соотношением:

р г — = -^—PPrS, (2) г dr Rгxл г , где в — коэффициент массоотдачи от жидкости; Кг - газовая постоянная газа; Т -абсолютная температура; АРг- перепад парциальных давлений газа; рг- плотность газа; S - площадь поверхности пузыря.

С учетом выражений для объема газово- го пузыря

V = -uR3

з и площади его поверхности

S = 4uR2

из (2) получим: dR р

^Р гТг = R^ ^P'

Коэффициент массоотдачи к поверхности пузыря определяется уравнением Буссинеска [3]:

Sh = 1,13Re ^1/2 • Sc ^1/2 ,            (6)

гдеSh = ^^ - число Шервуда; Re = -^п— О                            - ж

- число Рейнольдса; Sc = -— - число Шмидта; d_n = 2R - диаметр пузыря; D - коэффициент диффузии биогаза в жидкости; V п – относительная скорость пузыря в жидкости.

С учетом (6) преобразуем уравнение (5)

к виду:

• — = к_ж Й^1/2 ,                (7)

dr      ж^К-¹

где к ж = 1,13( - ) ^1/2 •КТ^ — коэффици— ент пропорциональности, зависящий от режимных параметров.

Проведем моделирование процессов теплообмена в биогазовом реактор е.

Поскольку теплофизические свойства жидкости в слоях 1, 2, 3 существенно отличаются, коэффициенты теплопередачи рассчитываются для каждого слоя отдельно, а затем определяется средний коэффициент теплоотдачи.

Для первого слоя:

Плотность среды:

^Р   Ф^{Р +} (1 -Ф_)Л[ ,   (8)

где Ф – объемная доля твердых взве- шенных частиц; Рт - плотность твердых ча

Ц 1 = !

стиц; р_ж - плотность жидкости.

Динамическая вязкость среды [s]:

рж (1 + 4,5Ф), если Ф < 0,4

Цж            »   „ .(9)

1 _-Ф 1/з ,е^слиФ^ 0,4

Теплоемкость и теплопроводность среды: с1 = хтст + (1 — хт)сж ,(10)

А1 = хтАт + (1 — хт)Аж ,(11)

где ст, сж– теплоемкости твердых частиц и жидкости; λт, λж– теплопроводности твердых частиц и жидкости; хт - - массовая доля твер- дых частиц:

р_тф Хт = ------------ ^т Р_ТФ+Рж (1-Ф)

Число Рейнольдса для мешалки:

Re = п м л м ,             (13)

" 1

гдепм - частота вращения мешалки, 1/с; dM- диаметр мешалки, м; v1 = Ц1р1- кинематический коэффициент вязкости.

Число Нуссельта:

Nu₁ =

0,44Re O^,44 Pr₁ ^0,34 (^) ^0Д4 ( Н ^- ) °,⁴⁷ ( 1-т- ) °,³ , (14) где Nu₁ = ^ l ^- -число Нуссельта.

^A i

Коэффициент теплоотдачи:

Wu. A. а = ---

1 О

Аналогично определяются коэффициенты теплоотдачи для слоев 2, 3. Критериальная формула для числа Нуссельта в этих случаях имеет вид [6]:

Nu = 0,36Re M^/3 Pr ^1/3 ( ^ - ) °,¹⁴ ,   (16)

Рст где Цст - динамическая вязкость жидкости при температуре стенки.

Средний коэффициент теплоотдачи:

а.

ср

_ а1Н1+а2Н2+а3Н3

Н

Определим закон изменения температуры реакционной смеси от времени из уравнения теплового баланса:

C ср m общd| = q_yV + клВН⁽( тн — t)

—

ccGc(t — (сн) + крЯРрН(£тн — (н), (18) где тобщ - - общая масса реакционной смеси; V- общий объем реакционной смеси; k коэффициент теплопередачи от теплоносителя к реакционной смеси; (тн- средняя температу- ра теплоносителя в рубашке; (сн

-

начальная

температура сырья, подаваемого в реактор; (н – темп ература наружного воздуха.

ЛО² Г             ТТ

^ общ = — (Р 1 Н 1 + Р 2 Н 2 + Р 3 Н 3 )

V = — Н к =----1---- к 1 +^-+1

«тн ^с «ср

Разделив (18) на с ср т общ , получим:

dr = ^(( тн — t) + S(t — ( сн ) + Q_B + Q n , (22)

где:

. _ клвн A =        , С ср ^ общ	(23)
s = _^с£_ ,	(24)
С ср ^ общ
Q, = -^^^ ,	(25)
С ср ^ общ
= /С р Л- р Н^ тн -^ н )	(26)
С ср ^ общ
Преобразуем (22) к виду:
dr = (В — A)t + S ,	(27)
где: S = А( тн — В( сн + Q , + Q n	(28)
Интегрируя (27) по времени	т при

начальном условии:

t(0) = t ° ,    (29)

получим:

£(т) = t_m + (t ° — t_m)exp[(P — Л)т (30)

Программа, реализующая режимы работы биогазового реактора составлена в среде Mathcad 15.

Результаты моделирования режимов работы биореактора представлены ниже.

На риунках. 2, 3, 4 представлены результаты моделирования реактора при следующих значениях исходных данных: т сН₄ = 0,7 ; СВ = 10%; t_p = 37T; R_H = 0,02 м; D = 1м; Н = 0,3м; Н₂ = 0,5м; Н₅ = 0,2м; Ф = 0,34; р_т = 1800 кг/м ³; с_т = 840 ^ж-; Л_т = 0,9 -Вт-;

• ¹                                кг*К ¹        м*К

  р₂ = 992 кг/м³; р₃ = 868 кг/м³; с₂ = 4200 -ДЖ ; ^{z                   5                  z}           кг*К

  
  

  с3 = 1780 -ДЖ ;   ^3 = 8,94 * 10“3 Па*с;

• ⁵           кг*К          ⁵

Л2 = 0,635 -^; Л3 = 0,109 -^; пм = 0,2 1/с;

м*К              м*К м

ам = 0,5 м; атн = 1500 Вт/м2*К; Лс = 16 -ВТ-;

м*К

5_с = 0,003 м; с_с = 3700 кДж ; G_c = 10^-3 кг/с;

qv = 5000 Вт/м3; кр = 1Вт/м 2*К;

Dp = 1,06 м; tTH = 40Т; tH = 10Т; tCH = 20Т; t0 = 20 T; f = 1,5.

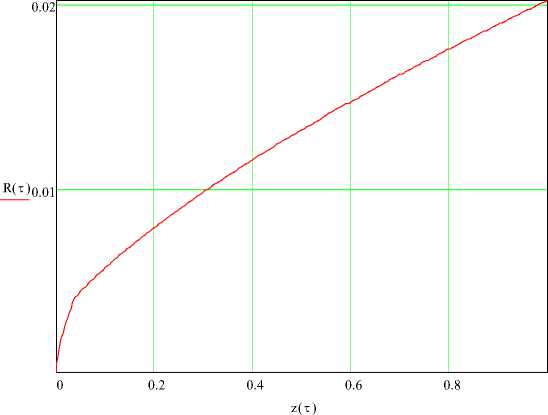
Рисунок 2 - Зависимость радиуса газового пузыря от координаты z

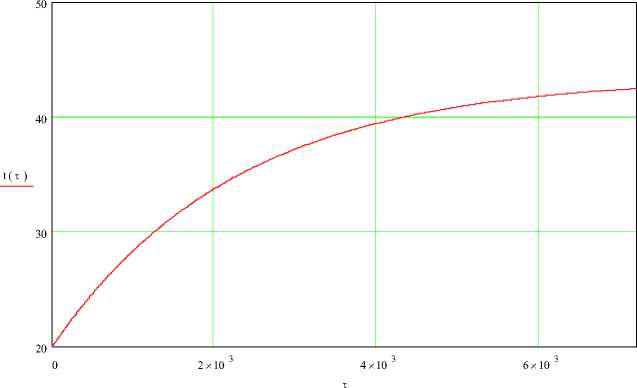
Рисунок 3 - Зависимость температуры реакционной смеси от времени

Газовый пузырь быстро, за время , достигает радиуса            и дальше всплывает с постоянной скоростью (рисунок 1).

Необходимо поддерживать мягкий режим нагревания или охлаждения реакционной смеси, поскольку резкие процессы нагревания-охлаждения неблагоприятно сказываются на жизнеспособности бактерий.

Уменьшение частоты вращения мешалки в 2 раза (до 0,1 1/с) приводит к увеличению времени нагревания реакционной смеси до 40 °С с

4400 до 5100. Увеличение температур теплоносителя с 40 до 60 °С уменьшает необходимое время нагревания реакционной смеси до 1200.

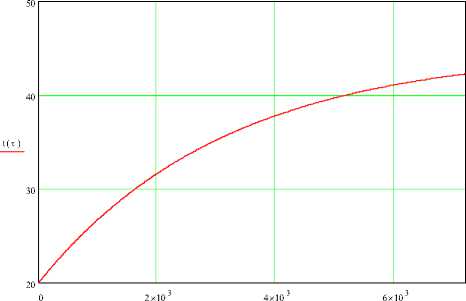
т

Рисунок 4 - Зависимость температуры реакционной смеси от времени при n=1 1/с

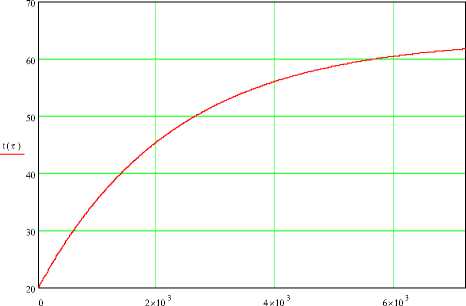
Рисунок 5 - Зависимость температуры реакционной смеси от времени при n м =1 1/с и t тн =60 ⁰С

На рисунке 6 показано влияние средней температуры теплоносителя на необходимое время разогрева реактора.

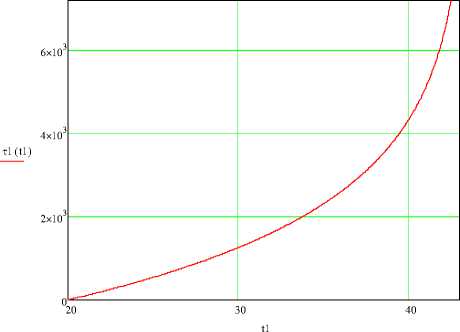
Рисунок 6 - Зависимость времени нагревания реакционной смеси от температуры теплоносителя

Предложенная математическая модель процессов в реакторе анаэробного сбраживания учитывает особенность трехслойной структуры среды в реакторе в зависимости от очевидной разницы и, соответственно, отдельно рассчитываемых значений коэффициентов теплоотдачи и теплопередачи для первого, второго и третьего слоев в реакционном пространстве.

В математической модели учтены различия газовыделений в трех слоях биомассы на основе особенности массотдачи к поверхности образуемого пузырька, генерируемого в процессе биосинтеза газа, при помощи коэффициента массооотдачи в уравнении Буссинеска.

Модель в полной мере построена с учетом зависимости теплофизических и других характеристик слоев и от состава питающей смеси посредством плотности, динамической вязкости, теплоемкости, теплопроводности слоев и частиц, распределенных в биореакторе.

Также в модели учтены гидродинамические характеристики течения реакционной массы в зависимости от интенсивности перемешивания посредством параметров, определяющих значения чисел Нуссельта и Рейнольдса.

При расчете учитывается интенсивность деятельности разновидностей потенциально используемых для анаэробного сбраживания консорциумов микроорганизмов, в свою очередь выбираемых в зависимости от морфологического состава перерабатываемых коммунально-бытовых отходов при помощи введенного коэффициента, учитывающего характер консорциума.

Работа выполнена в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научнотехнологического комплекса России на 20072013 годы» по Государственному контракту от «16» октября 2013 г. № 14.515.11.0089. Статья подготовлена по результатам работ, выполненных на оборудовании ЦКП «КУЭП».