Математическое моделирование трехплоскостной деформации позвоночного столба человека

Одним из тяжелейших заболеваний человека прямоходящего ( Homo erectus ) является трехплоскостная деформация позвоночного столба (сколиоз). В теории и практике есть только два бесспорных факта о данном заболевании – оно проявляется всегда в виде трехплоскостной деформации, возникновение и развитие которой связано с процессом роста [8, 10]. И это при том, что в соответствующей литературе в качестве его причины рассматривается и обсуждается большое количество так называемых «этиологических» факторов [3, 7].

В литературе уже имеется ряд работ [5, 6, 8], в которых на основе различных математических подходов описываются анатомические параметры и характеристики деформированного позвоночного столба с целью решения самой востребованной в клинической практике задачи по объективному прогнозированию развития сколиоза. Однако в указанных работах имеется один существенный недостаток – в их

Балошин Юрий Александрович, д.т.н., профессор кафедры нанофотоники и метаматериалов, Санкт-Петербург

Бобер Степан Васильевич, инструктор-методист лечебно-физической культуры, Санкт-Петербург

Поморцев Иван Юрьевич, сотрудник центра, Санкт-Петербург основе лежит математический анализ базы фактических данных, полученных при клинико-рентгенологической диагностике, но ни в одной из них сколиоз не описывался как процесс.

C точки зрения классической биомеханики нормальный (здоровый, не имеющий деформаций) позвоночный комплекс рассматривается как двухколонное образование [4], состоящее из несущей колонны (24 тела позвонков + 23 межпозвонковых диска) и колонны функциональной (позвонковые дужки, остистые и поперечные отростки, межпозвонковые, или дугоотростчатые, суставы). Первая, несущая (опорная), решает его главную задачу по поддержанию анатомического положения и веса всех органов и систем, входящих в состав туловища, а вторая, функциональная, обеспечивает движения в многозвенном позвоночном комплексе. Последовательно расположенные позвонковые дужки формируют позвоночный канал, в котором располагается спинной мозг. Кроме этого, состояние нормального позвоночного столба определяют граничные условия его существования: 1) вертикальное положение комплекса (колонн); 2) верхние и нижние концы колонн всегда на одном уровне; 3) расстояние между колоннами на любом уровне – величина постоянная.

Однако иерархичность систем органов и тканей, являющаяся фундаментальным условием жизнеспособности организма, заставляет видеть другие «колонны» в позвоночном комплексе. Это спинной мозг как важнейший отдел центральной нервной системы (главной управляющей системы организма) и его костно-связочно-мышечный «футляр». Первый в настоящей работе принимается за дорсальную (заднюю) колонну, а определяющий продольный размер позвоночного столба «футляр» – за колонну вторую, вентральную (переднюю).

Модель 1 и описывающее ее уравнение

С позиций теоретической механики, с учетом вышеизложенных особенностей функционирования позвоночного комплекса, в работе [2] впервые была предложена простейшая математическая модель, которая в первом приближении давала объяснение образованию трехплоскостной деформации в двухколонном позвоночном комплексе.

Ниже (рис. 1) представлена взятая из работы [2] схема образования трехплоскостной деформации в двухколонной модели позвоночного столба. В условия задачи, описывающей сколиоз как процесс деформирования модели, были добавлены определенные требования к отрезкам. Дорсальный прямой ( S , short ) рассматривается как отрезок, не меняющий свой продольный размер O ₁ O ₃, а вентральный ( L , long ) представлен в виде кривой A B A , обладающей свойством менять продольный размер на некоторую величину A L , но при этом любая точка данной кривой равноудалена от отрезка OO на постоянное расстояние r .

Задача была сформулирована следующим образом: имея длину дорсального отдела S , расстояние между отделами r , а также угол поворота φ вентрального отдела L относительно дорсального S , необходимо определить зависимость длины переднего отдела L от трех параметров S , r и φ с учетом вышеописанных ограничений модели.

Для решения задачи рассматривается развертка поверхности цилиндра радиусом r и высотой S , которая содержит кривую L , симметричную относительно оси OB , поэтому достаточно найти длину ее половины и удвоить.

Аппроксимируем кривую L полиномом третьей степени:

y ( x ) = ax ³ + bx ² + cx + d . (1)

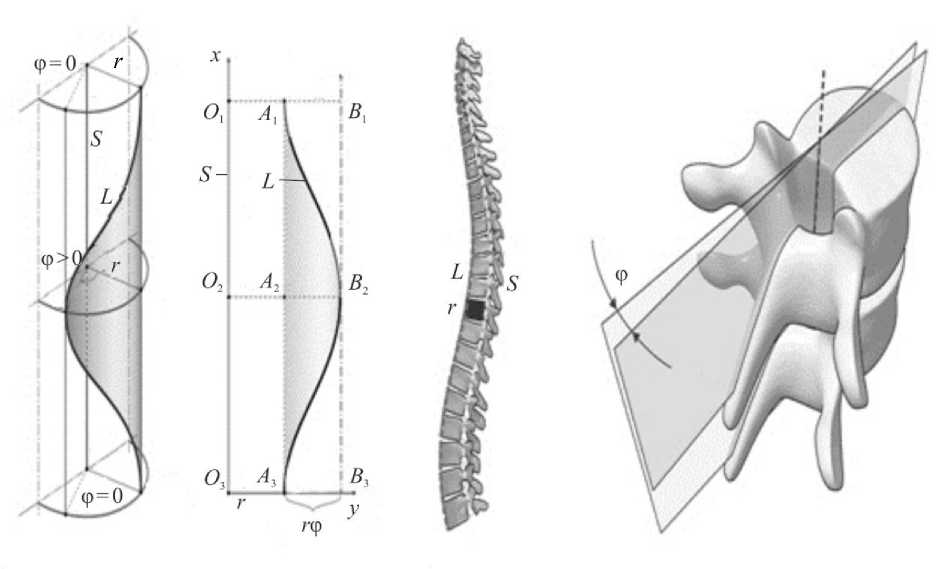
Рис. 1. Схема образования трехплоскостной деформации позвоночника [2]

По формуле нахождения длины кривой, заданной уравнением y ( x )

S

L = 2 J -^1 + y ^adx .

Также, используя ограничения модели, имеем в крайних точках

' У ⁽⁰⁾ = d = r Ф ,

yI 5 1 = y'I 5 1 = 0, 12)    12)

_ y '(0) = c .

Подставив условия (3) в (1) и подсчитав производную, получаем

y ( x ) = ax ³ + bx ² + r ф ; y ' ( x ) = 3 ax ² + 2 bx .                       (4)

Далее, подставив равенства из системы (3) в полином и получив решение системы уравнений, имеем значения коэффициентов полинома

16 r ф a =---;- ;

12 r ф ~1F

Производя несложную замену переменных, получаем производную в следующем виде r- 125      2x

5 = r ф ; kk = —, ^ = — ,                       (6)

У '© = к (f -% ) ; d 6 = 2 dx , x е 0, S

2 x

^^ = — 6

S

Применив данные преобразования к формуле расчета длины кривой (2), получим

L = SJ ^1 + к (^2 -^)2 d^ .

В полученной формуле L – длина колонны, меняющей свой продольный размер, S – длина колонны, не меняющей свой продольный размер; r – радиус вращения, расстояние между L и S (постоянная величина на любом горизонтальном уровне модели); φ – наибольший угол поворота, наблюдаемый при скручивании L вокруг S . Также необходимо обратить внимание на переменную x , по которой производится интегрирование в формуле длины кривой; значения этой переменной являются координатами по оси абсцисс точек кривой L на графике развертки этой кривой

(рис. 1). Для удобства расчетов данная переменная была заменена на £ = ^ x

.

Математическое моделирование, представленное в данной работе, имеет своей целью дальнейшее развитие идей работы [2] для более качественного объяснения закономерностей образования трехплоскостной деформации позвоночного столба.

Прежде всего был произведен численный анализ формулы (8), который дал возможность в прикладных целях получать значение угла φ в зависимости от значений остальных параметров системы (см. рис. 1).

Интеграл в формуле (8), вероятнее всего, невозможно вычислить аналитически. Однако, используя численные методы, можно анализировать этот интеграл как некоторую зависимость

• — = F ( к ) = j J1 + к ^² -^) d ^ .   Если быть точнее,

S 0

анализироваться будет в первую очередь F ² ( k ). При исследовании этой функции в различных диапазонах удалось выявить следующую ее особенность: с относительно небольшой погрешностью она очень неплохо аппроксимируется линейной функцией ак + b.

В частности, при к е [ 0, 40 ] график F ²( к ) имеет вид, представленный на рис. 2. После аппроксимации на данном интервале значения коэффициентов получились такими: a = 0,031092491; b = 1,000022401.

Общий вид графика изменения погрешности A F ²( к ) = | F ²( к ) - ( ак + b )| представлен на рис. 3. Как можно заметить на рис. 3, при k = 16 достигается наибольшее отклонение, составляющее примерно 15 %.

Далее, получив неплохую аппроксимацию для F2 (k), возвращаемся к F(k). Предполагаем, что, если квадрат функции можно неплохо аппроксимировать линейной функцией, вероятно, саму функцию можно неплохо аппроксимировать функцией квадратного корня: F(к) = Vак + b = aa. + + —=ак+в.. Вновь применяя численный a метод на интервале к е [0, 40], получаем такие значения коэффициентов:

а = 0,1763306; р = 32,1628267.

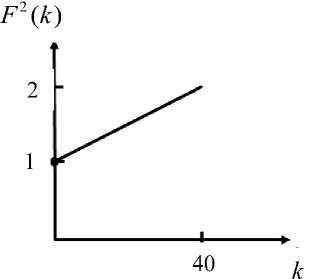
Рис. 2. Функция F ²( к ) в интервале к е [ 0,40 ]

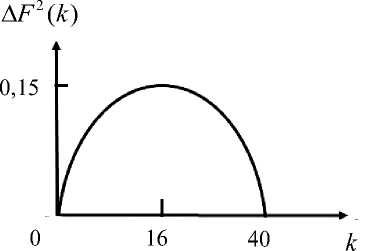
Рис. 3. Изменение погрешности A F ²( к ) в интервале к е [ 0,40 ]

При этом погрешность этой аппроксимации  AF (к) = F (к) - (ak + b )|  не превышает 6,3 %.

Таким образом, мы аппроксимировали с погрешностью, не превышающей

L

[ 0, 40 ] (сами значения

• 6,3 %, функцию F ( к ) = — функцией a^jк + в на интервале к е

функции на этом промежутке были в диапазоне от 1 до 1,5 – примерно этот диапазон соотношения L и S и интересен с точки зрения медицины).

Далее, используя равенство

L = ^а у ^ +р

и замены (6), после несложных

преобразований можно записать значение ф в следующем виде:

„       ¹       I т 2     2 с*2п2

ф =---- LL —a S р

12a-r               ’ при этом a и р являются некоторыми вычисленными константами, которые, в свою очередь, зависят от отношения     и в общем случае находятся в диапазоне a~ 0,175 — 0,185; р* 30 — 32.

Благодаря численному анализу формулы (8) удалось также построить графики зависимости разности A L длины вентрального отдела L и дорсального отдела S от угла поворота φ при условном расстоянии между отделами r в 2,5 см (рис. 4).

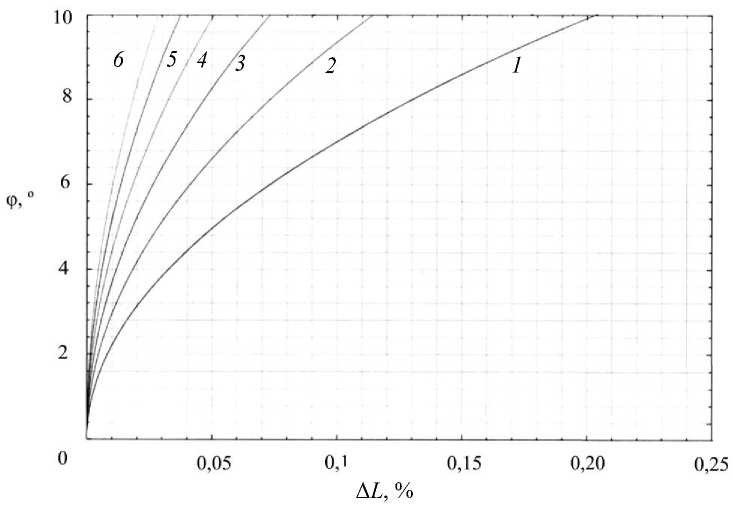
Рис. 4. Зависимость разности длины Δ L вентрального отдела L и дорсального отдела S от угла поворота φ при условном расстоянии между отделами r в 2,5 см

Идентичность картин в математической модели и в реальном позвоночном столбе дает основание предполагать идентичность механизма их инициации [3, 4]. Поэтому появляются основания считать, что, продолжая исследование математической модели, можно будет найти те закономерности в развитии реального сколиоза, которые в экспериментах и опытах на животных не обнаруживались [1].

Уравнение и модель 2

Однако в реальном позвоночном столбе изначально имеются физиологические сагиттальные изгибы – грудной кифоз (средняя величина примерно 165–170°) и поясничный лордоз (примерно 150–170°) [4], на протяжении которых можно видеть изначальное различие ( ± Δ L ) между продольными размерами длин вышеуказанных отрезков (колонн) L и S . В грудном отделе это – Δ L , а в поясничном + Δ L .

На рис. 5 представлена модель реального позвоночного комплекса в сагиттальной плоскости. Она описывается двумя параллельными кривыми S -образной формы с постоянным расстоянием R между ними. Вентральный отрезок L состоит из L киф + L лрд , а дорсальный S из S киф + S лрд . При этом повторим, что L киф – S киф = – Δ L киф , а L лрд – S лрд = + Δ L лрд . Каждая из сагиттальных прямых («кифоз» и «лордоз») имеют радиус R киф и К лрд .

Таким образом, для описания процесса в реальном позвоночном столбе уравнением (1) должно произойти устранение – Δ L киф и + Δ L лрд . Это явление и можно наблюдать у реальных больных. Речь идет о симптомокомплексе так называемой «плоской спины».

Переход модели с заложенными в нее физиологическими сагиттальными изгибами, представленной на рис. 5, в строго прямое состояние (см. модель на рис. 1) математически может быть описан уравнением (9) с учетом уравнения (8) как

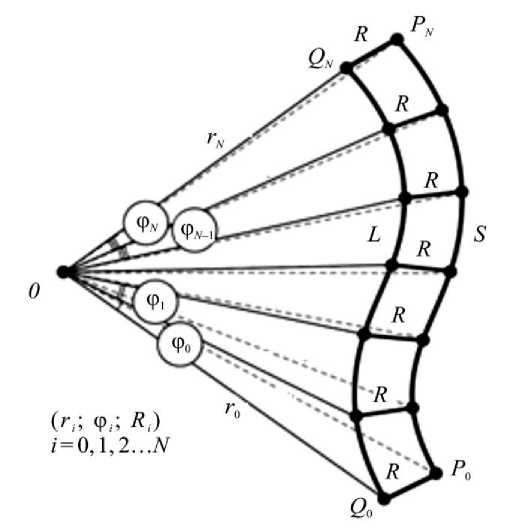
Рис. 5. Модель реального позвоночного комплекса в сагиттальной плоскости

N

^{A L} = s ^

= 0

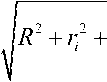
2 R • r² rFF+^^S

—

z

Охарактеризуем кратко математическую модель, в рамках которой получена формула (11). На рис. 5 показаны две кривые L и S в полярных координатах. Рассматривается разбиение этих кривых точками ( Q , P ) . Отрезки, которые образованы каждой из пар ( Q , P ) , имеют длину r , они перпендикулярны касательным к кривым L и S в точках Q и P . Предполагается, что есть возможность интерполировать кривую S функцией r ( ф ) , и разбиение будет производиться по достаточно малым промежуткам. Рассмотрим некоторый сегмент OPQ P Q (рис. 6).

По теореме косинусов

R ² = R ² + r ² - 2 R • r • cos(90 + 0_z) = R ² + r ² + 2 R • r • sin 0_z.              (12)

Используем простые тригонометрические соотношения sin 0z

1 + ctg² 0 _z. ’

r ' ( ф )

^{r (}ф1-_ф = r • ctg ⁰ ^ ⁰ = ^arcctg i , ^{ф ф}

r подставим их в формулу (12) и получим

R =

2 R • r r

' R ^ + r ^ +  ,         i

N

Далее, L = ^ R ф, ^ A L = L - S - получаем формулу (11). i = 0

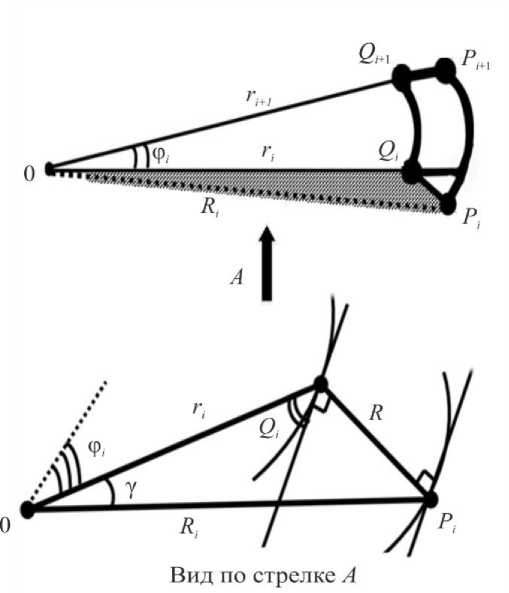
Рис. 6. Пояснение к математической модели (11)

Уравнение (11) помогает решить задачу о том, на какую величину Δ L необходимо удлинить часть вентрального отрезка L киф в грудном кифозе и уменьшить соответствующую часть в поясничном лордозе L лрд , чтобы позвоночный комплекс стал прямым.

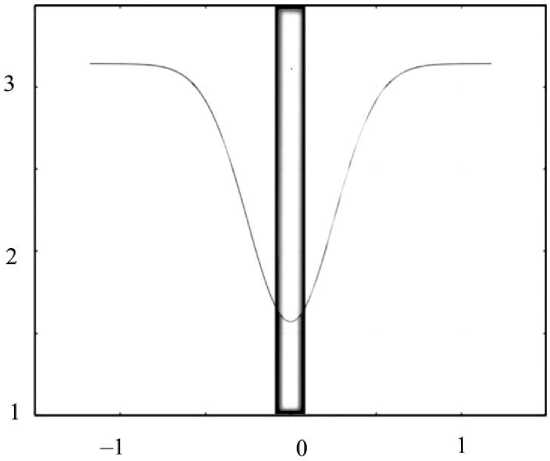
На рис. 7 представлен результат численного решения уравнения (10), устанавливающего взаимозависимость угла наклона модели позвоночного комплекса от изменения соотношения между вентральной и дорсальной колонами. На рис. 7 видно, как при постепенном увеличении продольной длины меньшей колонны модель, представленная на рис. 5, стремится в сагиттальной плоскости к условному выравниванию L = S , приближаясь к вертикальному положению, а далее на небольшом отрезке значений (при достаточно малых величинах Δ L находится в пределах от –0,125 до +0,125 см при угле φ ≈ 1,65 рад) достигает его (пик графика, заключенный в прямоугольник). После этого модель начинает скручиваться в вентрально-дорсальном либо дорсально-вентральном направлении, достигая максимума в крайних значениях графика, представленного на рис. 8.

Заключение

На основе вышеизложенного математического моделирования, можно сделать следующий вывод: трехплоскостная деформация является ничем иным, как ответом на разновеликость двух отрезков (колонн), имеющих строгие граничные условия, которые определяются анатомо-постурологическими условиями функционирования реального позвоночного столба. Главные условия – это вертикальное положение, неизменный уровень верхнего (краниального) и нижнего (каудального) концов колонн и неизменность (постоянство) передне-заднего расстояния между компонентами позвоночного комплекса. При этих условиях излишки длины одного из отрезков

φ, рад

Δ L , cм

Рис. 7. Зависимость угла наклона φ позвоночного комплекса от увеличения продольной длины Δ L короткой дуги

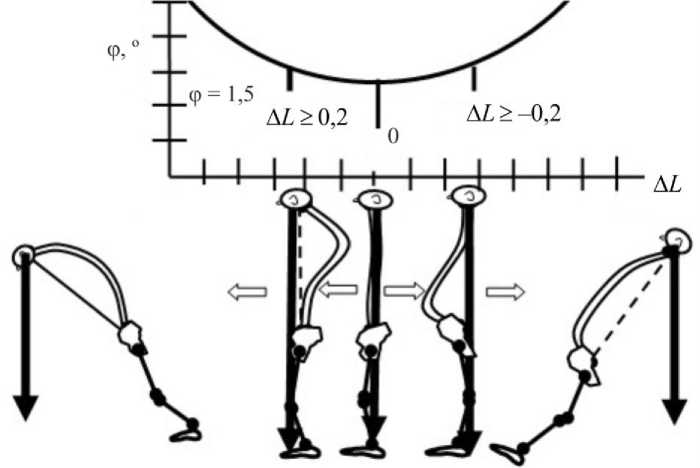
Рис. 8. Динамика изменений конфигурации модели позвоночного комплекса относительно графика на рис. 4

(колонны) компенсируются его скручиванием вокруг короткого (отрезка, колонны). Другой ответ на вопрос о причинах происхождения трехплоскостной деформации теоретическая механика исключает.

Однако в реальном позвоночном столбе имеются анатомо-физиологические особенности, которые противостоят прямому применению такого вывода, поскольку процесс скручивания возникает только при условии прямолинейности отрезков (колонн). Но и здесь рассмотренное математическое моделирование позволяет описать устранение заложенных в модель изгибов, аналогичных физиологическим грудному кифозу и поясничному лордозу.

При таких условиях совокупный процесс образования трехплоскостной деформации в двухколонной модели, приближенной к реальному позвоночному столбу, можно представить как итоговый результат двух самостоятельных процессов. Сначала излишки длины одного из отрезков «поглощаются» введенными в модель изгибами. По исчерпании этого резерва начинается процесс скручивания длинной колонны вокруг короткой, что по внешним характеристикам делает модель совершенно идентичной реальному сколиозу. Другими словами, сначала наблюдается процесс, описываемый уравнением (11), а затем уже процесс, отвечающий уравнению (8).

Предлагаемое математическое описание процесса трехплоскостного деформирования двухколонной модели позвоночного столба открывает новые перспективы не только в понимании патогенеза сколиоза, но и при планировании лечебных подходов, поскольку начинают просматриваться ключевые патогенные звенья и мишени, воздействие на которые может привести к успеху в противостоянии сколиозу.