Математическое моделирование трудовых процессов в производственных системах

Запишем общую математическую форму задачи выбора решений в рассматриваемых условиях. Для выбора предварительного решения необходимо выполнить включение х0 ∈ Х(ω) для всех ω ∈ Ω и обеспечить высокую начальную эффективность системы, поскольку некоторые компоненты решения не подлежат корректировке. Этим требованиям удовлетворяет следующая задача:

КX°) = max f ( X ), где X ° = ^П X (to ); X e X 0             ®e^

f ( x ) = inf f (x , to ). meQ

Задача (1) выбора решений на предвари -тельном этапе может оказаться сложной, а в ряде случаев неприменимой на практике (например, если Х0 – пустое множество). В такой ситуации используются другие постановки задач поиска предварительного решения в сочетании с операцией проектирования предварительного решения на множество Х(го). Кроме того, для точной оценки условий работы исполнителей требуется оценка эффективности предварительного решения, которая может быть получена в конце периода планирования.

Рассмотрим задачу принятия решений на втором этапе. Для любого го е □ введем показатель максимально возможного эффе кт а корректирования предварительного решения ∆ ( х ⁰, ω ): А ( x °, t o ) = max f ( x , о ) - f ( x ⁰, co), A ( x ⁰, о ) > 0. (2) x e X ( o )

Если для некоторых ω ∈ Ω неравенство (2) будет строгим, то исполнитель может повысить результат оптимизации, он будет заинтересован выполнить эту функцию, так как поощрение будет больше трудозатрат на коррекцию предварительного решения. Следует отметить, что максимально возможный эффект корректирования решений соответствует оптимальному решению х^* ∈ Х ( ω ) в рассматриваемой иерархической системе.

Пусть А (х, х0, го) = f(x, го) -f(x0, го), х е Х(го) – величина дохода в системе в единицу времени за счет коррекции предварительного решения. Через показатель а е [0 - 1] обозначим коэффициент разделения дохода от коррекции решения между центром (интересы системы в целом) и исполнителем (интересы нижнего уровня управления, а также частные интересы). Тогда задача второго этапа имеет следующий вид:

• 1.    Задача центра:

• 2.    Задача исполнителя:

M (ст, x ) =стА( x , x ⁰,to)-р (А( x , x ⁰,ю)) — max . (3) x e X (to)

M0(ct ,x)=(1 -ст ) A(x, x°,to)^ max сте [0-1],(4)

где ф (A( x , x 0 , to )) - функция трудозатрат исполнителя в процессах корректирования предварительного решения, которая как предположение зависит только от значения функции ∆( x , x ⁰, ω ).

Таким образом, на рассмотрение принята иерархическая система принятия решений, механизм функционирования которой описан выражениями (1)–(4). По нашей классификации система является одностадийной непосредственно агрегируемой, с агрегатом A = А ( x , x 0 , to ), х е Х ( to ).

При исследовании иерархических систем математическая модель (1)-(4) играет роль элементарной системы, конкретизация которой позволяет получать теоретические и прикладные модели систем с многими центрами принятия решений. Отношения в системе легко восстанавливаются путем анализа выражений (1)-(4). Главные функции центра состоят в выборе предварительного решения и нахождении уровня вознаграждения исполнителя при решении игры (3)–(4).

Функции исполнителя сводятся к выбору уровня корректирования решения в соответствии с назначенным вознаграждением и поиску скорректированного плана (выражение (4)). Реализацию процесса корректирования решений центр и исполнитель осуществляют совместно.

Пусть f ( x , ω ) является непрерывной по x для любого ω ∈ Ω, а множество Х ( ω ) – компактно. Тогда множес тв о значе н ий агрегата ∆ совпадает с отрезком [0 – ∆( x ⁰, ω )], ∆( x ⁰, ω ) ≥ 0. Центр должен выбирать для каждого to е Q стратегию поощрения в классе функций σ : [0 – ∆( x ⁰, ω )] → [0 – 1]. Тогда декомпозиция игры (3)–(4) имеет вид (7).

• 1.    Задача центра:

• 2.    Задача исполнителя:

• 3.    Задача корректирования решений:

M ⁰( ст , А ) = (1 -ст ) А — max            (5)

СТЕ [0 - 1]

M ( ст , А ) =стА-ф ( А ) —       max .          (6)

Ае [0- А (x0, to)]

IA K -A ( x^K , x ⁰, co ) | = min IA K -A ( x , x °, co ) I = 0 , ⁽⁷⁾ x e X ( o )

где AK - оптимальная стратегия исполнителя в игре (5)–(6).

Рассмотрим условия применимости модели корректирующей оптимизации в исследовательских целях, а также в решении прикладных задач. Данная модель является адекватной реальным процессам принятия решений, если вектор параметров ω ∈ Ω, неизвестный центру на первом этапе, является постоянным в период планирования. Для производственных систем это могут быть цены на сырье и готовую продукцию, параметры технологического процесса, уровни реальных затрат труда и материалов при производстве промежуточных и конечных продуктов, возможности инновационного развития, новые организационные формы выполнения работ.

Для промышленных предприятий с использованием модельного описания можно решить следующие задачи:

• 1.    Регламентировать рациональный уровень информированности центрального органа управления, оценить потери оптимальности управления в условиях неполной и асимметричной информированности центров принятия решений.

• 2.    Разработать системы оплаты и стимулирования труда, согласованные с целями системы в целом и рыночными условиями привлечения рабочей силы.

Функциональная структура системы управления персоналом

Структура процесса принятия и реализации решений в рассматриваемой системе приведена на рисунке [1-4]. К традиционной системе управления персоналом (задание целей, планирование действий, информационное обеспечение, реализация решений и др.) добавилась функция управления активностью исполнителя [5; 6]:

• -    контроль результатов деятельности исполнителя;

• -    оценка фактического результата;

• -    целевое информирование исполнителя, предполагающее сообщение исполнителю о целях управления в системе, его роли в данном процессе, программе управления, что необходимо для оценки результатов деятельности, разработки нормативов, процедур контроля, методик вычисления оценок полученных результатов, принципов поощрения и наказания. Информирование должно осуществляться в «человеческих формах» и быть опережающим по времени (на рисунке информационные сообщения данной функции выделены пунктирной стрелкой) [7; 8];

• -    расчет нормативного результата;

• -    формирование фонда оплаты труда и стимулирования исполнителя в зависимости от нормативных и фактических результатов.

  

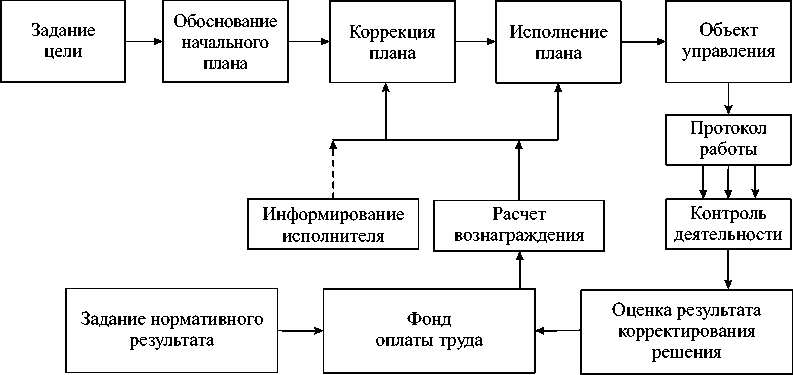
  Структура принятия решений в системе управления персоналом

  
  

В данной структуре исполнитель выполняет следующие функции:

• -    коррекция плана, которая сводится к оценке рационального для него уровня корректирования (рационального уровня активности) в реализованной центром системе вознаграждения и обоснованию корректирующих решений;

• -    исполнение (реализация) скорректированных плановых решений.

В настоящее время научные основы управления в иерархических системах только формируются, поэтому данная структура применима не во всех случаях управления персоналом. Тем не менее рекомендуется использовать данную структуру на практике.

Общие принципы моделирования неосвоенных трудовых процессов

Проблемы синтеза управления персоналом для простых развивающихся иерархических систем ограничены разработкой конкретных вариантов моделей стимулирования. Рассмотрены три типа базовых иерархических систем, в которых развитие осуществляется за счет совершенствования оборудования, изменения технологии работ и квалификации персонала [9; 10]. При этом возможна ситуация общей деградации систем.

В качестве примера приведем модель стимулирования процессов освоения оборудования.

Пусть для N периодов функционирования иерархической систе м ы динамика предельных производительностей ∆ оборудования задана уравнением

∆ = Rj (∆j – 1, τj), j = 1,…, N, где τj – затраты личного времени исполнителя на совершенствование оборудования в период j.

Введем векторы σ = ( σ ₁,…, σ_N ) коэффициентов разделения доходов (стратегия центра) и ∆ = (∆₁,…, ∆ _N ) фактических производителей оборудования.

• 1.    Задача центра:

• 2.    Задача исполнителя:

N

M ₀ (о , А,t ) = X (1 -о j ) Tj A j >   max;    (8)

j =1                  о j e[0,1]

j' = 1, ..., N .

N

M ( a , A , т ) = Z [ a j T j A j -ф, ( A j , A j ) -ат j — max; _(9) j ।                              0 j j

⁰ j < Tj;

j = 1, ..., N .

где T_j – длительность периода j ;

• α – цена личного времени исполнителя;

T ⁰ _j – фонд личного времени исполнителя в период j = ( j = 1,…, N ). Остальные обозначения совпадают с обозначениями в выражениях (5)–(7).

Модели (8), (9) позволяют установить отношения в иерархических системах, при которых освоение оборудования обеспечит повышение эффективности системы. Отметим, что данную модель можно использовать для проверки адекватности моделей стимулирования, поскольку в научной литературе имеются детальные результаты исследования процессов освоения производства. Кроме того, может быть поставлена задача разработки методов идентификации параметров моделей и численных схем поиска оптимальных стратегий центра, которую эффективнее вести в диалоговом режиме.

Прикладные модели трудовых процессов

Основные модели трудовых процессов основываются на модели корректирующей оптимиза- ции. Исследования проводятся с целью обоснования моделей стимулирования и изучения свойств трудовых процессов.

Интерпретировать форму целевой функции исполнителя можно как аналог «прибыли» исполнителя, который получает разность оплаты труда f(и ) и трудозатрат ф ( и ) в зависимости от интенсивности труда и стремится максимизировать этот «доход». Модель принятия решения можно рассмотреть по двум критериям: f ( υ ) и – φ ( υ ) – с простой их сверткой: M ( υ ) = f ( υ ) – φ ( υ ), в которой учитываются критерии с одинаковыми весовыми коэффициентами [11; 12].

Результаты

В наших исследованиях принимаются, во-первых, разные весовые коэффициенты; во-вторых, модель поведения рекомендуется для описания типовых исполнителей, а также в качестве средства для анализа устойчивости механизмов стимулирования в отклонениях; в-третьих, моделирование базируется на принципе «отражающей системы», который формулируется следующим образом: «ценность» оплаты труда и «тягость» труда - субъективные для индивидуума и группы индивидуумов отражения реальности. Персонал стремится максимизировать оцениваемую им оплату и минимизировать ожидаемые трудозатраты. Следуя принципу «отражающей системы», в моделях необходимо использовать не объективную денежную оплату труда и объемы трудозатрат, а воспроизведенные людьми величины, которые могут существенно отличаться от общепринятых. В рамках принципа «отражающей системы» можно объяснить многие парадоксы в экономическом поведении людей.

Рассмотрим один из способов оценки весовых коэффициентов в целевой функции типового исполнителя следующего вида [13]:

M ( υ ) = f ( υ ) – δ ∙ φ ( υ ); υ ∈ [0, υ ].

Пусть для данного трудового процесса найдена методами нормирования труда и . - нормальная интенсивность. Обычно при нормировании труда используется сдельная оплата:

f <°> ^ ’ где P0 - ставка заработной платы, норма выработки υi.

Появляется возможность оценки параметра δ из равенства реального и расчетного поведения. Пусть ~ ( 5 ) = arg max { fи ) - 5ф ( и ) / и е [0, и ]. Тогда искомая величина 5 - корень уравнения ~ ( 5 ) = и .

Если трудозатраты пропорциональны отрицательному логарифму

" ln (1 "Я, то δё = Р0(1 / КН – 1), где КН = υН / υ.

Если функции υ / ( υ – υ) , то δ_ã = Р ₀(1 – К_Н )² / К Н . В этом случае нет необходимости идентифицировать трудозатраты и использовать принцип отражающей системы, поскольку для типового процесса применяются проверенные на практике методы нормирования труда. В дальнейшем в конкретных моделях часто применяются две следующие функции трудозатрат [14; 15]:

Ф _ё (и) = -5 ё I n [ 1 -^ ^и Ф_а ^{( и} ) = ⁵ _а« / ^{( и -} у )•

Для моделей оплаты и стимулирования труда следует предложить показатели, по значениям которых можно оценить работоспособность моделей, их соответствие социально-экономическим рекомендациям. Информативными выступают показатели соответствия оплаты затраченному труду и нормальности трудозатрат в трудовом процессе. На практике необходимо наличие граничных значений показателей, которые могли бы участвовать в оценке работоспособности той или иной системы оплаты труда. Применение на практике результатов исследования теоретических моделей трудовых процессов решает проблемы идентификации параметров, оценки адекватности и работоспособности простых моделей оплаты и стимулирования труда, в которых имеется возможность использования результатов нормирования труда. Все вышеперечисленные аспекты для сложных моделей развивающихся иерархических систем требуют дополнительных исследований [16].

Рассмотрим конкретные модели простых иерархических систем, перечень которых приведен в таблице 1. Результаты и методы исследования представим для конкретных случаев.

Модель исполнения поручений. Пусть персоналу поручается работа объемом Н 0 . Центр стимулирует исполнительность персонала, назначая штраф f(H 0 , и ), зависимый от H 0 и и е V - соотношения порученного и фактического объемов выполненной работы.

Пусть φ ( υ ) – функция трудозатрат. В качестве стратегии центра примем P – частоту контроля исполнителя P ( P е [0, 1]), причем факт контроля считаем для исполнителя случайным образом. Получаем следующую игру, где игроки стремятся минимизировать свои издержки:

Г ≤ [0, 1], V , H ₀ ( P , υ ), V ( P , υ ) = P ∙ f ( H ₀, υ ) + φ ( υ ) >. (10)

Модель контроля сообщений является част-	следующая: φ ( ε ) = b / ε , тогда в (22) V = [0, ε ], где ε
ным случаем модели (10). Пусть исполнитель,	- предельная ошибка сообщения, за которой дей-
которому поручено сообщить S 0 состояние си-	ствуют административные методы управления, а
стемы, искажает информацию до величины S .	B
Введем е = || S 0 - S || - ошибку сообщения - и рас	M ( P , Е ) = P Е Н--,
смотрим функцию M ( P , е ). Пусть центр предъяв-	b где в = — - единственный параметр модели
ляет исполнителю штраф, пропорциональный ве-	d
личине ошибок: ( f ( ε ) = dε ), а функция трудозатрат	исполнителя. Таблица 1

Свод результатов моделирования трудовых процессов

Название моделей	S сЗ н о Рч К Рч О н и К	н о g 5 м о <	Й о К Рч к	Стратегии игроков			S к о Н о О	о Й Рч ^ и -&
				Г 1	Г 2	др.
Исполнение поручений	+	–	–	+	+	+	–	+
Контроль сообщений	+	–	–	+	+	–	+	–
Экономия ресурсов	+	–	+	+	+	+	+	–
Экономия ресурсов для коллективной формы организации труда	+	—	—	+	—	—	+	+
Оптимизация размера коллектива	+	+	+	–	–	+	–	+
Норма (базовый вариант)	+	+	+	–	–	+	–	–
Псевдонорма	+	–	+	+	–	+	–	–
Освоение оборудования	+	+	+	+	–	–	+	+
Пересмотр псевдонорм по инициативе центра	+	—	+	+	—	—	—	—
Пересмотр псевдонорм по инициативе исполнителя	+	+	+	–	+	–	–	–
Пересмотр норм от фактических выработок	+	–	+	+	+	–	–	–
Управление квалификацией	+	–	–	–	–	–	–	–

Рассмотрим оптимальные стратегии игроков и продолжим интерпретацию модели. Ее анализ показывает, что игра Г ₁, распространенная в теории иерархических игр, в данном случае дает систему отношений между игроками, не реализуемую на практике, в силу того что ошибка ε центром не оценивается.

Обсуждение . Рассмотрим стратегии игроков в игре (10), получаемые при механизме Г ₂.

Утверждение 1. Пусть в модели контроля сообщений M0 (P, ε) монотонно возрастает по P и ε, а исполнитель доброжелателен к целям центра; ε > 0, B > 0. Стратегия центра P(ε) устанавливает зависимость частоты контроля P от погрешности сообщения, которая возникает в системе в связи с тем, что цели центра и исполнителя не совпадают. Здесь также видна нереализуемость стратегии, поскольку в любой реальной ситуации невозможно точно проверить равенство ε = ε0. Однако в большинстве реальных систем можно заменить это равенство на строгое неравенство е < е0, при чем эта замена показывает, что функцию наказания исполнителя за излишнюю исполнительность организационная структура не выполняет. Это замечание может не относиться к тренажерам операционных возможностей персонала.

В работе [17] рассмотрены особенности функционирования организационного механизма и показано, что центру необходимы две системы контроля сообщений, сформулированы требования точности этих систем. Полученные выводы справедливы для всех моделей контроля сообщений, в которых функция f ( ε ) монотонно возрастает по ε , а φ ( ε ) удовлетворяет условиям: φ' ( ε ) < 0; φ'' ( ε ) < 0;

lim р ( s ) = оо .

s >0

Для моделей исполнения поручений найдены в частных случаях выражения оптимальных Г1 и Г2 стратегий центра. Показано, что ситуация (P* = 0, υ* = 0) является минимаксным решением и ситуацией равновесия для игры (17), а также поведение игроков согласно этим стратегиям не соответствует реальным системам.

Модели экономии ресурсов являются частным случаем моделей стимулирования при корректирующей оптимизации. Суть моделей состоит в том, что из стоимости сэкономленного ресурса ( Ö ( υ ₀ – υ ), где Ц – цена ресурса; υ ₀ – расход ресурса в базовый период времени; υ – расход ресурса в режиме экономии) выделяется часть, равная λ ( υ ₀ – υ ), для премирования исполнителей. Приведем пример модели при коллективной форме распределения премии, когда центр контролирует суммарный расход ресурса: υ = υ ₁ + υ ₂ + … + υ_n , где υ_i – расходы ресурсов исполнителя i . Возникает простейшая иерархическая система отношений, анализ которой позволяет выявить закономерность коллективных форм оплаты и стимулирования труда.

• 1.    Задача центра:

M, ( X , и ) = ( О -X )( u_n-v ) — max .    (11)

• ⁰                        0 О

• 2.    Задача всех исполнителей: n

M (Xm,..., v n ) = I [ X ( V q -v ) -ф i ( v i X H max;

i = 1 V i >v q i (12) i =1, ..., n .

Исследования показывают, что для квадратичной, логарифмической функций трудозатрат легко вводится агрегативная форма игры (11)–(12), где центр рассматривает коллектив исполнителей как одного игрока. Агрегирование возможно при выполнении условия целостности коллектива, при котором каждый индивид максимизирует коллективный критерий. Заметим, что постулируемый в теории игр коалиционный критерий требует в реальности механизмов поддержки.

Легко показать, что в игре (11)–(12) одному из игроков выгодно не принимать участия в режиме экономии, получая при этом часть коллективной премии. В работе сформулированы условия целостности коллектива при самоорганизации его членов. Условия состоят в том, что с точностью до субъективных оценок все исполнители, во-первых, признают способ распределения премий справедливым, во-вторых, знают, что каждый исполнитель действительно максимизирует свою целевую функцию в игре (11)–(12).

Пусть Р = λ ( υ ₀ – υ ) – суммарная премия коллектива, а P_i , i = 1, …, n – ее распределение ( P = P ₁ + … + P_n ). Любой исполнитель субъективно оценивает с точностью до множества [ p , pj j размер требуемой премии исполнителя j . Тогда первое условие выполнено, если P_–i^j ≤ P_i ≤ P_i^j , i , j = 1, …, n .

При этом необходима непротиворечивость мнений членов коллектива, т.е. справедливость условий:

P. = max P^J <  P = min p V , i = 1,..., n .

1< J' <  n"^{1      1} 1< J' <  n ¹ ,      ,,

Анализ этих условий следует проводить в рамках предположения о целостности коллектива.

Рассмотрим второе условие. Пусть РФi – фактический вклад исполнителя i в общую сумму премии, а P. (, Pj

– его оценка исполнителем j .

Коллектив будет целостным, если для любых пар ( i , j ) выполнены неравенства: P,. ^ P ® . ^ P . Сформулированные критерии целостности и полученные результаты анализа позволяют объяснить некоторые парадоксы функционирования коллективов и могут оказаться полезными на практике.

В предлагаемых условиях целостности и при данных механизмах их проверки число пар контроля в коллективе равно квадрату числа исполнителей, соответственно, растут затраты на самоконтроль. Возникает проблема оптимизации размеров коллектива с учетом условий минимума затрат на контроль. Задача в простейшем случае ставится следующим образом.

Рассмотрим группу ситуаций в иерархической системе, в которой механизмы управления используют нормы и нормативы. Простейшей является модель сдельной оплаты труда, которая имеет следующий вид (модель псевдонорм):

• 1.    Задача центра:

• 2.    Задача типового исполнителя:

M, ( H , A ) =. 1 - P, . A -> max .

V H )     H >  P o

M H ( H , A) = — A-

max _ .

^H        0

В данной модели Н – псевдонорма (стратегия ц е нтра);

• ∆    – потенциально возможная выработка;

• P ₀    – ставка заработной платы.

В работе [18] получаемый из (13)–(14) способ управления персоналом назван механизмом «мягких» и «жестких» норм. Анализ модели и систем оплаты труда показывает, что в данном случае замена псевдонормы Н на ∆ _H – норму выработки, рассчитанную согласно методам нормирования труда, – является неплохим приближением оптимальной стратегии центра в игре (13)–(14), что иллюстрируется следующим утверждением.

Утверждение 2. Пусть в (13)–(14) функция φ (∆) является логарифмической, P ₀ K_Н < ∆ и b = = P ₀ (1 / К_Н –1), где К_Н = ∆ _Н / ∆. Тогда

M 0( H *, A*) - M 0(A H , A (A H )) =/ – оценка потерь оптимальност мы по отношению к механизм Относите нормы выр			у        ____\2 оптимальные псевдонормы в стратегиях Г 1 . За- ,у 1- k h - PP 0       висимость потерь оптимальности представлена v         у A K H J     в таблице 2. Данный результат показывает хоро- и механизма нор-    шую отработанность на практике сдельной сиу, реализующему    стемы оплаты труда. Таблица 2 льные потери оптимальности от использования аботки в качестве стратегии центра (модель норм)
К Н	Р 0 /∆ Н
	0,100	0,200	0,300	0,400	0,500	0,600	0,700	0,800	0,900
0,1	0,400	0,251	0,161	0,100	0,058	0,030	0,013	0,003	0,000
0,2	0,334	0,200	0,120	0,069	0,035	0,014	0,003	0,000	0,003
0,3	0,271	0,152	0,083	0,042	0,017	0,004	0,000	0,003	0,013
0,4	0,210	0,107	0,051	0,020	0,005	0,000	0,004	0,014	0,030
0,5	0,153	0,068	0,025	0,006	0,000	0,005	0,017	0,035	0,058
0,6	0,100	0,034	0,007	0,000	0,006	0,020	0,042	0,069	0,100
0,7	0,054	0,010	0,000	0,007	0,025	0,051	0,083	0,120	0,161
0,8	0,017	0,000	0,010	0,034	0,068	0,107	0,152	0,200	0,251
0,9	0,000	0,017	0,054	0,100	0,153	0,210	0,271	0,334	0,400
Таблица 3 Коэффициенты d коррекции норм выработки при вычислениях оптимальной псевдонормы

К Н	Р 0 /∆ Н
	0,100	0,200	0,300	0,400	0,500	0,600	0,700	0,800	0,900
0,1	0,333	0,471	0,577	0,667	0,745	0,816	0,832	0,943	1,000
0,2	0,354	0,500	0,612	0,707	0,791	0,866	0,935	1,0000	1,061
0,3	0,378	0,35	0,655	0,756	0,845	0,926	1,000	1,069	1,134
0,4	0,408	0,577	0,707	0,816	0,913	1,000	1,080	1,155	1,225
0,5	0,447	0,632	0,775	0,894	1,000	1,095	1,183	1,265	1,342
0,6	0,500	0,707	0,866	1,000	1,118	1,225	1,323	1,414	1,500
0,7	0,577	0,816	1,000	1,555	1,291	1,414	1,528	1,633	1,732
0,8	0,707	1,000	1,225	1,414	1,581	1,732	1,671	2,000	2,121
0,9	1,000	1,414	1,732	2,000	2,236	2,449	2,646	2,828	3,000

В таблице 3 приведены поправки для случая, если при сдельной системе оплаты труда администрация решает использовать оптимальные псевдонормы. Этот результат считается важным с точки зрения оценки адекватности модели стимулирования (5), (6). Заметим, что модели (13)–(14) P с ней совпадают, если принять □ = -0.

H

Модель освоения оборудования (8), (9) может быть исследована численными методами в стратегиях Г ₁ в варианте механизма псевдонорм. Задача исполнителя при фиксированных псевдонормах освоения решается динамическим программированием.

Рассмотрим частные модели освоения оборудования (см. табл. 1). Модель пересмотра псевдонорм по инициативе центра имеет вид:

IP PI

M _n ( H, А, т ) - I -°---⁰ I A T — max ; ⁽¹⁵⁾

V ^H о ^H )      h >  h ,

M ( H, Д , т ) = ’’'’’ + 5 T ln |1—^— | - ат —    max   ; (16)

H      V Ш     — 0 <д<п

0 <т< T o

П = П 0 + bT ; PTL _ P ₀ T >_m,     (17)

H где Н0 = ∆0 = П0КН – псевдонорма и фактический эффект коррекции решений в базовый период времени;

• П ₀ , П – потенциально достижимые результаты коррекции решений;

bT

• у    =— - параметр модели.

T 0

Остальные величины описаны в выражениях (13), (14) (считаем, что N = 1, индекс j опущен). В модели использована линейная функция развития системы и приняты условия полного возмещения затрат исполнителя на развитие системы (17). Заметим, что (15)–(17) – игра с запрещенными ситуациями. Проведем ее решение.

Утверждение 3. Пусть исполнитель доброжелателен к целям центра, и в описании игровой обстановки (15)–(17) параметры при строго положительных α , P ₀, δ , T ₀ удовлетворяют условию: P ₀ γ ≥ α . Тогда множество стратегий центра не пусто, а оптимальная стратегия имеет выражение:

H * = min

PbT __________Y0__0________ T ( T a -° +5 In I 1 -у ^T ( T ( T

)

П о 1 1 ⁺У - I P 0

P_n +5+a 0 T

Анализ модели и решения показывает, что если P0γ ≥ α, то стимулировать освоение оборудования нецелесообразно. Анализ и интерпретация оптимальной псевдонормы показывают, что она стимулирует перенапряженный труд, что соответствует опыту.

По аналогичным схемам приведем некоторые механизмы пересмотра псевдонорм в зависимости от достигнутого эффекта коррекции по инициативе исполнителя.

Псевдонорма изменяется по формуле:

Н = (1 – β ) Н ₀ + β ∆, β ∈ [0, 1].

В статье исследовались проблемы математического моделирования трудовых процессов и отношений в системе «работник – работодатель». В рассматриваемом подходе работодатель характеризуется признаками, которые не учитываются в других подходах. Во-первых, он не может (или не хочет) описывать производственные и управленческие процессы нижних уровней; во-вторых, обязан обеспечить управляемость системы (оптимальность функционирования производственной системы в целом).