Математическое моделирование устройства для глубокого уплотнения грунтов

Современные дорожно-строительные машины: катки, трамбовки, виброплиты и т. п. – при возведении насыпи из различных грунтов осуществляют послойное уплотнение насыпных материалов толщиной 0,3…0,8 м [1–11].

Для уплотнения грунтов на большую глубину, достигающую нескольких метров: земляное полотно автомобильных дорог, гидротехнических сооружений (дамб, плотин) и другие насыпи высотой до 4–6 м – целесообразно изучить опыт применения оборудования для уплотнения грунтов при строительстве зданий и сооружений [12].

Известны способы уплотнения грунтов с помощью конусных оболочек, внедряемых в грунт с помощью ударных импульсов [12] и методом раскатки [13]. Как показывают исследования учёных из г. Омска и Новосибирска, плотность грунта в результате глубинного уплотнения может быть повышена на 20–25 %, а несущая способность в 1,5–2 раза.

Относительными недостатками применяемых известных конструкций являются большая площадь контактной поверхности рабочего органа с грунтом, достигающая 6 м2, что требует установки гидромолотов большой мощности, и динамическая неуравновешенность механической системы устройства для раскатки котлованов [14, 15] с коленчатым валом и одним конусным роликом (рис. 1).

Кафедра «Колесные и гусеничные машины» ЮУрГУ (г. Челябинск) модернизировала устройство для раскатки котлованов, применив динамически-уравновешенную систему за счет усовершенствования конструкции устройства для глубокого уплотнения грунтов [16] с помощью математического моделирования.

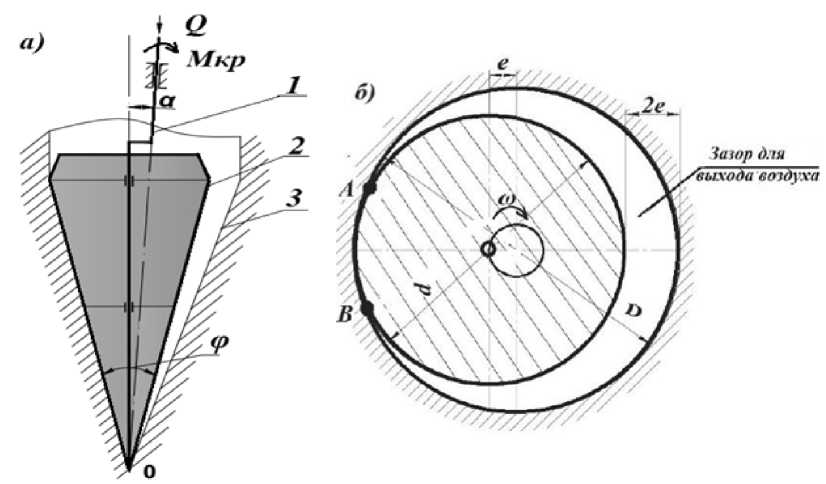
Рис. 1. Схема устройства для раскатки котлованов: а – вид сбоку, б – вид сверху; 1 – коленчатый вал, 2 – рабочий орган, 3 – котлован

Для начала математического моделирования [17, 18] составим принципиальную схему устройства (рис. 2) с изображением сил, действующих на него.

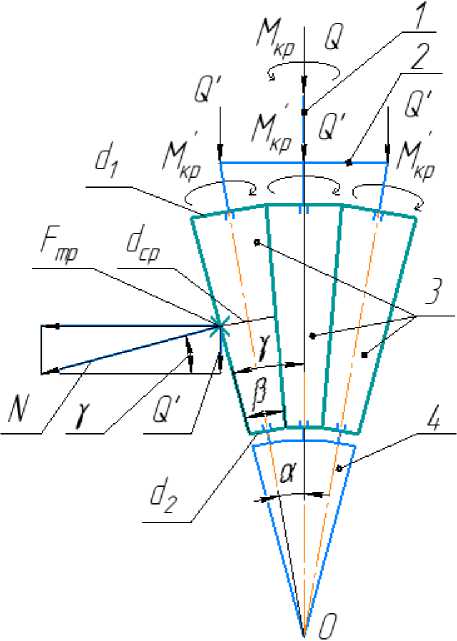
Рис. 2. Принципиальная схема устройства для глубокого уплотнения грунтов

Устройство содержит вал приводной 1, водило 2, конусные ролики 3, расположенные между водилом и забурником 4 под равными углами.

Численные методы моделирования

Из рис. 2 определим половину угла устройства по формуле (1):

У = а + 2 ,                                                                          (1)

где a - угол между центром устройства и осью конусных роликов, град.; ^ - угол наклона образующих конусных роликов, град.

Представим конусный ролик в виде схемы, отображенной на рис. 3.

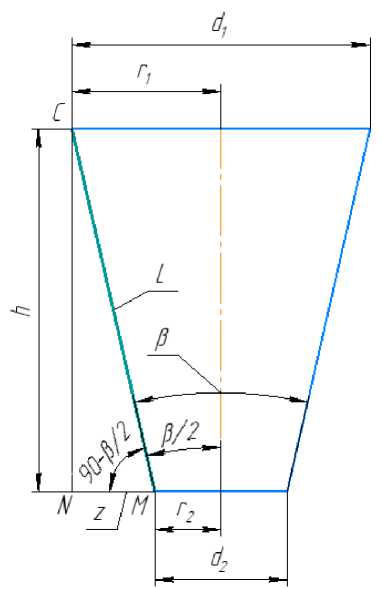
Рис. 3. Принципиальная схема конусного ролика

Согласно рис. 3, определим меньший диаметр d₂. Для начала выразим формулу (2) для определения меньшего радиуса г₂ :

Г2 = Г! — Z,

где г - больший радиус конусного ролика, м; г₂ - меньший радиус конусного ролика, м; z - величина катета NM, м.

Из прямоугольного треугольника CNM (см. рис. 3) определим катет NM через тригонометрическое соотношение углов по формуле:

NM = z = h • ctg (90 — 2 ), где h - величина катета CN, высота конусного ролика, м.

Подставим выражение (3) в (2) и получим формулу:

Г = Г

— h • ctg (90 — 2^

Запишем радиусы г₂ и г через диаметры d₂ и d_! соответственно и получим выражение:

Т = ^-h • ctg (90 - 2у                                                      (5)

После проведения алгебраических преобразований получаем окончательное выражение для нахождения меньшего диаметра d₂ в зависимости от геометрических размеров большего диаметра d_! :

d2 = d! — 2 • h • ctg (90-2), где d! - больший диаметр конусного ролика, м; d2 - меньший диаметр конусного ролика, м.

Согласно рис. 2, определим средний радиус конусного ролика по формуле:

d cp _ d _t+d₂

ГсР = 2 =   4 , где гср - средний радиус конусного ролика, м; dcp - средний диаметр конусного ролика, м.

Согласно рис. 2 определим зависимость между осевой силой внедрения и нормальной силой по формуле:

stay = —, N ’ где Q - осевая сила внедрения, действующая на один конусный ролик, Н; N - реакция опорной поверхности (нормальная сила) конусного ролика на грунт, Н.

Из рис. 3 найдем зависимость между длиной образующей конусного ролика и его высотой по формуле:

cos(f)=7,

где L - длина образующей конусного ролика, м; h - высота конусного ролика, м. Определим длину образующей конусного ролика по формуле:

L = —-

L ™®

Для определения площади контакта конусного ролика с грунтом в котловане воспользуемся схемой, представленной на рис. 4.

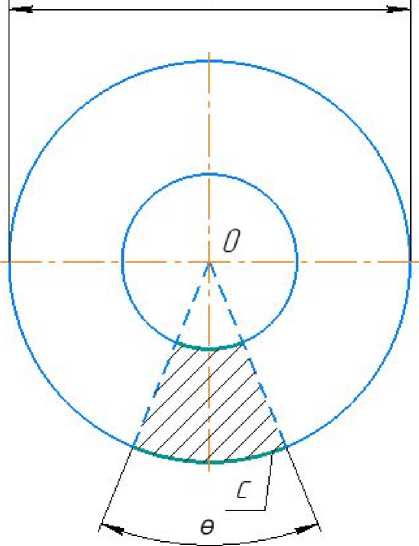
Рис. 4. Принципиальная схема определения площади контакта конусного ролика с грунтом

Составим пропорциональную зависимость к рис. 4:

(360° ^ Я • ^! I в ^ х,

где d^ - больший диаметр конусного ролика, м; в - угол, учитывающий соприкосновение дуги конусного ролика с грунтом, определяется экспериментальным путём, град.; х - длина дуги пло- щади контакта конусного ролика с грунтом, м.

Выразим х из зависимости (11) и представим в виде выражения:

л-d -S X = ---

.

Учитывая формулы (10) и (12), определим площадь контакта образующей конусного ролика

с поверхностью грунта по формуле:

K-dv6-h

S = х • L =------у^.

360°-cos( | )

Численные методы моделирования

Используя формулу (13) и рис. 2, определим реакцию опорной поверхности (нормальную силу) конусного ролика на грунт по формуле:

ff-n-di-0-h.

N = a^S = _o¹ ,_p , 360°-cos( | j где a - напряжение на контактной поверхности конусного ролика, Па.

Найдем напряжение на контактной поверхности конусного ролика по формуле: a = С • у " ,

где С - коэффициент общей деформации грунта, м^ [19]; ц - показатель степени, характеризующий процесс деформации; у - деформация радиуса скважины, м.

Определим силу трения по формуле:

г — f м — f-"-°-^d1-⁰-h

^тр    J • N              /Ох , р            360°-cos(U

где / - коэффициент трения различных грунтов [20].

Согласно формулам (16) и (7), определим необходимый крутящий момент для начала вращения одного конусного ролика по формуле:

М — F

1 1кр    1 тр

f-a-n-d1-0-h-(d1+d2)

• ^ ср =-------------------

1440°-cos( ^ )

,

где М_кр - крутящий момент, необходимый для вращения одного конусного ролика, Нм.

Составим выражение для определения крутящего момента планетарного механизма устройства:

M =

^{М кр}     t kp ,

где i_K p - передаточное отношение планетарного механизма устройства; n - количество конусных роликов.

Выразим крутящий момент, необходимый для вращения устройства, из формулы (18) и запишем выражение:

М кр =

n-f-CT-o-d₁-0-h-⁽d₁+d 2 ⁾-(ty(a+ 2 )-ty( | ))

1440°.C^os( S ). _t5 ( S )

.

Из выражений (8) и (14), заменив угол у значением из (1), определим осевую силу внедрения, действующую на один конусный ролик, по формуле:

Q = N • sin у =

a-n-d1-0-h-stn(a+^

360°-cos^ l ^

.

Составим формулу для определения осевой силы внедрения, действующей на приводной вал устройства:

Q ' = ; .

где Q - осевая сила внедрения, действующая на один конусный ролик, Н; Q - осевая сила внедрения, действующая на приводной вал устройства, Н.

Q = n^Q =

n-o'-o-d₁-0-h-stn(a+ ^ )

360°-cos( l ^

.

Выводы