Математическое моделирование в системах проектирования лекал

Активное развитие отечественных САПР связано с мировой тенденцией и поддержано государственными программами по импорто-замещению и созданию отечественной программной платформы [1] .

Y-4.0

Фактически оно ограничено приоритетными областями (машинострое нием, приборостроением и строительством )1 и не распространяется на лёгкую промышленность [2] .

Современное направление развития САПР для лёгкой промышленности связано с технологиями 3D-моделирования и автоматизированного снятия мерок (параметров манекена) [3 –5] . Передовые исследования в этой области связаны с функциональным моделированием человеческого тела, 3D-дизайном одежды, 3D-драпировкой одежды и анимацией, генерацией из 3D модели 2D шаблона [6 , 7] . Но даже разработчики 3D-систем CAD признают, что швейная промышленность, в конечном итоге, нуждается в 2D-моделях для производства одежды [7 –9] . Поэтому и 3D-системы CAD для одежды желательно снабдить функциями API, обеспечивающими использование традиционных конструкций 2D-моделей [7] . Более того, даже при наличии модуля автоматической генерации из 2D- в 3D-модель, каждый раз, когда изменяются параметры тела (одежды), для генерации 2D-модели необходимо выполнить полный процесс выравнивания. Это делает процесс интерактивного 3D-дизайна ненужным, долгим и утомительным [7] , особенно для индивидуального пошива.

Из вышесказанного видно, что модуль 2D-моделирования по прежнему востребован в САПР для производства одежды. На рынке САПР нет качественных и доступных решений для 2D-моделирования Для индивидуального предпринимателя и для предприятий малого бизнеса 2D-моделирование часто оказывается единственным этапом в производственной цепочке, который подлежит частичной автоматизации. Очевидно, что для предприятий такого малого масштаба промышленная САПР недоступна, да и не нужна. С другой стороны, доступные системы (подсистемы), такие как «ЛЕКО» 2 или «Грация» 3 не удовлетворяют потребностям пользователей, поскольку, хоть и используют алгоритмический принцип конструирования, но не позволяют проводить дальнейшее визуальное компьютерное моделирование с построенным чертежом.

Для индивидуального пошива сейчас доступны либо бесплатные сервисы, как например, «Портной блог» 4 , позволяющие по введённым пользователем размерным признакам строить лекала для уже созданных моделей, либо платные услуги по изготовлению лекал в промышленных САПР, как «Лекало.Про» 5, либо демо-версии САПР с некоторым набором лекал и ограничениями использования ПО («ЛЕКО», «Грация»).

К недостаткам таких САПР следует отнести необходимость изучения специфичного языка программирования (а не только интерфейса и функций для построения лекал) и непереносимость выкроек в другую САПР или векторный графический редактор. Часто разработчики таких систем предусматривают для дальнейшей работы с полученными лекалами использовать другие САПР (например, AutoCAD), стоимость которых намного превышает стоимость специализированных САПР. Кроме того, все имеющиеся на рынке САПР привязаны к конкретному типу производства и методике проектирования одежды [10] . Интерфейс таких САПР и принцип работы с ними свидетельствуют о заложенных в их основу архитектурных стилях, господствовавших в программировании 20–25 лет назад. Не произошло прорыва в этой области и на последней выставке Texprocess 2019 [11] .

Таким образом, есть проблема с насыщением рынка ПО для предприятий малого бизнеса лёгкой промышленности. Все эти факты должны привести к появлению САПР или модулей 2D-моделирования лекал нового поколения.

Однако, самостоятельное решение задачи автоматизации процесса интерактивного параметрического конструирования (с записью алгоритма) для пользователя и для разработчика САПР требует решения нетривиальных задач планиметрии (см., например, [12 , 13] ) и является в общем случае проблематичным.

Анализ типовых процессов

Для определения требований потенциальных пользователей к программной системе рассмотрим типовой бизнес-процесс создания лекал для индивидуального пошива на основе мерок, снятых с конкретной фигуры. Как видно из рисунка 1, первая и последняя задачи не автоматизируются (при индивидуальном пошиве), а расчёт параметров формализован и легко автоматизируется. Параметры рассчитываются на основе полученных мерок и используются в дальнейшем для параметрического моделирования в последующих задачах.

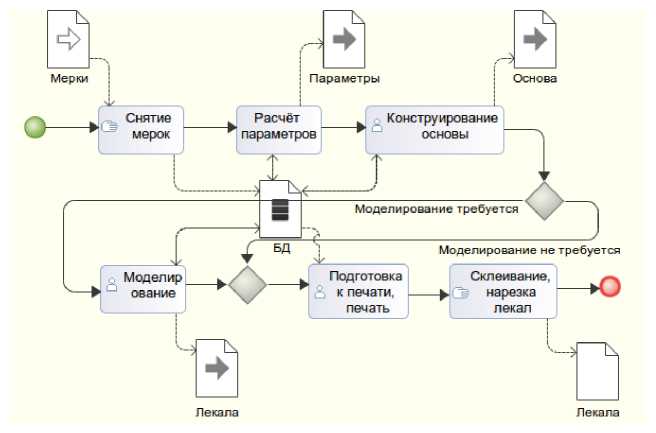
Рисунок 1. Бизнес-процесс построения лекал при индивидуальном пошиве

Подготовка к печати заключается в выборе объектов (части лекал) для печати и иногда — в раскладке (автоматической, ручной, полуавтоматической) на печатном листе. В промышленных САПР эта задача, как правило, хорошо автоматизирована, а для индивидуального пошива можно использовать редактор векторной графики и редактор электронных таблиц. Здесь можно порекомендовать, как один из вариантов, свободное ПО: редакторы Inkscape и LibreOffice Calc. Для наилучшей совместимости рекомендуется хранить результаты моделирования в графических файлах открытого формата SVG. Кроме того, использование открытых стандартов будет способствовать появлению большого количества приложений (программных интерфейсов) для моделирования лекал так же, как и использование API OpenGL для 3D моделирования [7].

Наиболее трудоёмкие задачи в рассматриваемом бизнес-процессе — конструирование основы и моделирование. Конструирование основы заключается в построении базового чертежа по размерным признакам. Моделирование заключается в нанесении дополнительных (т. н. модельных) линий на основу чертежа. На этом этапе на одной основе с помощью моделирования можно создать множество вариаций изделий. Автоматизация этих задач (разработка соответствующих программных модулей) также представляет собой наиболее сложную задачу. Прежде чем приступить к проектированию соответствующих модулей САПР необходимо описать набор графических примитивов и набор графических преобразований (трансформации этих примитивов в результате воздействия преобразований).

Набор графических примитивов должен соответствовать необходимому набору, используемому в расчётно-графических методиках конструирования основы. Эти примитивы сильно отличаются от стан дарта SVG прежде всего сигнатурой (способом задания). Результаты моделирования должны быть преобразованы в стандартный формат SVG. Это позволит открывать, редактировать (вносить мелкие правки), распечатывать в доступных редакторах векторной графики.

Математическое обеспечение таких подсистем (конструирование основы и моделирование) включает в себя аппарат планиметрии для построения и параметрического моделирования геометрических объектов.

Моделирование на этапе конструирования основы

Типовой процесс конструирования заключается в создании основы — базовой конструкции на основе ранее снятых индивидуальных измерений (мерок). Полученная в результате этого процесса основа представляет собой чертёж, который максимально точно описывает форму и силуэт будущего изделия. Качество готового изделия зависит от точности снятых измерений фигуры, от выбранной методики конструирования и правильности расчётов.

Для реализации этой задачи на компьютере могут использоваться различные подходы: визуально-графические, программно-алгоритмические методы и др., которые отличаются интерфейсом пользователя.

Однако, независимо от способа реализации, должен использоваться базовый набор графических примитивов:

• •    точка: p = p(x, y), где x, y — декартовы координаты на плоскости;

• •    отрезок: l = l(p 1 ,p ₂ ), где p 1 , p ₂ — начальная и конечная точки отрезка, соответственно;

• •    дуга: a = a(p 1 ,p ₂ , r), где p 1 и p ₂ — начальная и конечная точки дуги, соответственно, а r — радиус окружности;

• ^•    сплайн (один из вариантов — кубическая кривая Безье):

b = Ь(Р1,Р2 ,Ф1,ф2,к1,к2), где p1 и p2 — начальная и конечная точки сплайна, φ1 и φ2 — углы сопряжения (углы наклона касательных на концах сплайна), k1 и k2 — коэффициенты выпуклости сплайна в начальной и конечной точках или коэффициент выпуклости и коэффициент асимметрии сплайна;

• ^•    метка (типовой рисунок, используемый для обозначения конструкционных элементов, не имеющих параметрической привязки, например надсечки, петли и др.): m = m(x,y,t), где x, y — координаты, а t — тип метки;

• •    текст: m = m(x, y, ф, "текст"), где x, у, ф — координаты точки привязки и угол наклона "текста".

Учитывая специфику работы проектировщика лекал, каждый примитив можно рассматривать, как класс, а построенный экземпляр примитива — как объект. При таком подходе у каждого объекта должен быть уникальный идентификатор. Это позволит безошибочно находить нужные объекты и обращаться к ним. Таким образом, у каждого примитива должен быть ещё один параметр — текстовая метка. При использовании открытого графического формата SVG рекомендуется использовать этот приём через атрибут id (см. разд. 5.3 рекомендаций W3 C6 . Многие объекты в процессе конструирования используются как промежуточные для построения других объектов. Поэтому, для каждого объекта должна быть возможность задания флага видимости.

Некоторые из примитивов (дуга, сплайн) имеют нестандартное определение. К тому же для построения смежных объектов в таких примитивах должны производиться дополнительные вычисления: для сплайна — приближённое значение длины; для дуги — координаты центра окружности, длина дуги, углы между касательными в крайних точках и горизонтальной осью. Связано это с технологией конструирования, которая представляет собой цепочку операций вычисления очередной точки и связывания точек различными линиями (отрезком, дугой, сплайном). Для вычисления точек необходимо ввести набор соответствующих операций. Приведём минимальный набор таких операций:

• ^•    величина угла между горизонтальной осью и отрезком, образованным двумя точками (p _i , p ₂ ): ф = ф(р 1 ,р 2 );

• ^•    расстояние между точками:

d = d(pi,p2) = V(x2 - xi)2 + (y2 - yi)2/s, где s — параметр масштаба;

• ^•    отложить точку на луче:

p = p(po,ф,d) = {xo + ds соа(ф),уо + ds sin(ф)}, где po(xo,yo) — начало луча, ф — угол между горизонтальной осью и лучом, d — расстояние от начала луча, на котором откладывается новая точка p, а s — параметр масштаба;

• ^•    отложить точку на дуге (с двумя дугами на выходе):

{p, ai, a2} = p(a0, d) = {xo + rs cos^oi — n/4 + d/r), yo + rs sin(фo1 — n/4 + d/r),ai,a2} , где d — расстояние от начала дуги, на котором откладывается новая точка p, a0 , r и φ — исходная дуга, её радиус и угол между горизонтальной осью и касательной к первой точке дуги, соответственно;

• ^•    отложить точку на сплайне (с двумя сплайнами на выходе):

{p, bi,b2} = p(bo,d) = {xi,yi, bi,b2}, где b0 — исходный сплайн, d — расстояние от начала сплайна, на котором откладывается новая точка p(xi,yi), её координаты не могут быть представлены аналитически, они вычисляются приближённо итерационными методами;

• ^•    пересечение прямых:

p = P⁽P 1 ^,Ф 1 ^,P 2 ^,Ф 2 ⁾ =

= {x = (c2 — ci)/(tg ф1 — tg ф2),у = x tg ф1 + ci}, где ci = yi — xi tg фi — свободный член в уравнении прямой;

• ^•    пересечение окружности и прямой (необходимая точка выбирается вручную):

Р = p(p o ,r,Р 1 ,ф) = { x = — u/2 ± V (u/2) ² — v ,y = x tg(ф) + c } , где p o (x o ,y o ) и r — центр и радиус окружности, p i (x i , y i ) и φ — точка на прямой и угол между горизонтальной осью и прямой, c = y 1 — x 1 tg ф — свободный член в уравнении прямой, u = (2ctg ф — 2y o tg ф — 2x o )/(tg ² ф + 1), v = (x o + c ² — 2y o c + У 2 ^— r ² s ^{2 )/(t}g ² ф ⁺ 1);

• ^•    пересечение дуг (окружностей):

Р ± = Р(Р 1 ,Г 1 ,Р 2 ,Ы =

= { x ± = x o + d 2 S cos ф ± ,у ± = y o + d 2 S sin ф ± } , где p i (x i ,y i ) и r i — центр и радиус i-й окружности, ф ± = ф ± п/4, ф = arctg(y 2 — y i )/(x 2 — x i ), d 2 = Vr 2 — d i , x o = x 1 + d 1 s cos ф, y o = y 1 + d 1 s sin ф, d 1 = (r ₁ ² — r ₂ ² + d ² )/(2d), d = V ⁽x i ^— x 2 ^{) 2 + (}y i ^— y 2 ^{) 2 /s};

• ^•    разделение дуги:

^{ P^,a 1 ^,a 2 ^} = Р^(а 0 ⁽Р 01 ^,Р 02 ^,г 0 ^),Р 0 ^,ф⁾ = {^x = ^{— u/2} ± V ^(u/2) 2 ^— v,

),

y = xtg(ф) + c, ai(poi,p, ro), a2(p,po2,ro где ao — исходная дуга, po(xo,yo) и ф — точка на прямой и угол секущей линии, c = yo — xo tg ф — свободный член в уравнении секущей, u = (2c tg ф — 2yoo tg ф — 2xoo)/(tg2 ф + 1), v = (xoo + c2 — 2yooc + y2o — r2s2)/(tg2 ф + 1), ai, a2 — две части исходной дуги;

• ^•    разделение сплайна:

{P,bi ,b2} = Р(b0,Р0,ф0) = {x,y, bi,b2} где bo — исходный сплайн, po(xo,yo) и фo — точка на прямой и угол секущей линии, её координаты и параметры новых сплайнов не могут быть представлены аналитически, они вычисляются приближённо итерационными методами.

В расчётах некоторых параметров графических объектов используется параметр масштаба. Многие параметры графических объектов зависят от размерных признаков, полученных на первом и втором этапах бизнес-процесса (см. рис. 1). Для нахождения некоторых параметров используются нетривиальные методы, а для вычисления параметров, связанных с кривой Безье применяются численные методы.

Согласованность деталей основы на этапе конструирования достигается за счёт автоматического вычисления длин кривых Безье и применением расчётно-графических методик конструирования основы.

Построенная с помощью указанных примитивов и операций основа может использоваться для получения лекал, может быть перестроена при изменении размерных признаков (в результате встроенного в объекты и операции параметрического моделирования) или может подвергнуться дальнейшему моделированию.