Математическое моделирование в управлении персоналом

Существующие прогрессивные математические методы и модели создают новые альтернативы для формализации, инновационного развития и усовершенствования эффективности методов управления персоналом.

В задачах координирования управлением персонала имеется широкий набор математических методов и моделей, к которым можно отнести методы теории игр, математическое моделирование, экспертные модели и технологии. Но при дальнейшем анализе данной статьи будут представлены и рассмотрены модели лишь некоторых типов, которые направлены на повышение эффективности технологий системы управления развитием персоналом. Эта система представляет собой значимую подсистему системы управления персоналом, выступает в роли комплекса организационных структур, технологий, организационно-экономических мероприятий и ресурсов, предназначенных для выполнения задач по обучению, переобучению и повышению квалификации работников организации [1] . Сфера деятельности данной системы охватывает большой спектр задач: оценка кандидатов на вакантную должность, планирование деловой карьеры, работа с кадровым резервом, адаптация персонала в профессиональной деятельности. Достижение наиболее высокой эффективности выполнения перечисленных задач на основе применения математических моделей и методов осуществляется благодаря выявлению новых методик структурирования, обработки и отображения информации об наиболее необходимых вариантах и стратегиях [1] .

Наиболее значимой частью процесса управления организацией является принятие решений. Руководитель, осуществляющий принятие управленческих решений, не может полагаться только на свои собственные навыки, опыт и интуицию, он должен обладать определенными знаниями, владеть методами принятия разумных и правильных решений, навыками общения и работы с людьми. Таким образом, процесс принятия аргументированных и лаконичных решений достигается благодаря использованию математического моделирования в управлении персоналом [3].

Поиск решения задач управления персоналом затрагивает множество факторов, различных по важности, таких как образование психологического климата в коллективе, профессиональный отбор кандидатов и предоставление им должностей, соответствующих уровню их профессиональной подготовки, способностям, интеллекту, умениям и знаниям.

Рассмотрим математическую модель задачи, которая позволяет произвести наиболее выгодное назначение, то есть назначить n-кандидатов на n-свободных должностей, для того чтобы получить наилучший результат от работы группы.

Смысл данной модели задачи сводится к нахождению оптимального значения (max или min) целевой функции

L(X) =^ р₌₁ E y=i c_tj Хи ^ min (max)

при возможных ограничениях:

п

^Xj, = v t^, j=1

L^1 j = 1,n;

t=i

_<      X tj = 0 или 1.

Где X tj = 0, если i-тый кандидат не назначается на j-ую должность, и X tj =1 в противном случае. Элементами c tj матрицы С могут быть время выполнения задания работниками, тогда решается задача на min, полученный доход организации от выполнения поставленных задач и работы, рейтинги кандидатов на должности, тогда решается задача на max.

Таким образом, на конкретном примере, разберем алгоритм решения задачи. Существует пять кандидатов (К 1 , К₂, К₃, К 4 , К ₅ ), претендующих на соответствующие должности ( М 1, М 2 , М₃ , М₄, М 5 ). Для каждого из кандидатов по методике профессиональных предпочтений Дж. Голланда [з] рассчитан рейтинг, данная методика позволяет сопоставить способности, профессиональные качества, уровень интеллекта, предпочтения человека с той или иной областью профессиональной деятельностью. Основная суть данной теории заключается в том, что процветающая профессиональная деятельность во многом зависит от работника, от рабочего климата, способствующего раскрытию способностей человека и повышению желания взаимодействовать с коллективом с максимальной эффективностью. Используя опросник профессиональных предпочтений Дж. Голланда [4] , была сформирована матрица С рейтингов кандидатов на должности по принадлежности и максимальной полезности выполнения определенного типа работы, соотносительно с типом направленности личности. Строки матрицы - претендующие на должности, столбцы матрицы - сами должности. Условие задачи сводится к тому, чтобы назначить на должности кандидатов, тем обеспечив наиболее эффективный профессиональный рейтинг команды. Применим венгерский метод для решения задачи о назначениях кандидатов на должности [5] .

Совершим преобразование матрицы С,

(7 6 6 87\

5  9  7  6  8]

6 8 10 41о|

8 9  9 35

5  7  8 8 7/

Далее произведем умножение всех элементов матрицы на (-1) и сложим каждый элемент полученной матрицы с положительным числом (в данном случае это число 11), так чтобы новая полученная матрица имела только неотрицательные элементы. Имеем следующий вид преобразованной матрицы С:

⎛4 5 5 34

6 2 4 53

5  3  1 7 1⎟

3 2 2 86

6 4 3 34⎠

Произведем вычитание соответствующего минимального элемента из каждой строки и столбца полученной матрицы, для того чтобы получить наибольшее количество нулевых элементов в матрице С. Значения наименьших элементов строк матрицы равны 3,2,1,2,3 соответственно.

Вычитая соответствующее минимальное значение из элементов каждой строки матрицы, получаем следующий ее вид:

1 2 2

0 1

3 1

6 0

6 4

0 1

⎛4 0 2

С = ⎜ 4 2 0

1 0 0

⎝3 1 0

Значения минимальных элементов столбцов матрицы равны 1, 0, 0, 0, 0

соответственно. Вычитая из элементов каждой строки соответствующее минимальное значение, получим:

⎛03

С = ⎜ 3

⎝02

2 2

0 2

2 0

0 0

1 0

0 1

3 1

6 0

6 4

0 1

Так как ни одно полное назначение не получено, то есть нельзя выбрать в каждой строке и каждом столбце по одному единственному нулевому элементу, то необходимо провести модификацию матрицы, с целью получения допустимого решения. Проводим прямые через отдельные строки и столбцы матрицы, чтобы все нулевые элементы были вычеркнуты. Вычеркиваем 1-ую, 3-ю, 4-ую, 5- ую строки и 2-й столбец, Из оставшихся не вычеркнутыми элементов выбираем минимальный, равный 1.

Вычитаем его из всех не вычеркнутых элементов и, прибавляем ко всем элементам, расположенным на пересечении прямых, получим следующую матрицу. Выбираем по одному единственному нулевому элементу в каждой строке и каждом столбце матрицы:

С

/0 3 2 01

2 0 1 20

⎜3 3 0 60

0 1 0 64

⎝2 2 0 01

Заменим в полученной матрице выбранные элементы единицами, а остальные элементы нулями и запишем оптимальное назначение:

У опт

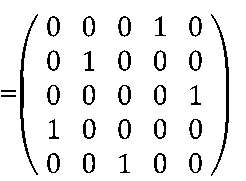
/0 0 0 1 0

0 1 0 0 0

⎜0 0 0 0 1

1 0 0 0 0

⎝0 0 1 0 0

Таким образом, кандидат К1 назначается на должность М4, К2 назначается на должность М2, К3 – на М5, К4 – на М1, К5 – на М3. Суммарный рейтинг всей команды составляет 8+9+10+8+8 = 43. Используя венгерский алгоритм решения задачи о назначении, найден оптимальный вариант по подбору персонала на вакантные должности.