Математическое моделирование вакуумной сублимационной сушки для трансфера технологий с лабораторного уровня на промышленный

В соответствии с прогнозом о научнотехнологическом развитии России до 2030 года, разработка технологий получения готовых лекарственных форм (ГЛФ), а также новых композиционных и дисперсных полимерных материалов является актуальным и приоритетным направлением развития фармацевтики, медицины и смежных сфер науки. К такого рода материалам можно отнести лиофилизаты, представляющие твердую лекарственную форму в виде пористой матрицы с добавлением одного или нескольких действующих веществ [1–7]. Конечной стадией получения готовых лиофилизатов является вакуумная сублимационная сушка, которая часто используется в фармацевтической промышленности для удаления влаги из объема материала с сохранением его исходной формы, без потери структурной целостности и биологической активности препаратов [8]. Однако, ограниченная скорость тепло- и массопереноса, ввиду протекания сублимационной сушки в условиях пониженных температур, обычно приводит к длительному времени сушки и низкой производительности процесса в целом [9]. Продолжительность сублимационной сушки может составлять 24 часа и более. Кроме того, процесс является энерго-и ресурсозатратным, а использование дополнительного оборудования, необходимого для осуществления процесса вакуумной сублимационной сушки, такого как: вакуумный насос, компрессорные установки и холодильная техника, ведет к удорожанию технологии и конечного продукта, поэтому интенсификация данного процесса является актуальной задачей на сегодняшний день [10,11]. Помимо сокращения временных затрат на реализацию процесса, необходимо также гарантировать одинаковую глубину обезвоживания высушиваемых объектов для обеспечения однородности получаемой партии. Партии, не отвечающие установленным фармакопеей требованиям, бракуются. По данным [12] брак в фармацевтической технологии при производстве ГЛФ может составлять до 30 % от общего объема партии, что существенно сказывается на стоимости производства лекарственных препаратов. Поэтому подбор оптимальных режимов сушки в фармацевтической технологии особенно важен.

В области исследования и интенсификации процессов сушки широко применяются методы математического моделирования [13,14]. Данные методы позволяют заменить реальный физический объект на математическое описание данного объекта, с целью его исследования.

Поэтому использование методов математического моделирования в области исследования и интенсификации вакуумной сублимационной сушки позволяет не только рассчитать и подобрать режим сушки, но и существенно сократить материальные, энергетические и временные затраты на эксперимент [15,16]. А использование методов вычислительной гидродинамики позволяет рассчитать распределение водяных паров в объеме рабочей камеры лиофилизатора, что особенно важно для оценки влияния параметров процесса на однородность партии.

В данной работе проводилось математическое моделирование процесса вакуумной сублимационной сушки с учетом неравномерного распределения водяных паров по объему рабочей камеры лиофилизатора. В качестве объекта исследования было выбрано модельное вещество (пептид).

Материалы и методы

В работе были использованы следующие материалы: модельное вещество (пептид), сахароза, L-гистидин, L-гистидина гидрохлорида моногидрат, хлористоводородная кислота 1 М до pH 6.5, полисорбат-80.

Приготовленный раствор на основе модельного и вспомогательных веществ разливали на металлический поддон. Толщина слоя заливки составила 1.5 см. Для проведения процесса вакуумной сублимационной сушки использовалась пилотная установка Labconco (США), поддерживающая возможность заморозки образцов внутри рабочей камеры (рисунок 1).

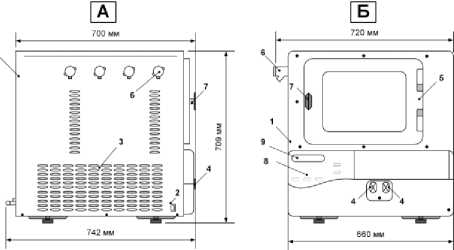
Рисунок 1. а) Схема установки Labconco, вид сбоку: 1 – корпус установки, 2 – кнопка питания, 3 – область конденсатора водяных паров, 4 – вакуумный клапан; б) вид спереди: 5 – дверца рабочей камеры, 6 – вентиляционное отверстие, 7 – ручка дверцы, 8 – панель управления, 9 – дисплей

Figure 1. a) Labconco setup diagram, side view: 1 – setup body, 2 – power button, 3 – water vapor condenser area, 4 – vacuum valve; b) front view: 5 – working chamber door, 6 – ventilation opening, 7 – door handle, 8 – control panel, 9 – display

Экспериментальная работа была проведена в подразделении консультационно-диагностического центра МНИИЭМ им. Г.Н. Габричевского.

Важными технологическими характеристиками пилотной установки Labconco являются: минимальное рабочее давление в камере, равное 5–10 Па и температура конденсатора равная 188 K. Сушильная камера содержит одну нагревательную полку, с диапазоном рабочих температур от 218.15 K до 323.15 K. Емкость конденсатора водяных паров составляет 2.5 л.

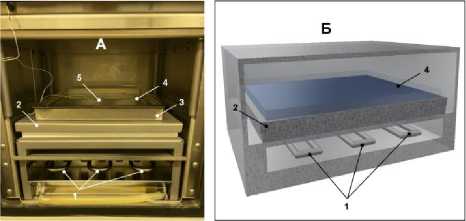
Рисунок 2. а) Внутреннее устройство рабочей камеры установки Labconco: 1 – змеевик конденсатора водяных паров, 2 – нагревательная полка, 3 – поддон, 4 – образец, 5 – датчик температуры; б) 3D-геометрия установки в разрезе

Figure 2.a) Internal structure of the working chamber of the Labconco setup: 1 – water vapor condenser coil, 2 – heating shelf, 3 – tray, 4 – sample, 5 – temperature sensor; b) 3D sectional geometry of the setup

Технологические и геометрические параметры данного оборудования использовались для построения математической модели процесса сушки и прогнозирования распределения водяных паров в объеме рабочей камеры.

На рисунке 2 представлены внутреннее устройство рабочей камеры установки Labconco и 3D-геометрия установки в разрезе, использующаяся при последующем моделировании потока водяных паров в рабочей камере.

При проведении экспериментальной работы на пилотной установке Labconco сначала предварительно охлаждали область конденсатора (1) и нагревательную полку (2). Затем заранее приготовленный раствор объемом 1 л равномерно распределяли по поддону (3). Поддон (3) вместе с образцом (4) помещали на нагревательную полку (2). В объем образца (4) по центру вводили датчик температуры (5). Рабочая камера закрывалась и на панели управления задавались условия предварительной заморозки образца: температура – 233 K; время выдерживания после достижения заданной температуры – 360 мин, без вакуумирования.

После завершения этапа предварительной заморозки установка в автоматическом режиме переходила к этапу сушки. В таблице 1 приведены температурно-временные параметры процесса сушки с вакуумированием.

Таблица 1.

Температурно-временные параметры сушки на пилотной установке Labconco

Table 1.

Temperature and time parameters of drying on the Labconco pilot plant

T полки , K	263.15	268.15	273.15	283.15	298.15
Скорость нагрева полки, K/мин Shelf heating speed, K/min	0.25	0.25	0.05	0.05	0.15
Время выдерживания, мин Holding time, min	300	300	480	480	780

Для передачи данных о ходе процесса использовался интерфейс RS-232. Данные передавались с установки на персональный компьютер каждые 5 минут и сохранялись в протоколе. Полученные результаты изменения температуры змеевика конденсатора, нагревательной полки и образца во время этапов предварительной заморозки и сублимационной сушки приведены на рисунке 3 а. Для измерения давления в рабочей камере применяется датчик Пирани. Вакуумирование камеры происходит только на этапе сушки, поэтому изменение давления в камере фиксируется в интервале времени от 1390 до 3995 минут, соответствующему этапу сублимации (рисунок 3 б).

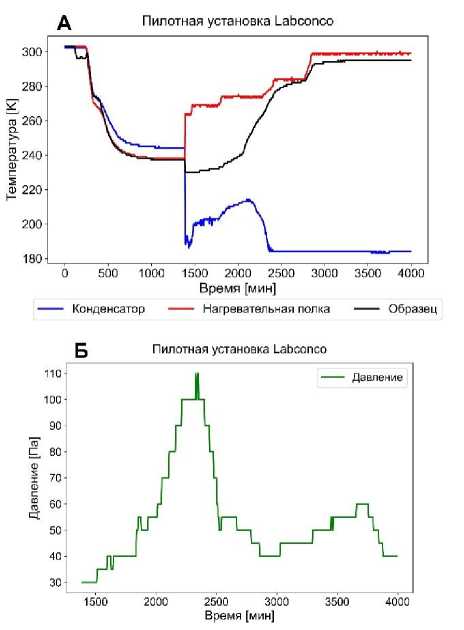
Рисунок 3. а) Экспериментальные данные о ходе процесса сублимационной сушки образца альгината натрия: изменение температуры; б) изменение давления Figure 3. a) Experimental data on the progress of the sublimation drying process of a sodium alginate sample: change in temperature; b) change in pressure

Полученные данные изменения температуры образца использовались для последующей оценки адекватности математической модели кинетики сушки.

Математическое моделирование вакуумной сублимационной сушки

Математическая модель кинетики сушки является одномерной, т. е. перенос тепла и влаги происходит только вдоль оси Х , и строится на уравнениях тепло- и массопереноса. В структуру настоящей математической модели входит описание первого и второго периодов сушки [17].

В математической модели делается допущение об однородности теплофизических параметров замороженного и высушенного слоев материала по объему в каждый момент времени. Значения плотности, удельной теплоемкости и теплопроводности рассматривались как постоянные по всей толщине слоя [18].

В ходе расчета весь материал делился по высоте на 50 слоев, в каждом из которых рассчитывалось изменение влагосодержания и температуры материала во времени [19]. Шаг по времени выбирался из условия устойчивости разностной схемы (условие Куранта).

Перемещение фронта сушки осуществляется послойно: высушенный слой меняет статус с «лед» на «сухой материал».

В данной работе кинетическая модель для высушиваемого материала – код Python, объединялись с CFD-моделью распределения водяных паров по объему пилотного лиофилизатора. Для этого значения изменения температуры и влагосодержания материала, полученные по кинетической модели, записывались в UDF-файлы: temperature_flow и mass_flow_rate. UDF-файлы прикреплялись к соответствующим областям 3D-геометрии сублимационной камеры, в качестве граничных условий в среде моделирования Ansys Fluent 17.0 (рисунок 4).

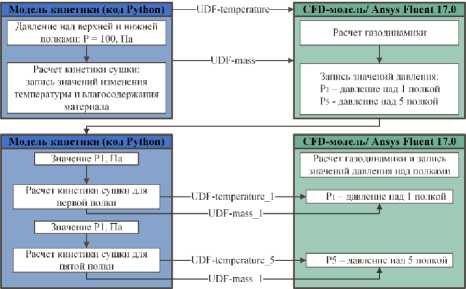
Рисунок 4. Алгоритм объединения двух моделей

Figure 4. Algorithm for combining two models

Такой подход позволил получить модель с учетом неравномерного распределения водяных паров по объему вакуумной камеры.

При составлении математического описания первого периода сушки для условно гомогенного материала, был принят ряд следующих допущений:

• 1.    Весь материал делится на 50 слоев, в каждом из которых рассчитывается изменение влагосодержания и температуры, с учетом особенностей строения материала.

• 2.    Фронт сублимации, положение которого задается координатой X н , делит образец на замороженную область (I) и высушенную (II) области.

• 3.    Граница раздела (фронт сублимации) в процессе сушки равномерно двигается вниз, пока вся замороженная свободная влага не удалится из материала толщиной L . При этом меняется статус слоя: с «лед» на «сухой материал». Высота слоев остается постоянной в течение всего расчета.

• 4.    На границе раздела фаз выполняется закон сохранения массы.

• 5.    Теплопередача к материалу осуществляется кондуктивно от полки снизу.

Для замороженной области (I) уравнение теплопроводности и граничное условие выглядят следующим образом:

д T d ² T Q,

— = aI—Ir + (1) д т d x ² р, c_pJ

0 <  x <  X ( т ) , т> 0 (2) где T – температура, К; τ – время, с; a I – температуропроводность, м²/с; x – декартова координата, м; Q I – объемная мощность источников теплоты, Вт/м³; ρ I – плотность, кг/м³; c pI – удельная теплоемкость, Дж/(кг‧К).

Для высушенной области (II) уравнение теплопроводности и граничное условие выглядят так, как показано ниже:

T „ d T   -  dNT) * Q   m n     aii n 2                 Л      +            (3)

^{дт       д} x     P ii^c _p ii      ^д x        Ри ^c _p ii

X ( т ) < x <  L, т >  0 (4) где ρ II – насыпная плотность сухого материала, кг/м³; N пар – поток водяного пара во II области, кг/(м²‧с).

Дифференциальные уравнения, описывающие массообмен для замороженной области (I) и высушенной области (II) представлены ниже:

Ai ^ =( WH - W P AHc X(5)

X x = Xj, т > 0(6)

Aii T = -( Wh - w„ )p„ AHс X(7)

дX      '           '

X = X;> 0(8)

Приращение координаты и влагосодержа-ния для замороженной области (I) в размерном виде представлено ниже:

dX,     Л    ( ^ТФс ^{- Т}низ )

d r ~X i P ii A H ( W h - W_Kp )

dW_r    ^A i ( ^Тфс ^{- Т}низ )

dт   L ■ A H X_rp_n

где λ – теплопроводность материала, Вт/(м⋅K); W н – начальное влагосодержание, кг влаж-ного/кг сухого материала; W кр – критическое влагосодержание, кг влажного/кг сухого материала; Δ H c – энтальпия сублимации, Дж/кг; Т фс – температура фронта сублимации, К; Т низ – нагревательной полки, К.

Приращение координаты и влагосодержа-ния для замороженной области (I) в безразмерном виде представлено ниже:

dX *       A,      ( ^Тфс ^{- Т}низ )

= (11)

d T   a i ^X i P ii A H с ( W h - W_K p )

dw; _   A i     ( ^Тфс ^{- Т}низ )

^{d T}    a i^Xi P ii A H ( W h - W_K p )

Приращение координаты и влагосодержа-ния для высушенной области (II) в размерном виде представлено ниже:

dX _n _     A_n      ( ^Тфс ^{- Т}ов )

d т “( L - X ii ) P ii A H ( W h - W_K p )

dW_ir       ^A ii ( ^Т фс ^{- Т} пов )

d т L • p _i A H с ( L - X II )

где Т пов – температура поверхности материала, К.

Приращение координаты и влагосодер-жания для высушенной области (II) в безразмерном виде представлено ниже:

dX* _     A_n       (Т ффс Т )

d T     a i J ^{(1 - X} _n ) P ii A H с ( W h - W_K p )

^dWii _       ^A ii ^{( Тфс  Т}пов )     (16)

d T *   a ii ^{(1 - X} * ) P ii AH с ( W h - W_K p )

Приращение координаты фронта сублимации ∆X и влагосодержания ∆W в безразмерном виде рассчитывалось по уравнениям для замороженной и высушенной областей соответственно:

A X n ^{n + 1} =AW: ^{n + 1} = q *^{: n + 1} - Ste_t - A т      (17)

A X * n ^{+ 1} = A W * ^{n + 1} = q *^{: n + 1} • Stej, - A т     (18)

Числа Стефана SteI и SteII рассчитывались по уравнениям, представленным ниже:

A _i     ( ^Тниз ^{- Т}фс )

Stej =

Ste_n =

a i p_n A H с ( W h - W p ) A    ( ^Т„ _О в ^{- Т}фс )

a i ,p_n A H с ( W h - W _K p )

Расчет смещения фронта сублимации X^*n+ ¹ и изменения влагосодержания W^*n+ ¹ проводился также в безразмерном виде по уравнениям:

X *n+1 = X *n + AX*n+1 + AX*n+1

W * n+1 = w * n + AW*n+1 + AW*n+1

Перевод влагосодержания в размерный вид осуществлялся по формуле:

W = W * ( Wh-W^) + Wp(23)

где W – текущее влагосодержание, кг влаж-ного/кг сухого материала.

Начальное условие для замороженной и высушенной областей материала приведено ниже:

T = T,,0 < x < L, т = 0(24)

W = WH ,0 < x < L ,r = 0(25)

Граничные условия для нижней (I) и верхней (II) частей материала представлены ниже:

Тниз = T,, x = 0, т> 0(26)

Tn =, x = L, т > 0(27)

x

В момент времени, когда текущее влаго-содержание материала ( W ) становится равным критическому влагосодержанию ( W кр ) начинается второй период сушки. При составлении математического описания второго периода сушки были сделаны следующие допущения:

• 1.    содержание влаги в материале в момент начала второго периода сушки равно критическому влагосодержанию при средней температуре высушенного слоя в конце этапа сублимации ( W = W кр );

• 2.    механизмом массопереноса является десорбция влаги.

Баланс влаги в высушенной области материала рассчитывался по формуле, приведенной ниже:

Баланс влаги в высушенной области материала рассчитывался по формуле, приведенной ниже:

Для расчета теплового баланса в высушенном слое использовалось следующее уравнение:

i d2 T _л      x      дT         Р кж дW

— ^--T + (1 — Poo I P Cm --+ / A hade --= 0 ⁽³⁵⁾

дx2  \   пороге дт £ адс M° дт где ∆hадс – теплота адсорбции, Дж/моль.

Начальные условия для решения уравнений второго периода сушки:

W = Wkp , т = 0

T = T ( x ,0 ) , r = 0

Граничные условия для решения уравне-

d W = K ( W„ - W )

дт

где W экв – эквивалентное влагосодержание, кг влажного/кг сухого материала.

Для расчета кинетического коэффициента K использовалось уравнение:

60D эфф d2 пор

где D эфф – коэффициент эффективной диффузии, м²/с; d пор – диаметр пор, м.

Эффективный коэффициент диффузии D эфф , а также коэффициент диффузии по Кнудсену D K и коэффициент поверхностной диффузии D пов рассчитывались по следующим формулам:

£ M ду ’ пор в  yпар

^Dэфф = D noe + ^DK

p д W

D k = 1.0638 r _nop

D noB = D o 0 exp

где ε пор – пористость; М в – молекулярная масса воды, г/моль; r пор –радиус пор, м; E а – энергия активации, Дж/моль; R – универсальная газовая постоянная, Дж/(мольK).

Производная д y * /д W в уравнении (31)

рассчитывалась аналитически:

д y * y пар

CW

P W — W _o exp I | I

где y пар – равновесная мольная доля водяного пара, моль / моль; a – константа, K; b – константа, Па^-1; c – константа, K; P-давление, Па.

ний второго периода сушки:

T = Т из , x = 0, r >  0

d T

— = 0, x = L, т> 0 дx

Для реализации расчетов

кинетики

сушки вышеописанная математическая модель была оформлена в программный код на языке программирования Python.

Для оценки сопоставимости кинетических кривых сушки использовались факторы различия и подобия. Фактор различия ( f 1 ) показывает процент ошибки между двумя кривыми сушки, полученными при разных режимах, по всем временным точкам. Фактор различия рассчитывается по уравнению (40):

/1 =

k t=1   skcnt      pac4emt

k

L-i t = 1 ^эксп 1

100 %    (40)

где T – экспериментальная средняя температура в момент времени τ , K; T – эрасчет-ная средняя температура материала в момент времени τ , K.

Фактор различия равен нулю, если кривые сушки идентичны. По мере увеличения различия между двумя кривыми сушки значение фактора возрастает. Кинетические кривые сушки считаются сопоставимыми, если значение фактора различия f 1 находится в интервале от 0 до 15.

Фактор подобия ( f 2 ) – это величина, представляющая собой логарифмическое преобразование значения суммы квадратов ошибок, рассчитанных по разности между значениями двух кривых сушки во всех точках времени. Фактор подобия рассчитывается по уравнению (41):

f = 50 log 100

k

' t = 1

T -T экспt      расчетt

k

где k – количество временных точек.

Кинетические кривые сушки считаются сопоставимыми, если значение фактора подобия f 2 находится в интервале от 50 до 100.

Если хотя бы один из факторов не попадает в диапазон значений, при которых кинетические кривые считаются сопоставимыми, то принимают, что такие кривые значимо различаются.

На основании полученных данных кинетики сублимационной сушки с помощью метода вычислительной гидродинамики (CFD) и пакета программ Ansys Fluent 17.0 были произведены расчеты распределения водяных паров в объеме рабочей камеры пилотной установки Labconco.

Результаты и обсуждение

Анализ графиков температуры (рисунок 3 а) показал, что, начиная с 255 минут, система начинает активно охлаждаться (резкое падение температуры нагревательной полки, конденсатора и образца). В период времени от 330 до 405 минут наблюдается температурное плато, соответствующее фазовому переходу на этапе заморозки. Период времени от 405 до 1390 минут соответствует полному затвердеванию раствора. Начиная от 1390 минут, установка переходит к этапу сушки. В данный момент времени давление в рабочей камере снижается от нормально атмосферного давления до уровня вакуума, равного 30 Па (рисунок 3 б). Вакуумирование рабочей камеры приводит к резкому понижению температуры конденсатора, а понижение температуры образца связано с эффектом само-замораживания. Температура нагревательной полки повышается в соответствии с заданным режимом (таблица 2). В интервале времени от 1390 до 2180 минут протекает первый период сушки (сублимация льда). Конденсатор активно поглощает водяные пары, поступающие из рабочей зоны, соответственно температура конденсатора (рисунок 3 а) и давление в рабочей камере (рисунок 3 б) повышаются. Пик температуры конденсатора и пик давления в рабочей камере соответствуют завершению первого периода сушки. Начиная с 2180 минут образец начинает активно прогреваться (начало второго периода сушки), температура образца повышается до заданной температуры нагревательной полки (досушка образца при положительных температурах). Во втором периоде сушки лимитирует диффузионный перенос влаги и скорость сушки падает, следовательно, нагрузка на конденсатор снижается, что приводит к уменьшению температуры конденсатора. Концентрация водяных паров в рабочей камере также снижается, что приводит к уменьшению давления.

Результаты оценки адекватности математической модели кинетики вакуумной сублимационной сушки приведены на рисунке 5.

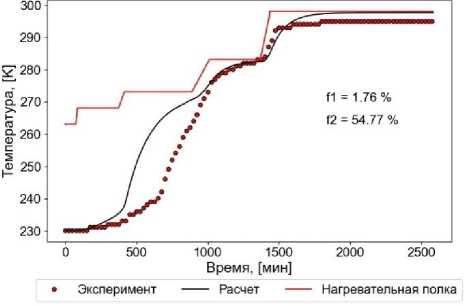
Рисунок 5.Оценка адекватности математической модели кинетики вакуумной сублимационной сушки образца

Figure 5. Evaluation of the adequacy of the mathematical model of the kinetics of vacuum sublimation drying of a sample

Рассчитанные значения факторов различия f 1 – 1.76, и подобия f 2 – 54.77, позволили оценить адекватность математической модели кинетики вакуумной сублимационной сушки. Ни один из факторов не выходит за диапазон значений, при которых кинетические кривые значимо различаются. Следовательно, температурные кривые являются сопоставимыми, а математическая модель адекватно описывает экспериментальные данные.

На рисунке 6 приведено распределение доли водяного пара в объеме рабочей камеры (вид сбоку) в интервале времени от 33 до 333 минут.

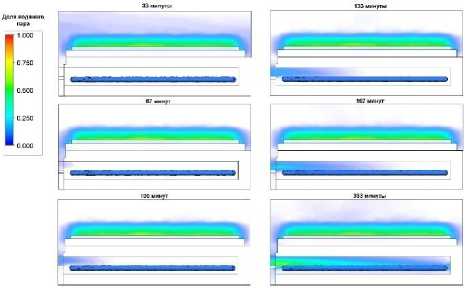
Рисунок 6. Распределение доли водяного пара в объеме рабочей камеры пилотной установки Labconco (вид сбоку)

Figure 6. Distribution of the proportion of water vapor in the volume of the working chamber of the Labconco pilot plant (side view)

В момент времени 33 минуты водяной пар в основном сосредоточен в верхней части рабочей камеры (область материала). Под действием разности парциальных давлений, водяной пар постепенно двигается в область конденсатора водяных паров. К моменту времени, равному 333 минуты, доля водяного пара в области конденсатора значительно увеличивается.

Мохова Е.К.и др.Вестник ВГУИТ, 2025, Т. 87, №. 3, С. 224-233 Полученные данные согласуются с экспериментальными – Рис. 3 А, где в момент времени 1723 минуты (333 минуты от начала процесса сублимационной сушки) видно, что нагрузка на конденсатор повышается, а его температура возрастает.

Заключение

Разработанный подход математического моделирования, основанный на объединении модели кинетики сушки (код – язык программирования Python) и CFD-моделирования газодинамики (программный пакет Ansys Fluent 17.0) для материалов, представляющих интерес для фармацевтической промышленности, является эффективным в области исследования и подбора режимов вакуумной сублимационной сушки в аппаратах различного объема.

Стоит отметить, что разработанная математическая модель позволяет подбирать технологические режимы ведения процесса для различных типов материалов, что существенно сокращает материальные и энергетические затраты, а также время на эксперимент.

Совместное использование математической модели кинетики сушки и CFD-моделирования газодинамики показало, что рассчитываемые данные согласуются с экспериментальными, поэтому данный подход может быть предложен при осуществлении трансфера технологии с лабораторного уровня на промышленный.

Работа выполнена в рамках государственного задания (проект FSSM-2025–0003).