Математическое моделирование вестибулярного нистагма. Часть I. Статистическая модель
Автор: Боков Т.Ю., Сучалкина А.Ф., Якушева Е.В., Якушев А.Г.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 1 (63) т.18, 2014 года.
Бесплатный доступ
Цель работы - на основе анализа экспериментальных данных построить математическую модель нистагма, воспроизводящую его статистические характеристики. Экспериментальное изучение нистагма проводилось в лабораторных условиях на вестибулярном кресле. Специально подобранное визульное окружение создавало оптокинетическую стимуляцию. Движения глаз регистрировались с помощью метода электроокулографии. Экспериментальные траектории нистагма демонстрируют существенную вариабельность. По типичным нистагменным кривым выбраны пять параметров, которые характеризуют медленную фазу нистагменного цикла. По результатам обработки записей нистагма, полученным при обследовании добровольцев, построены гистограммы этих параметров. Проверено, что один из параметров, амплитуда угла поворота глаза на протяжении медленной фазы, имеет нормальное распределение, тогда как распределения остальных параметров существенно отличаются от нормального, поэтому для их моделирования применен метод обратного преобразования. В работе предложена статистическая модель вестибулярного нистагма. Эта модель по заданному закону вращения головы формирует циклически чередующуюся последовательность медленных и быстрых фаз нистагма, возникающего при таком вращении головы, с учетом наличия или отсутствия визуальной стимуляции. С помощью статистической модели построены серии модельных траекторий глаз для двух видов нистагма - оптокинето-вестибуло-цервикального и вестибулярного. Для проверки модели с помощью критерия Пирсона проведено сравнение распределений параметров модельных траекторий нистагма с экспериментальными распределениями тех же параметров, полученными по записям, сделанными при такой же комбинации зрительных, вестибулярных и проприоцептивных стимулов. В результате сравнения установлено хорошее статистическое соответствие модельной и экспериментальной траекторий.
Вестибулярный нистагм, статистический метод, ранговый критерий спирмена, критерий пирсона, преобразование бокса-мюллера, метод обратного преобразования
Короткий адрес: https://sciup.org/146216124
IDR: 146216124 | УДК: 57.087.1
Текст научной статьи Математическое моделирование вестибулярного нистагма. Часть I. Статистическая модель
Нистагм представляет собой серию непроизвольных ритмичных содружественных движений глаз. Различают две фазы нистагма: медленное отклонение глаза в одном направлении и сменяющий его быстрый возвратный скачок. Вестибулярный нистагм может быть вызван ускоренным движением, тепловой
Якушев Андрей Германович, к.ф.-м.н., c.н.с. кафедры прикладной механики и управления, Москва стимуляцией полукружных каналов, электрической стимуляцией вестибулярного нерва, механическим воздействием на перепончатый лабиринт, а в некоторых случаях его появление может быть связано с центральной или периферической вестибулярной патологией [10].
В зависимости от сочетания действующих стимулов выделяют несколько видов вестибулярного нистагма, отличающихся комбинациями шейной проприоцептивной или оптокинетической стимуляции [8]. Одна из классификаций видов нистагма приведена в табл. 1.
Существует множество различных взглядов на происхождение вестибулярного нистагма и на то, какую он играет роль. Корюкин считает, что вестибулярный нистагм не является оправданной реакцией [11]. Филин считает, что неблагоприятные факторы: механическое сдавливание опухолью структур саккадического центра, космические перегрузки, укачивание, интоксикация (алкогольная, наркотическая, токсическая) – нарушают привычный режим работы саккадического центра, в результате чего появляются выраженные колебания глаз, известные в клинической практике как нистагм. Филин делает вывод, что нистагм – это нарушение автоматии саккад [12]. Бабияк пишет: «…экспериментально вызванный нистагм (в норме) следует признать “запредельной” реакцией, обусловленной действием неадекватного раздражителя (пусть даже специфического). В биологическом отношении нистагм не является необходимой реакцией, поскольку в процессе эволюции не существовало условий, требующих для нормальной жизнедеятельности организма этой реакции» [3].
Особый интерес вызывает точка зрения Митькина: «Филогенетическое развитие моторики глаз протекало в условиях взаимодействия вестибулярной и ретинальной афферентации. Нетрудно понять, что изолированное самодовлеющее влияние лабиринтных рецепторов на глазодвигательные мышцы превратилось бы в биологическую бессмыслицу. Напротив, тончайшая корреляция между лабиринтными и сеточными афферентными сигналами и создает “чудо” в моторике глаз, о котором говорит Гранит. Взаимосвязь медленной и быстрой фаз нистагма носит характер базового, генетически закрепленного автоматизма стволового уровня» [9].
Ситуации, в которых наблюдается вестибулярный нистагм, часто сопровождаются возникновением сенсорного конфликта. Характеристика сенсорных конфликтов, возникающих в условиях движения головы или тела человека, предложена Сучалкиной [15].
В литературе можно найти сравнительно немного моделей вестибулярного нистагма. Некоторые из этих моделей описаны ниже. Однако все они носят детерминированный характер.
Таблица 1
Характеристика видов нистагма по сенсорным входам
|
Оптокинетическая стимуляция Шейная проприоцептивная стимуляция |
Глаза закрыты |
Глаза открыты |
|
Пассивные вращения головы |
Вестибулярный нистагм |
Оптокинето-вестибулярный нистагм |
|
Активные вращения головы |
Вестибуло-цервикальный нистагм |
Оптокинето-вестибуло-цервикальный нистагм |
В данной работе впервые ставится вопрос о статистическом изучении и моделировании вестибулярного нистагма. В эксперименте обнаруживается, что нистагменные движения глаз человека сильно вариабельны, траектории нистагма не совпадают при повторных испытаниях даже у одного и того же испытуемого, получаемые записи визуально существенно отличаются друг от друга. По этой причине невозможно говорить о непосредственном сравнении траектории нистагма (например, наложением). Как будет показано в работе, эмпирические распределения практически всех параметров нистагма существенно отличаются от нормального. Поэтому сравнение характеристик, описывающих траектории нистагма, по их средним значениям и дисперсиям представляется недостаточным, так как эти параметры являются исчерпывающими только для нормального распределения.
В данной работе описана статистическая модель вестибулярного нистагма, вырабатывающая модельные траектории нистагма, имеющие статистические характеристики, соответствующие наблюдаемым в эксперименте.
Предыдущие модели нистагма
Для описания моделей нистагма введем условные обозначения. Обозначим геометрический центр головы за O , геометрический центр глаза – за O 1 . Свяжем неподвижную систему отсчета Oxyz с абсолютным пространством: ось Ox лежит в коронарной плоскости, ось Oy лежит в сагиттальной плоскости, оси Ox и Oy параллельны трансверсальной плоскости, а ось Oz дополняет Ox и Oy до правой тройки. Угол поворота головы вокруг оси Oz в системе Oxyz обозначим за θ. Подвижная система отсчета Ox'y'z' связана с головой: ось Ox' направлена в сторону правого уха, ось Oz' совпадает с осью Oz неподвижной системы координат, а ось Oy' дополняет Ox' и Oz' до правой тройки. Угол поворота глаза вокруг оси O 1 z' в системе Ox'y'z' обозначим за φ. Будем разделять φ S ( t ) и φ F ( t ) – зависимости угла поворота глаза от времени в течение медленной и быстрой фаз нистагма соответственно. Подвижная и неподвижная системы отсчета изображены на рис. 1 (вид сверху, l – линия взора).
Также введем обозначения для моментов времени и амплитуд. Абсолютное время обозначается за t , относительное время, прошедшее с начала текущей медленной фазы, за τ, длительности медленной и быстрой фаз – за T S и T F , моменты начала
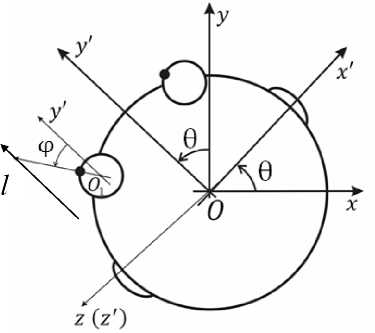
Рис. 1. Системы отсчета и углы поворота
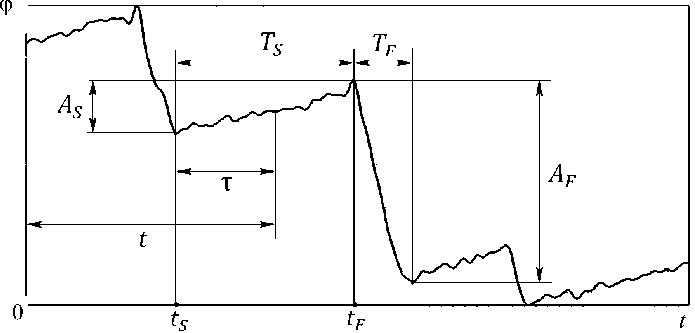
Рис. 2. Обозначение промежутков времени и амплитуд медленной и быстрой фаз – tS и tF, амплитуды медленной и быстрой фаз – за AS и AF соответственно. Обозначения показаны на рис. 2. В дальнейшем используется время τ , если не оговорено иное. Для амплитуд медленной фазы головы и глаза при необходимости будут использоваться обозначения AH и AE соответственно.
Одной из первых математических моделей вестибулярного нистагма можно считать модель Шмида 1970 г. [20]. Эта одномерная эмпирическая модель описывает вестибулярный нистагм в горизонтальной плоскости, возникающий при вращении испытуемого по синусоидальному закону вокруг вертикальной оси в темноте. Рассматриваются пассивные движения головы. Модель учитывает непостоянные амплитуды ударов нистагма и продолжительности медленных компонентов нистагма.
В 2002 г. Шмид и соавторы предложили модернизированную математическую модель нистагма [19]. Ключевая гипотеза модели заключается в том, что информация о движении головы передается в саккадический механизм через сложный вестибуло-саккадический путь, состоящий из двух ветвей, т.е. финальная позиция глаза зависит как от сигнала о положении головы, так и от сигнала об угловой скорости движения головы. Данная модель описывает возникновение вращательного нистагма в горизонтальной плоскости в темноте.
В 2001 г. Мерфельд и соавторы представили модель, описывающую компенсаторные движения глаз во время проявления вестибуло-окулярного рефлекса (т.е. медленный компонент нистагма) [17]. При построении модели они использовали весовую модель оценивания сигналов центральной нервной системой.
В работе Сучалкиной [7] медленная фаза моделируется с помощью уравнений Голдберга–Фернандеса [18], а для определения моментов смены фаз используются два импульсных генератора.
Модель, предложенная в работе Штефановой [13], основана на определении параметров очередной медленной (быстрой) фазы по значениям параметров в конце предыдущей быстрой (медленной) фазы. В этой модели угловая амплитуда медленной фазы ASi полагается зависимой от φ(0) :
A S ( ф(0) ) = o f ( Ф(О) ) 3 + a 2 ( ф(0) ) 2 + a 3 ( ф(0) ) + a 4 , (1)
где индекс i обозначает вид нистагма - оптокинето-вестибуло-цервикальный ( i = 1), оптокинето-вестибулярный ( i = 2 ), вестибуло-цервикальный ( i = 3) или вестибулярный ( I = 4).
Относительный угол поворота глаза φ(τ) моделируется как линейная функция угла поворота головы:
Ф(т) = Ф(0) + Ki (6(т)-6(0))•
Здесь K i – коэффициент усиления, зависящий от наличия оптической стимуляции, для оптокинетических видов нистагма K 1 = K 2 = - 1, а в случае вращения в темноте K 1 = K 2 = - 0,83. Кроме того, для оптокинето-вестибуло-цервикального и оптокинето-вестибулярного видов к φ(τ) прибавляется функция вида
Фmis (Т) = cmissign (9 (Т)) Л где cmis = 18° / с2. Это слагаемое необходимо в силу того, что, судя по экспериментальным записям, положение глаза в конечный момент не всегда совпадает с получаемым по формуле (1). Зная амплитуду медленной фазы и типичную форму траектории глаза, можно полностью определить закон движения глаза.
Для быстрой фазы амплитуда A F полагается зависимой от 9 ( T S ) и ф ( T S ) по следующему закону:
AF = к99 ( Ts )-ф ( Ts ).
Здесь k θ i – коэффициент усиления: для оптокинето-вестибуло-цервикального и оптокинето-вестибулярного видов к 11 = к д = 0,475 с, а для вестибуло-цервикального и вестибулярного типов к 1 = к д = 0,228 с. Коэффициент для оптокинетических видов больше, что отражает тот факт, что амплитуда саккады при открытых глазах больше.
Средняя угловая скорость глаза tol F во время быстрой фазы полагается связанной с амплитудой быстрой фазы AFi :
™ F = b,( AF) \ где bi и qi – постоянные величины, различные для каждого вида нистагма.
Длительность быстрой фазы TFi можно рассчитать по формуле
T F = - F . ω i F
Из опытных данных известно, что максимальной угловой скорости глаз достигает в середине саккады, поэтому φ(τ) во время быстрой фазы изменяется по закону
Ai
1 -
cos (т - T S )
T
.
Ф ( т ) = Ф ( Ts ) + "у
Экспериментальное изучение нистагма
Изучение нистагма проводилось на базе детской психоневрологической больницы № 18 г. Москвы. Аппаратная часть включала в себя:
-
1) электровращательное кресло RS -6 компании Servomed , Швеция;
-
2) cистему «Окулостим», состоящую из электронистагмографа и программного обеспечения (программы «Нистагм») производства НМФ «Статокин», Россия;
-
3) датчик угловой скорости головы;
-
4) светодиодный экран на основе модуля Ke-USB 24 R фирмы Kernelchip для проведения калибровки и моделирования саккад;
-
5) штору с неярким однородным рисунком для создания однородной оптокинетической стимуляции при вращении головы.
Исследовались следующие виды нистагма: оптокинето-вестибуло- цервикальный, вестибуло-цервикальный, оптокинето-вестибулярный и вестибулярный.
Во всех случаях испытуемому давалось задание смотреть прямо перед собой, не отслеживая какую-то конкретную цель; вращение головы носило синусоидальный характер с амплитудой 60° и периодом 8 с. В случае оптокинетических видов эксперимент происходил в освещенном помещении, в случае неоптокинетических – в темноте; в случае цервикальных видов испытуемый активно вращал головой, в случае нецервикальных – кресло совершало вращение, вызывая пассивные движения головы.
Регистрация движений глаз проводилась с помощью электронистагмографа. Измерялись горизонтальные движения глаз, поэтому многоразовые электроды прикреплялись следующим образом: два в углах глаз (в височной области) и один за ухом (в области сосцевидного отростка височной кости). При помощи программы «Нистагм» были получены записи трех параметров: абсолютного времени t , абсолютной угловой скорости головы ω H и относительного угла поворота глаза φ.
Обработка результатов обследований
Для анализа нистагменных циклов было взято по 20 фрагментов записей опто-вестибуло-цервикального и вестибулярного нистагмов длительностью от 30 до 60 с. Для этих записей для каждого вида нистагма были вычислены значения шести параметров – модуля угловой скорости глаза ω E в момент окончания медленной фазы, модулей амплитуд поворота головы A H и глаза A E на протяжении медленной фазы, длительности медленной T S и быстрой T F фаз, а также величины γ , условно названной «удельной работой мышц глаза» и определяемой по формуле
T S
Y =
A E T S
J ( ф (т) - ф (0) ) d T
Медленные фазы были разделены на две группы: 1) те, во время которых абсолютная угловая скорость головы ω H не меняет знака; 2) те, во время которых ω H меняет знак.
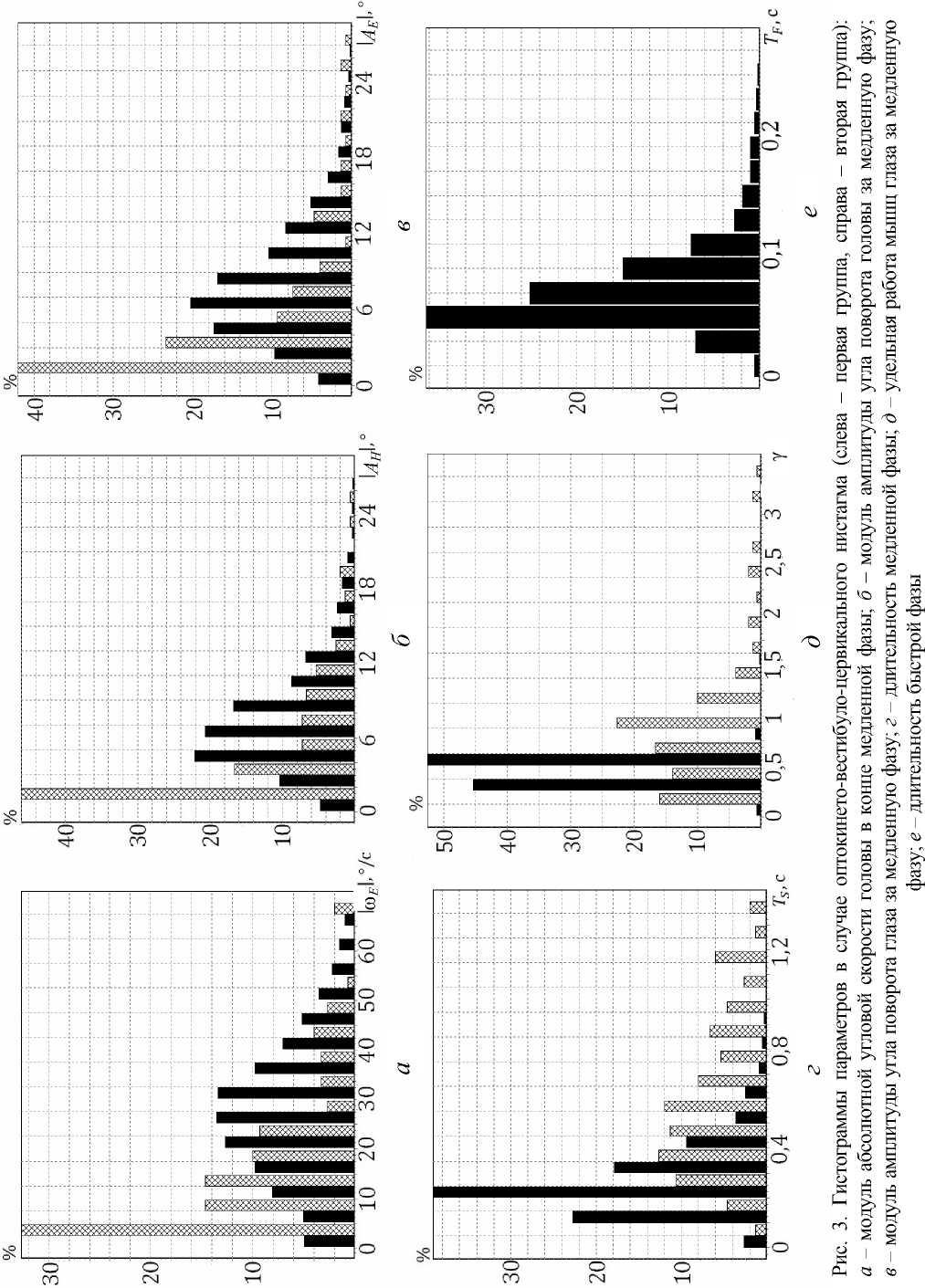
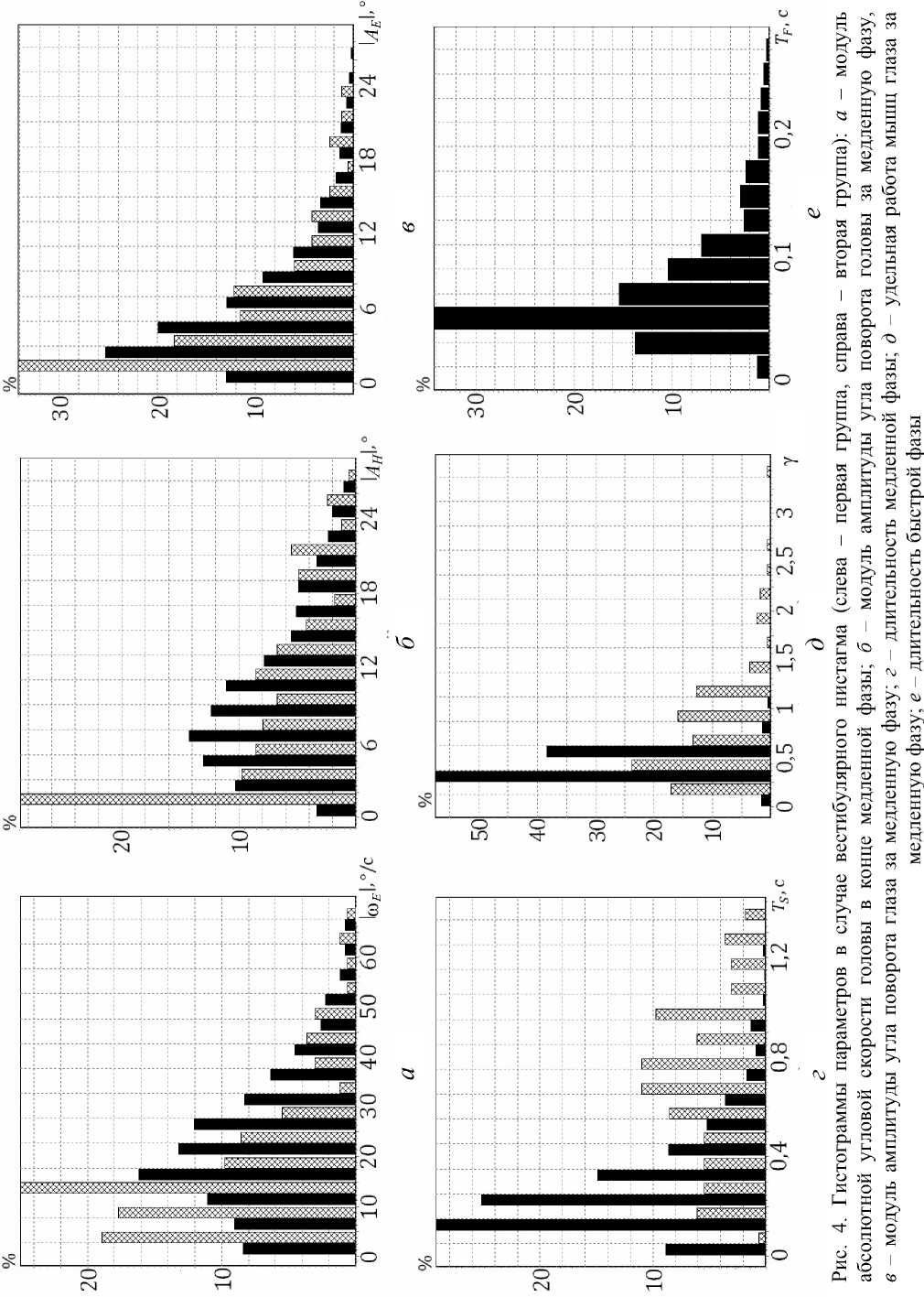
Поскольку все записи в сумме содержат около 1500 медленных фаз, в соответствии с рекомендациями, приведенными в работе [4], было принято, что количество разрядов гистограмм K будет равняться 14. Полученные гистограммы параметров для случаев оптокинето-вестибуло-цервикального и вестибулярного нистагмов для двух групп медленных фаз показаны на рис. 3 и 4 соответственно.
Проверка распределений на нормальность
Для гистограмм, показанных на рис. 3 и 4, была проведена проверка гипотезы о соответствии распределения каждого из шести параметров усеченному нормальному распределению. В качестве ожидаемых плотностей распределения были выбраны приближения эмпирических распределений законом
p ( x ) =
C
2 exp 2πσ2
( x - Ц ) 2 2o2
x > 0,
где µ – математическое ожидание; σ2 – дисперсия; константа C определяется из условия
Jp (x) dx = 1,
т.е.
C = 72no 2
c o
J exp
(x - ц)
2σ2
dx
- 1
Параметр µ был принят равным выборочному среднему, а параметр σ2 был принят равным исправленной выборочной дисперсии [1]. Параметры аппроксимации распределений для медленных фаз первой и второй группы приведены в табл. 2 и 3.
Для проверки гипотезы о нормальности распределения использован критерий согласия Пирсона [4], позволяющий проверить согласованность наблюдаемого распределения частот с ожидаемым распределением частот. Суть критерия состоит в том, что, если выделены K разрядов и известны {f i } и { F i }, i = 1... K , соответственно наблюдаемое и ожидаемое распределения частот, то величина X 2, определяемая по формуле
, -FV
X 2 =y (Л ij_ , ^ F .
распределена так же, как величина χ2n , причем количество степеней свободы n в случае нормального распределения равно K - 3 [4]. Величина xП определяется как сумма квадратов n нормально распределенных величин z1 ожиданием, равным 0, и дисперсией, равной 1:
n
:i, ^ , Z n с математическим
X n = t zi'
i = i
Критическое значение χ2 n , отвечающее уровню значимости α , обозначается χ2 n ,α и определяется соотношением
χ n ,α
-
1 - a = J p x n ( y ) dy •
-^
Тогда область принятия гипотезы, состоящей в том, что наблюдемое распределение случайной величины совпадает с ожидаемым, определяется неравенством
22 χ n ,α
Критические уровни значимости α i для всех параметров приведены в табл. 4. Уровень значимости α0 был выбран равным 0,05. Из табл. 4 можно заключить, что α i превышает α0 только в случае A E , следовательно, гипотезу о нормальности распределения можно принять только для этого параметра.
Проверка распределений на зависимость
По полученным эмпирическим распределениям с помощью программного пакета Statistica была проведена проверка зависимости параметров медленной фазы по ранговому критерию Спирмена. Результаты этой проверки в случаях оптокинето-вестибуло-цервикального и вестибулярного нистагмов приведены в табл. 5, все коэффициенты корреляции значимы на уровне меньшем, чем 0,05. Из табл. 5 следует, что между некоторыми из пяти параметров коэффициент корреляции довольно велик, поэтому из всех параметров были выбраны три наименее зависимых (коэффициенты корреляции между ними по модулю меньше 0,3): амплитуда угла поворота глаза во время медленной фазы A E , длительность медленной фазы T S и удельная работа мышц глаза γ. Для них были посчитаны критические точки
Ткр = t кр ( a , k )
1 - р в n - 2
где t кр ( α , k ) – критическая точка двусторонней критической области распределения Стьюдента при уровне значимости α и количестве степеней свободы k = n - 2 ; ρ в – выборочный коэффициент ранговой корреляции Спирмена; n – объем выборки. Было установлено, что для ρ в в случае взаимных корреляций трех выбранных параметров выполняется неравенство ρв ≤ T кр , из чего можно сделать вывод [6], что можно принять нулевые гипотезы о незначимости взаимных корреляций между A E , T S и γ.
Критические уровни значимости и χ2 n ,α для критерия Пирсона
Таблица 2
Статистические показатели параметров медленных фаз первой группы
|
Параметр |
Оптокинето-вестибуло-цервикальный нистагм |
Вестибулярный нистагм |
||
|
µ |
σ2 |
µ |
σ2 |
|
|
ω E |
29,402 c–1 |
242,380 c–2 |
25,012 c–1 |
243,489 c–2 |
|
A H |
6,802º |
10,716 (º)2 |
8,385º |
22,505 (º)2 |
|
A Е |
7,281º |
10,577 (º)2 |
5,102º |
9,374(º)2 |
|
T S |
0,264 с |
0,015 с2 |
0,243 с |
0,022 с2 |
|
γ |
0,496 |
6,4∙10–2 |
0,479 |
7,4∙10–2 |
Таблица 3
Статистические показатели параметров медленных фаз второй группы
|
Параметр |
Оптокинето-вестибуло-цервикальный нистагм |
Вестибулярный нистагм |
||
|
µ |
σ2 |
µ |
σ2 |
|
|
ω E |
12,461 c–1 |
227,148 c–2 |
15,362 c–1 |
342,739 c–2 |
|
A H |
4,964º |
14,662 (º)2 |
6,308º |
23,932 (º)2 |
|
A Е |
4,504º |
9,249 (º)2 |
2,623º |
6,595 (º)2 |
|
T S |
0,755 с |
0,031 с2 |
0,719 с |
0,057 с2 |
|
γ |
0,812 |
0,354 |
0,968 |
0,218 |
Таблица 4
|
Параметр |
Медленные фазы первой группы |
Медленные фазы второй группы |
||||||
|
Оптокинето-вестибуло-цервикальный нистагм |
Вестибулярный нистагм |
Оптокинето-вестибуло-цервикальный нистагм |
Вестибулярный нистагм |
|||||
|
α i |
2 n ,α i |
α i |
2 n ,α i |
α i |
2 n ,α i |
α i |
2 n ,α i |
|
|
ω E |
0,3427 |
12,28 |
<10–5 |
80,13 |
0,0018 |
29,65 |
<10–5 |
54,25 |
|
A H |
0,0037 |
27,62 |
0,0042 |
27,26 |
0,0037 |
27,62 |
0,0031 |
28,12 |
|
A Е |
0,1621 |
15,47 |
<10–5 |
68,12 |
0,1762 |
15,14 |
0,0596 |
22,68 |
|
T S |
<10–5 |
87,58 |
<10–5 |
90,17 |
<10–5 |
70,19 |
0,0002 |
35,56 |
|
γ |
<10–5 |
90,13 |
<10–5 |
89,12 |
<10–5 |
51,58 |
<10–5 |
72,45 |
Таблица 5
Коэффициенты корреляции параметров медленной фазы
|
Параметр 1 |
ω E |
ω E |
ω E |
ω E |
A H |
A H |
A H |
A Е |
A Е |
T S |
|
Параметр 2 |
A H |
A Е |
T S |
γ |
A Е |
T S |
γ |
T S |
γ |
γ |
|
Коэффициент корреляции (оптокинето-вестибуло-цервикальный нистагм) |
0,22 |
0,43 |
–0,34 |
–0,54 |
0,89 |
0,49 |
0,24 |
0,19 |
0,12 |
0,27 |
|
Коэффициент корреляции (вестибулярный нистагм) |
0,19 |
0,43 |
–0,18 |
–0,46 |
0,92 |
0,42 |
0,20 |
0,16 |
0,08 |
0,24 |
Приемы моделирования параметров нистагма
Из табл. 4 следует, что в случае оптокинето-вестибуло-цервикального нистагма распределение параметра AE подчинено нормальному закону. Таким образом, для моделирования AE необходимо генерировать величины, имеющие нормальное распределение. Но в среде Delphi , в которой написана модель, есть возможность получить только равномерно распределенную на отрезке [0, 1] величину (функция random ) или случайное целое число в диапазоне от 0 до заданного числа N (функция random ( N + 1)) [2].
Для преобразования равномерно распределенной случайной величины в нормально распределенную был выбран метод, основанный на преобразовании Бокса – Мюллера [16]. Он состоит в следующем: если есть две независимые, равномерно распределенные на полуинтервале (0, 1] величины r и φ , то величины z0 и z1, определяемые формулами z0 = V-2 In r cos2пф, z1 = 4-2 ln r sin2пф, также будут независимы и распределены по нормальному закону с математическим ожиданием, равным 0, и дисперсией, равной 1. Для преобразования z0 в величину ξ распределенную нормально с математическим ожиданием, равным µ , и дисперсией, равной о2, используется линейное преобразование £ = р + оz0 [1].
Для распределений остальных параметров была отвергнута гипотеза о нормальности. Ввиду этого для их генерирования использован метод обратного преобразования, применяемый для получения случайной величины с заданной функцией распределения из равномерно распределенной величины [5]. Значения функций распределений параметров получаются из соответствующих распределений, показанных на рис. 3 и 4, по формуле n fn=Е Pi, i=1
где p i ( i = 1, 2 ... n ) - предыдущие значения плотности распределения, а fn - значения функции распределения в n- м разряде.
Моделирование медленной и быстрой фаз нистагменного цикла
Относительный угол поворота глаза φ S (τ) моделируется квадратичным законом
Ф s ( т ) = ф s ( 0 ) + а т2 + b т.
Рассмотрим случай медленной фазы первой группы. Запишем (2) в момент времени т = T S , а также учтем, что модуль интеграла от выражения ( ф s (т) - ф s (0) ) по промежутку [ 0, Ts ] равен у\ ae\ ■ Ts :
'фS (Ts ) = ФS (0) + aT + bTs
<
Ts j (a т2 + bт) dт = Y Ts\AE |.
Учитывая, что ф s ( Ts ) - ф s ( 0 ) = AE , и вычислив интеграл во втором уравнении, упростим систему:
' aT s 2 + bT s = ±| Ae\ , a3 + T = ±| Ae| Y T s .
Знак перед AE в правых частях уравнений системы выбирается противоположным знаку ω H в момент начала медленной фазы. Таким образом, решение системы записывается в виде
AA a = sign (toH (0))• у (6Y - 3), b = sign (toH (0))• (2 - 6Y). (3)
TSTS
В случае медленной фазы второй группы сначала определяется момент времени T 0 , когда скорость ω H становится равной нулю. Затем проверяется, какому из двух
T) (T ^^
интервалов принадлежит T 0: I 0, -2^ I или I -2^ , Ts I . Если к первому, то знак AE выбирается совпадающим со знаком ω H в момент начала медленной фазы. Иначе знак AE выбирается противоположным знаку ω H в момент начала медленной фазы. Момент T 0 задает ось параболы (2), а в вершине производная (2) равна нулю, поэтому можно записать систему
' 2 aT 0 + b = 0,
<
aT s + bTs =- sign ( to H (0) ) • sign
Решив эту систему, получаем выражения для коэффициентов a и b :
a = sign ( to H (0) )•! ae|
2TST. - T
, b = -
si gn ( to H (0) ) •! a e\T0
т T T - T S 0
Поэтому значения коэффициентов a и b , вычисленные по этим формулам, заканчивают определение закона (2).
Быстрая фаза моделируется как вращение глаза в сторону, противоположную направлению предыдущей медленной фазы, описываемое законом вида
Ф F ( т ) = ф S ( TS ) + d cos k ( т - TS ) .
Чтобы найти коэффициенты d и k , примем два предположения: первое – из работы [14], второе – из [21]:
-
1) максимальная относительная угловая скорость глаза достигается в середине саккады;
-
2) концы быстрых фаз лежат на графике угловой скорости головы (известной из входного файла), умноженной на размерный коэффициент усиления; в случаях оптокинето-вестибуло-цервикального и вестибуло-цервикального нистагмов этот коэффициент равен 0,4 c, а в случае оптокинето-вестибулярного и вестибулярного нистагмов – 0,1 c.
Исходя из этих двух предположений и известного времени T F можно найти значение угла поворота глаза в конце быстрой фазы ф F ( TS + T F ) . Введем величину
AF = фF (TS + TF ) — фF (TS ) , равную амплитуде текущей быстрой фазы. Тогда закон фF (т), имеющий вид
A Г п (т - TS)
фF ( т ) = ФS ( TS )- 4F cos ---- - 1 ,
-
2 V TF 7
удовлетворяет обоим предположениям модели.
Алгоритм моделирования
-
1. В начале очередной медленной фазы по известному закону распределения генерируется значение параметра TS и определяется группа медленной фазы.
-
2. Если медленная фаза принадлежит первой группе, то по известным законам распределения генерируются значения параметров γ и AE , если второй – генерируется значение параметра AE и определяется момент времени T 0 , когда абсолютная угловая скорость головы ω H обращается в нуль.
-
3. В зависимости от группы медленной фазы по формулам (3) или (4) вычисляются коэффициенты a и b , и медленная фаза моделируется законом (2).
-
4. По известному закону распределения генерируется значение параметра TF .
-
5. По формуле (5) рассчитывается значение амплитуды быстрой фазы AF , и быстрая фаза моделируется законом (6).
Моделирование одного цикла медленная фаза – быстрая фаза завершено, и этот процесс можно применить ко всем данным во входном файле. Примеры модельных реализаций оптокинето-вестибуло-цервикального и вестибулярного нистагмов приведены на рис. 5.
Оценка модели
Для сравнения распределений параметров экспериментальных записей с распределениями параметров модельной траектории выполнены следующие действия:
-
1) по начальным данным каждой из 20 записей каждого вида построены модельные реализации;
-
2) собрана статистика параметров модельных реализаций;
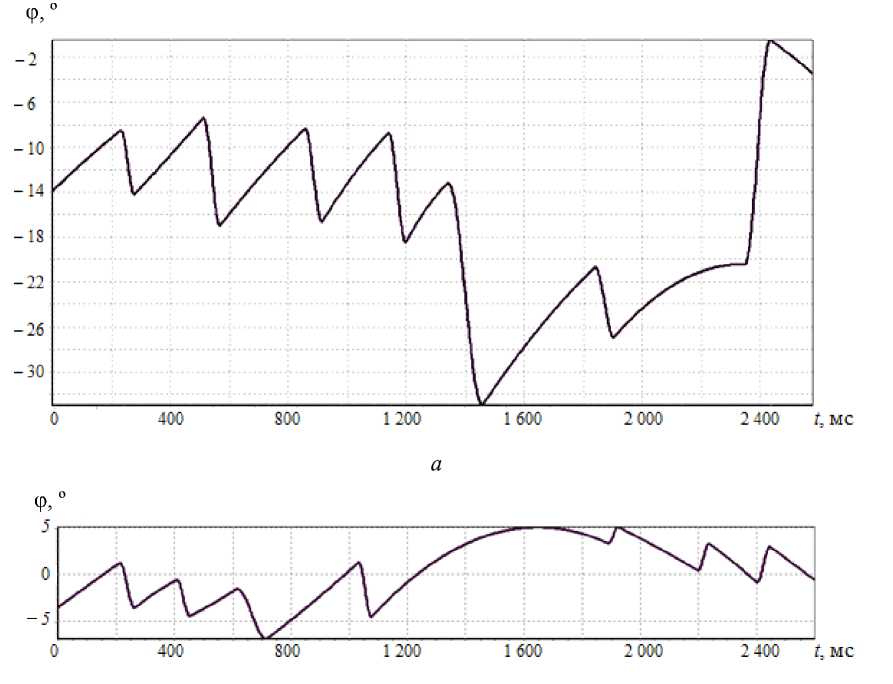
б
Рис. 5. Модельные реализации: а – оптокинето-вестибуло-цервикальный нистагм; б – вестибулярный нистагм
-
3) для сравнения распределений параметров модельных и экспериментальных траекторий был применен критерий Пирсона; уровень значимости, как и выше, принят равным 0,05.
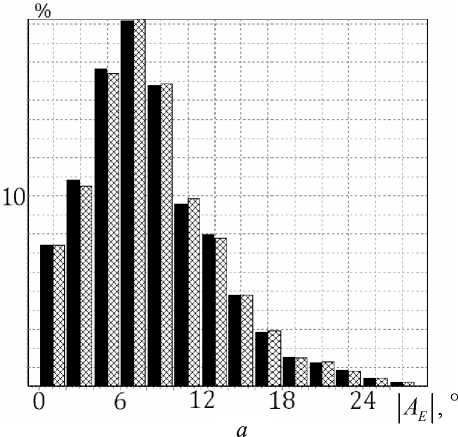
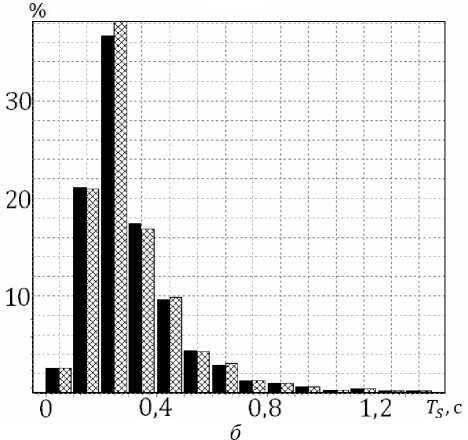
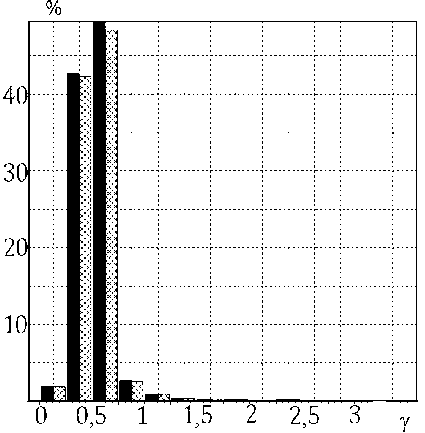
Гистограммы распределения параметров модельных реализаций в случаях оптокинето-вестибуло-цервикального и вестибулярного нистагмов показаны на рис. 6.
Критические значения уровня значимости для критерия Пирсона для распределений трех параметров в случае оптокинето-вестибуло-цервикального и вестибулярного нистагмов приведены в табл. 6. Для всех параметров критический уровень превосходит выбранный уровень значимости 0,05, следовательно, модель приближена к реальному процессу нистагма с достаточной степенью достоверности.
Таблица 6
Критические значения уровня значимости критерия Пирсона
|
Параметр |
Оптокинето-вестибуло-цервикальный нистагм |
Вестибулярный нистагм |
|
γ |
0,8214 |
0,7982 |
|
1 A E |
0,6205 |
0,7251 |
|
т S |
0,7821 |
0,7386 |
12 18
г
A E ,
д
,,
,
γ
е
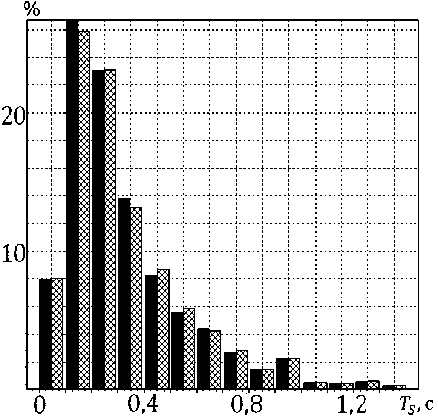
Рис. 6. Экспериментальные (слева) и модельные (справа) распределения в случаях оптокинето-вестибуло-цервикального: а – AE ; б – TS ; в – γ; и вестибулярного нистагмов: г – AE ; д – TS ;
е – γ
Заключение
Во многих случаях человек-оператор, являясь одним из звеньев в системе управления динамическим объектом, может находиться в условиях движения. Возникающие в этой ситуации вестибуло-окулярные реакции, несомненно, эволюционно оправданные и целесообразные, могут быть как полезны, так и, наоборот, вредны. В обоих случаях может стоять вопрос о роли вестибуло-окулярных реакций в восприятии оператором окружающей визуальной обстановки, о его способности сохранять работоспособность в условиях движения.
Описанная ситуация дает возможный пример применения статистической модели нистагма. Получив лабораторную запись нистагма оператора в предполагаемой динамической обстановке, разработчик в дальнейшем имеет возможность, пользуясь статистической моделью, многократно получать реализации нистагма для расчетов и оценок при работе над динамическим объектом, не привлекая более для этого оператора.
На основе обработки данных экспериментальных записей нистагменных циклов создана статистическая модель нистагма. Были сгенерированы две серии модельных реализаций, которые при помощи критерия Пирсона были сравнены с двумя сериями экспериментальных записей. Во всех случаях критическое значение уровня значимости критерия Пирсона превосходит установленный уровень значимости, что позволяет сделать вывод, что данная модель достаточно точно приближает реальный процесс оптокинето-вестибуло-цервикального и вестибулярного нистагмов.
Благодарности
Работа выполнена при поддержке гранта РФФИ № 12-01-00839.
Список литературы Математическое моделирование вестибулярного нистагма. Часть I. Статистическая модель
- Андронов А.М., Копытов Е.А., Гринглаз Л.Я. Теория вероятностей и математическая статистика. -СПб.: Питер, 2004. -461 с.
- Архангельский А.Я. Программирование в Delphi 7. -М.: Бином, 2004. -1152 с.
- Бабияк В.И. Реакции глазодвигательного аппарата и их сенсорные компоненты при сочетанном действии вестибулярных и зрительных раздражителей: автореф. дис.. д-ра. мед. наук. -Л., 1977. -23 с.
- Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. -М.: Мир, 1971. -408 с.
- Вадзинский Р.Н. Справочник по вероятностным распределениям. -СПб.: Наука, 2001. -295 с.
- Гмурман В.Е. Теория вероятностей и математическая статистика. -М.: Высшая школа, 2003. -479 с.
- Доценко В.И., Егорова Е.А., Каспранская Г.Р., Муратова Е.А., Сучалкина А.Ф., Якушев А.Г. Экспериментальное и математическое моделирование вестибулярного нистагма у здоровых людей и больных ДЦП//Фундаментальная и прикладная математика. -2005. -Т. 11, № 8. -С. 195-204.
- Левашов М.М. Нистагмометрия в оценке состояния вестибулярной функции//Проблемы космической биологии. -Л.: Наука, 1984. -Т. 50. -222 c.
- Митькин А.А. Системная организация процессов зрения: дис. … д-ра. психол. наук/Ин-т психологии АН СССР. -М., 1984. -494 с.
- Орлов И.В. Вестибулярная функция. -СПб.: Наука, 1998. -248 с.
- Корюкин В.Е. Роль и значение центральных нервных механизмов в генезе вестибулярных реакций (клинико-экспериментальное исследование): автореф. дис. … д-ра. мед. наук. -Л., 1986. -42 с.
- Филин В.А. Автоматия саккад. -М.: Изд-во МГУ, 2002. -240 с.
- Штефанова О.Ю. Математическое моделирование и оценка качества системы зрительной ориентации в горизонтальной плоскости: дис. … канд. физ.-мат. наук. -М.: Изд-во МГУ, 2011. -179 с.
- Якушев А.Г., Напалков Д.А., Ратманова П.О., Кручинина А.П., Штефанова О.Ю., Гинзбург Е.А. Композиционный способ определения управления глазодвигательными мышцами при саккаде//Российский журнал биомеханики. -2011. -Т. 15, № 1. -С. 99-109.
- Якушев А.Г., Штефанова О.Ю., Сучалкина А.Ф., Каспранская Г.Р. Математическое моделирование нистагма как механизма стабилизации взора при движении//Изв. Ин-та инженерной физики. -2009. -№ 14. -С. 25-29.
- Box G.E.P., Muller M.E. A note on the generation of random normal deviates//The Annals of Mathematical Statistics. -1958. -Vol. 29, № 2. -P. 610-611.
- Darlot C., Merfeld D.M., Zupan L.H. Using sensory weighting to model the influence of canal, otolith and visual cues on spatial orientation and eye movements//Biological Cybernetics. -2002. -№ 86. -P. 209-230.
- Fernandez C., Goldberg J. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. II. Response to sinusoidal stimulation and dynamics of peripheral vestibular system//J. Neurophysiol. -1971. -Vol. 34. -P. 661-675.
- Ramat S., Schmid R., Zambarbieri D. Eye-head coordination in darkness: Formulation and testing of mathematical model//Journal of Vestibular Research. -2003. -№ 12. -P. 79-91.
- Schmid R. Systems analysis of the vestibulo-ocular system//Fifth symposium on the role of the vestibular organs in space exploration/Naval Aerospace Medical Institute, Naval Aerospace Medical Centre, 19-21 August 1970. -Pensacola, 1970. -P. 237-249.
- Schmid R., Zambarbieri D. Strategies of eye-head coordination//Oculomotor control and cognitive processes. -New York: Elsevier Science, 1991. -P. 229-246.


