Математическое моделирование вестибулярного нистагма. Часть II. Механико-информационная модель

Вестибулярный нистагм является одним из древнейших эволюционно закрепившихся рефлексов, играющих важную роль в жизни человека.

Моделирование этой вестибуло-глазодвигательной реакции, как и других, является насущной задачей. Можно указать несколько прикладных областей, в которых имеется актуальная потребность в таких моделях. Прежде всего следует упомянуть медицинские приложения, например [2, 4, 18], в которых использование математических моделей позволяет оценивать тяжесть состояния больного и следить за динамикой заболевания. Показано также, что мониторинг вестибуло-окулярных реакций может быть полезен для оценки функционального состояния человека-оператора, подверженного

Сучалкина Анна Федоровна, старший эксперт ОАО «ВымпелКом», Москва высокому уровню напряженности труда и профессионального стресса [3]. Моделирование вестибуло-окулярных реакций, несомненно, необходимо при решении весьма актуальной и интересной задачи создания вестибулярного протеза [8]. Наконец, модели движения глаз человека могут быть полезны при создании или проектировании биомехатронных систем, опирающихся на зрение человека [11], или при разработке антропоморфных роботов, обладающих системой технического зрения [14].

Обзор литературных источников, посвященных вопросам моделирования вестибулярного нистагма, приведен в работе [1]. Там же приводится описание использованного экспериментального оборудования и сценариев проведения лабораторных исследований.

При математическом описании модели будут использованы системы координат и обозначения промежутков времени и переменных, введенные в работе [1].

Структура модели

В работе рассматривается моделирование движения глаз испытуемого, сидящего прямо на вестибулярном кресле в условиях темноты, для случая пассивного вращения вокруг вертикальной оси. На рис. 1 приведена общая схема механико-информационной модели вестибулярного нистагма. Модель получила такое название, потому что в ней воспроизводятся как механические, так и информационные процессы, протекающие при реализации нистагма.

В структуре модели можно условно выделить четыре основных блока:

• 1.    Оценка движения головы и формирование медленной фазы нистагма. Входным звеном вестибуло-окулярных реакций является механическое движение купул полукружных каналов и мембран отолитов, вызываемое воздействием сил инерции, возникающих при ускоренном движении головы. Связанный с этим движением изгиб волосковых пучков волосковых клеток изменяет ионные токи, протекающие в вестибулярном рецепторе. В модели в качестве носителя полезного сигнала рассматривается изменение частоты афферентной импульсации в первичном вестибулярном нейроне. После этого моделируются оценки углового ускорения головы, которые строятся вестибулярными ядрами по информации, поступающей от полукружных каналов и отолитов. На основе этих оценок, взятых с соответствующими весовыми коэффициентами, вычисляется относительное угловое движение глаз, которое после наложения на него быстрых фаз будет составлять медленную фазу нистагма.

• 2.    Логика переключения фаз. Переключение от медленной фазы к быстрой происходит в те моменты времени, когда некоторая бинарная случайная величина, подчиняющаяся марковскому закону, принимает значение, равное единице, а также одновременно выполнены следующие четыре условия:

• 1)    абсолютная величина относительного угла поворота глаза превысила заданное пороговое значение;

• 2)    амплитуда угла поворота глаза за текущую медленную фазу превысила пороговое значение;

• 3)    величина угловой скорости глаза превысила пороговое значение;

• 4)    от момента окончания предыдущей быстрой фазы прошло достаточное время, которое исключает наложение быстрых фаз.

• 3.    Моделирование быстрой фазы. Для задания быстрой фазы нистагма определяются ее амплитуда и длительность как случайные величины с известным законом распределения, зависящим от текущего значения абсолютной угловой скорости головы. Траектория движения глаза во время быстрой фазы представляет собой косинусоиду, заданную на половине периода.

• 4.    Задание движения глаз. При движении глаза в горизонтальной плоскости поворот осуществляется за счет согласованного сокращения и расслабления внутренней и наружной прямых мышц глаза. В данном блоке формируются команды для этих мышц.

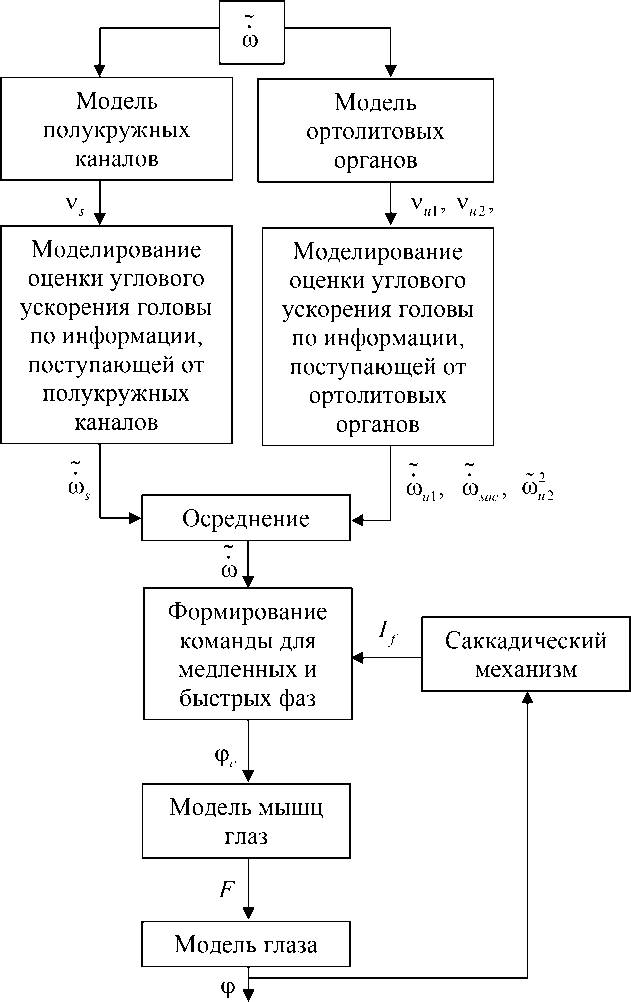
Рис. 1. Общая схема модели нистагма

Формирование медленной фазы нистагма

Для моделирования движения купулы полукружного канала в условиях ускоренного углового движения головы используется первая часть модели Голдберга– Фернандеса [13], записанная в виде передаточной функции:

X s , i ( S ) = (- 1) ' H 1 ⁽ S ) S to⁽ S ) = (- 1) '

^Т 1 ^Т 2

(1 +Т₁ S )(1 +Т₂ S )

s to( s ), i = 1;2,

где x_s , _i описывает угловое смещение купулы; s to - угловое ускорение головы; Т 1 и Т 2 -большая и малая постоянные времени полукружного канала; i = 1; 2 обозначают левый и правый полукружные каналы соответственно.

На выходе получается величина v _s , _i , которая пропорциональна изменению афферентной импульсации, возникающей в вестибулярных механорецепторах:

v s , i ⁽ S ⁾ = H 2 ⁽ S ⁾ X_s , i ⁽ S ⁾ = к о

^Т _aS (1+Т _aS )

⁽ 1+т / s ⁾ x_s , i ⁽ s ⁾, i = 1;2,

. . . . спайк/с где к о - константа, имеющая размерность _гр_ад .

Поскольку вестибулярные рецепторы являются эволюционно одними из самых древних, предполагается, что в центральной нервной системе сформировалась внутренняя модель вестибулярного аппарата [17], которая позволяет получить внутреннюю оценку углового ускорения головы. Таким образом, величина sto5, i ( S ) = (- 1) 'H,(S )• H2(s )•—V,Д s ) =

= (-<)

' ( 1 + Т | S )( 1 + Т 2 S )

^Т 1 ^Т 2

• ¹     (Hj o Z l

( 1+Т _/S )     T _as    к_о^s , ' ^{( S} ^      ^1;2

моделирует внутренние оценки абсолютного углового ускорения головы, построенные в центральной нервной системе по информации, поступающей от полукружных каналов.

Линейное ускорение, возникающее во время вращения вокруг вертикальной оси, можно разложить на две составляющие: тангенциальную и центростремительную. Соответственно, на мембраны отолитов действуют силы инерции. Сила, направленная тангенциально, воздействует на утрикулярную и саккулярную мембраны, а направленная центробежно - только на утрикулярную. Вследствие воздействия сил инерции происходит смещение мембран отолитового аппарата.

Согласно модели, предложенной в работе [17], для случая вращения вокруг вертикальной оси можно написать следующие уравнения, позволяющие для утрикулюсов получить величины v _U 1, ' ( s ) и v _U 2, ' ( s ) и для саккулюсов - величины v _sac , _{ ( s ), которые пропорциональны изменению частоты афферентной импульсации (спайк/с), порождаемой механорецепторами отолитовых органов:

.                           .          (1 + Т _Ss )

v U 1 , i ⁽ s ⁾ = ⁽- 1^{) l}H₀ ⁽ S ⁾ S to⁽ s ⁾р = ⁽- 1⁾ ' К——-------------s to⁽ S ⁾р,

^,                                        (1 + Т о 1 S )(1+т о 2 S )

• • о                •          (1 + Т _Ss )          ,

v U 2, i ⁽ S ⁾ = ⁽- 1⁾ ' H o ⁽ s ⁾to ^{2 (} S ⁾р = ⁽- 1⁾ ' К-— ------------- to ^{2 (} S ⁾р,

^,                                    (1+Т о 1 s )(1+Т о 2 s )

.                           .          (1 + Т _Ss )

vsac,i(S) = (- 1)'Ho(s)Sto(S)р = (- 1)'К (1 +Т ^s)(1 +Т 2S) Sto(S)р, где К, т01, Т02, Тs - известные константы; i = 1; 2 - для левого и правого утрикулюсов и саккулюсов; р - расстояние от центра масс утрикулюса и саккулюса до оси вращения.

В центральной нервной системе образуются внутренние оценки абсолютного углового ускорения головы, построенные по тангенциальным составляющим ускорения:

1      ~              1       1 (1+т₀ i S )(1+т_{о 2} S )

.5и 1,i(s) = -(- 1)Н°(s)vи 1,(s) = -(- 1)-----°1         °2 } vи 1,(s), р                        Р ^      (1 + LSS)

1      ~              1       1 (1+т ° 1 S )(1+т ° 2 S )

S ⁵ s _ac , i ⁽ S ⁾ = р ^{(-1) Н}° ⁽ S ^)v sac , i ⁽ S ⁾ = р ^{(- 1)}^------ ^ _{1 + т S} ) ------^Vsac , i ⁽ S ^

Рассмотрим утрикулярный сигнал о центростремительном ускорении, для которого можно записать приближенное равенство:

^v и 2, i =№²) ^-.f(®^{2 )} ~ ²® о /(® о )^А®.

Таким образом, по информации, поступающей от утрикулюса, можно построить оценку абсолютной угловой скорости головы tou 2,i( s ) =

(      . Ho ( s )v u 2j( s ) =     (-1)i . (1 + T o1 s)(1 + T o 2 s)

V u 2i ( s )

2 ^ 0 f ( to 0 ) p                  2 K to o f ( to 0 ) p      (1 it s s )

Для получения осредненной оценки абсолютного углового ускорения головы выписывается следующее соотношение:

_        1 1 ( stou 1,1 (s) + stou 1,2 (s sto(s) = 2--—--------

)    s to u 2,1 ( s ) + s to u 2,1 ( s )    s to sac ,1 ( s ) + s to sac ,2 ( s )

s to s Д s ) + s to s ,2 ( s )

+

.

Далее в модель включается уравнение, связывающее оценку абсолютного углового ускорения головы и командное относительное угловое ускорение глаза. Благодаря вестибуло-окулярному рефлексу происходит компенсаторный поворот глазных яблок с ускорением, противоположным по направлению абсолютному ускорению головы. Как известно [6], отношение среднего относительного углового ускорения глаза на протяжении медленной фазы к среднему абсолютному угловому ускорению головы на том же промежутке называют коэффициентом усиления kS. Коэффициент усиления не является постоянным и изменяется от цикла к циклу, поэтому при моделировании медленной фазы он считается случайной величиной с известным законом распределения. Таким образом, в модели определяется s 2ф S ( s ) = -kS (п ) s to( s ), где s2фS - командное относительное угловое ускорение глаза; п - номер текущей медленной фазы. Поскольку в начальный момент времени требуется выполнение условий sфS(0) = 5(0) = 0 и фS(0) = 0(0) = 0, получается

Ф s ( s ) =-ks (п )0( s ), где фS - командный угол поворота глаза на протяжении медленной фазы; 0 - оценка абсолютного углового положения головы.

Переключение между медленной и быстрой фазами

Саккадический механизм, использующий обратную связь от мышц глаз [16], обеспечивает переключение фаз нистагма. Для моделирования работы саккадического механизма рассматривается бинарная случайная величина z , принимающая значения 0

или 1 по заданному вероятностному закону (рис. 2). Матрица вероятностей переходов от одного значения к другому имеет вид р 1- р

P 11- q    q J ¹

где р и q - вероятности того, что переменная остается в состоянии 1 и О соответственно. В дискретные моменты времени с шагом At = О,ОО1 с разыгрываются значения переменной z .

Считается, что пока величина z имеет значение О, переключение от медленной фазы к быстрой невозможно, а как только случайная величина принимает значение 1, проверяются условия возможности переключения к быстрой фазе.

Текущая медленная фаза нистагма с номером и в момент времени t_z прерывается быстрой фазой, только если одновременно выполняются следующие пять условий:

• 1)    случайная величина z , заданная марковским законом с приведенной выше матрицей вероятностей переходов, в момент времени t_z приняла значение, равное 1;

• 2)    командный угол поворота глаза ф _s ( t_z ) превысил пороговое значение ф _т :

|ф s ( t z )| > Ф т ;

• 3)    амплитуда поворота глаза за текущую медленную фазу превысила пороговое значение ф _а :

|ф s ⁽ t z ⁾ - ф( t s )| > ф _а ;

• 4)    относительная угловая скорость глаза превысила пороговое значение ® _т : ^{| ф} s ⁽ ? z )| > ® т ;

• 5)    чтобы не произошло наложения быстрых фаз, проверяется условие

^tz^{- t} s > ^td ¹

где t d - некоторая заданная константа.

Неравенства 2), 3) и 4) задают минимальные угол поворота глаза, амплитуду поворота глаза и скорость поворота глаза, при которых медленная фаза нистагма прерывается быстрой фазой. Условие 4) не позволяет прерывать быстрыми фазами медленные фазы непосредственно после того, как произошла смена знака угловой скорости головы.

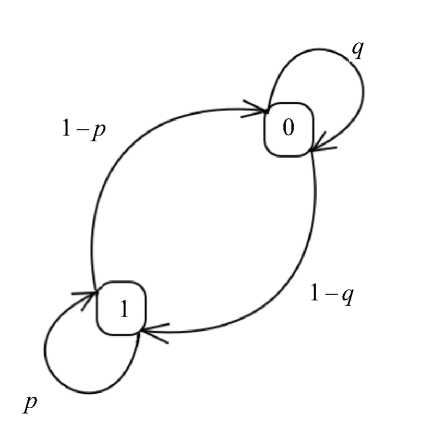
Рис. 2. Состояния и вероятности переходов

Таким образом, когда угол поворота глаза превышает значение ф _т , амплитуда медленной фазы нистагма превышает значение ф _а , скорость поворота глаза превышает значение ю _т и не происходит наложения быстрых фаз, как только цепь Маркова генерирует значение z =1, медленная фаза нистагма прерывается быстрой фазой.

Моделирование быстрой фазы

Моделирование быстрого саккадического движения для каждой конкретной саккады осуществляется определением значений двух параметров: амплитуды А и длительности Т саккады, как это было предложено в работе [10].

Для задания быстрой фазы нистагма используется часть косинусоиды, причем при определении направления саккадического скачка учитывается, является на момент переключения функция ф ₅ ( t ) , описывающая медленную фазу нистагма, возрастающей или убывающей:

5( t ) = sign^ 5 ( t j )) А _f cos

л( t - t f )

Т/

^{t G[ t}f Jf+T ¹ .

Здесь A f и T j - амплитуда и длительность текущей быстрой фазы, случайные величины, формирующиеся следующим образом. Длительность T J генерируется как случайная величина, имеющая усеченное нормальное распределение на отрезке [ Т ₁ ; Т ₂ ] (табл. 1). После этого генерируется случайная величина A f , имеющая усеченное нормальное распределение на отрезке [ A i ; A 2 ] причем дополнительно проверяется

А условие, что отношение т попадает в интервал [v 1; v2] (см. табл. 1).

Таким образом, полностью сформирован закон движения глаза на протяжении текущего цикла нистагма ф5(t) - Ф5(ts) + фс(ts), t G [ts; ts + Ts], ф с (t) = |

tf t Ы( t f ) + ф с (t f ), t G[ t _/; t _/+ T f |,     ^{L !} - ' ^т- -

Здесь ф _с - команда, подающаяся на глазодвигательные мышцы.

Управление мышцами глаз

На основании результатов исследований можно сделать вывод, что у здорового человека значения параметров нистагма для правого и левого глаз практически совпадают, поэтому далее строится модель движения одного глаза. Для примера рассматривается правый глаз.

Задаются управления для внутренней и наружной прямых мышц глаза, при этом используется композиционный способ построения управления [12]:

V/(t) =v Tj (t) +vSj (t) +vк/ (t) + vDj (t), где v/ - управление,/-й мышцы, имеющее следующие составляющие: vт/ - тоническую, vsj - статическую, vк/ - кинематическую, vd/ - динамическую; управления имеют размерность силы, у = 1; 2.

Составляющие задаются следующим образом. Тонические компоненты постоянны и представляют собой долю ц максимальной силы vmax, развиваемой мышцей:

• ^V    Т 1 ^{( t )} = ^V Т2 ^{( t )} = P^V max -

• Статические компоненты определяются упругими свойствами мышц:

• V    S 1 ⁽ t ⁾ = kR ф _c ⁽ t ⁾, v S2 ⁽ t ⁾ = - kR ф _c ⁽ t ⁾, где к - коэффициент упругости мышцы; R - радиус глаза. Кинематические компоненты характеризуют вязкие свойства мышц:

V К 1 ⁽ t ⁾ = gR ф _c ⁽ t ⁾, V _К 2 ⁽ t ⁾ = -gR ф _c ⁽ t ⁾, где g - коэффициент вязкого трения. Наконец, динамические компоненты управления определяются инерционными характеристиками глаза:

^V D 1 ^{( t )} = ^

j MR ф _c(t), ф _c ( t ) >  0, 0, ф _c ⁽ t ⁾ < 0,

V D 2 ⁽ t ) = ^

j MR ф _c(t), ф _c(t) <  0, 0,    ф _c (t )>0,

где M - масса глаза.

Обозначив силы, развиваемые мышцами глаза, через F 1 и F 2 , запишем уравнения

Fj(t) = k(lj(t)-lо) + glj(t) + vy(t), j = 1; 2, где lj(t) - текущая длина мышцы; l0 - длина мышцы в ненапряженном состоянии, поэтому 11 (t) =/0-Rфc(t) и 12(t) =/0 +Rфc(t). Величина силы, развиваемой мышцей, считается положительной, если она является тянущей.

Завершает модель уравнение движения глаза

Iф( t)=R (F1 (t)-F2< t)), где I - момент инерции глаза относительно оси вращения Oz, I = 5MR .

Результаты моделирования. Сравнение с результатами исследований

В табл. 1 приведены значения констант модели и указаны законы распределения параметров, являющихся случайными величинами.

Среди перечисленных выше параметров обсудим дополнительно коэффициент усиления k_s , который не обсуждался в работе [1]. Его значения были вычислены как отношения амплитуды поворота глаза к амплитуде поворота головы для всех медленных фаз нистагма. Распределение значений k_s показано на гистограмме (рис. 3). С помощью теста Лиллиефорса в приложении MATLAB проверено, что значения k_s этой записи имеют усеченное нормальное распределение [15]. Уровень значимости Р выбран равным 0,05. Для выбранного массива числовых значений коэффициента усиления k_s в приложении MATLAB были вычислены его математическое ожидание и среднеквадратическое отклонение, они внесены в табл. 1.

На основании выписанных выше уравнений и данных табл. 1 в среде Simulink приложения MATLAB написана программа, реализующая механико-информационную модель нистагма. На вход программы подается числовой массив, моделирующий экспериментальный стимул - угловое положение головы 0( t ). Движение головы после начального поворота представляет собой синусоидальное вращение с периодом 8 с и амплитудой 60°. Детали эксперимента описаны в работе [1]. В результате выполнения программы получается модельная траектория, отвечающая вестибулярному нистагму, который возникает у здорового человека в ответ на входной стимул (рис. 4).

Таблица 1

Параметр	Значение	Размерность	Источник
Т1	5,7	c	Из литературы
т2	0,003	c	Из литературы
к 0	29,24	спайк/(град-с)	Подбирается по результатам испытаний для обеспечения качественного совпадения
Т а	80	c	Из литературы
т /	0,049	c	Из литературы
К	33,3	—	Из литературы
т .	10	c	Из литературы
т о 1	5	c	Из литературы
т о 2	0,016	c	Из литературы
Р	0	—	Не изменяется
q	0,98	—	Подбирается
а .	И = 0,08, о = 0,11	град	Подбирается
b	7	—	Подбирается
Т	И = 37, о = 40	мс	Подбирается
т 1	35	мс	Подбирается
Т 2	160	мс	Подбирается
а 1	1,54	град	Подбирается
а 2	33	град	Подбирается
V 1	0,03	град/c	Подбирается
V 2	0,1015	град/c	Подбирается
t d	120	мс	Подбирается
V а	1	град	Из собственных исследований
V m	1,1	град	Из собственных исследований
to s	1	град/c	Из собственных исследований
ks	И = 0,48, о = 0,2	—	Из собственных исследований
И	0,05	—	Из литературы
^ max	0,0245	н	Из литературы
К	0,0856	Н/м	Из литературы
R	0,0127	м	Из литературы
G	0,0342	Н-с/м	Из литературы
^ 0	0,03	м	Из литературы
M	0,0107	кг	Из литературы

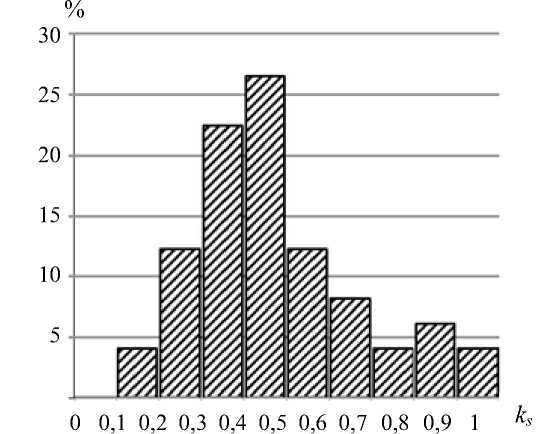
Рис. 3. Гистограмма коэффициента усиления

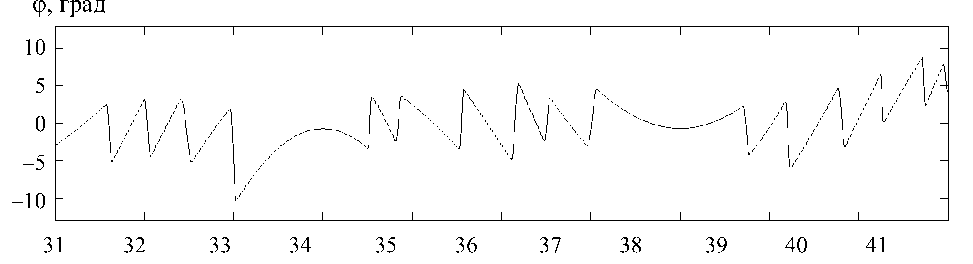
t , c

Рис. 4. Фрагмент модельной траектории

Было проведено сравнение распределений параметров нистагма, полученных в результате моделирования, с распределением параметров нистагма, записанного при исследовании одного из испытуемых, а также с распределением параметров траектории, полученной с помощью статистической модели [1]. Сравнивались распределения четырех параметров: длительностей Ту и T_s и амплитуд А у и A_s быстрых и медленных фаз нистагма. Для сравнения были построены гистограммы этих параметров (рис. 5). Величина экспериментальной выборки (количество циклов нистагма) и ₁=53, величины выборок, полученных для механико-информационной и статистической моделей, одинаковы и равны и ₂ = и ₃ = 63. По формуле к = 5 lg( n ), где n = min( n 1 , n 2 , n ₃), вычислено количество интервалов для гистограмм к =9 [9].

Для попарного сравнения распределений использовался индекс I чс Чекановского-Съеренсена [7]. Поскольку для сравнения выборок параметров играет роль только количество частот, попавших в каждый из интервалов, гистограммы для всех четырех параметров были объединены в одну гистограмму. Таким образом, объединенная гистограмма имеет 36 столбцов. По формуле 2 к-2 число степеней свободы получается равным 70 [5]. Статистический уровень значимости Р выбран равным 0,05. В табл. 2 приведены значения индекса I чс , а также величина t , которая показывает статистическую значимость отличия дополнения (1- I чс ) от нуля, и критическое значение, взятое из таблицы Стьюдента.

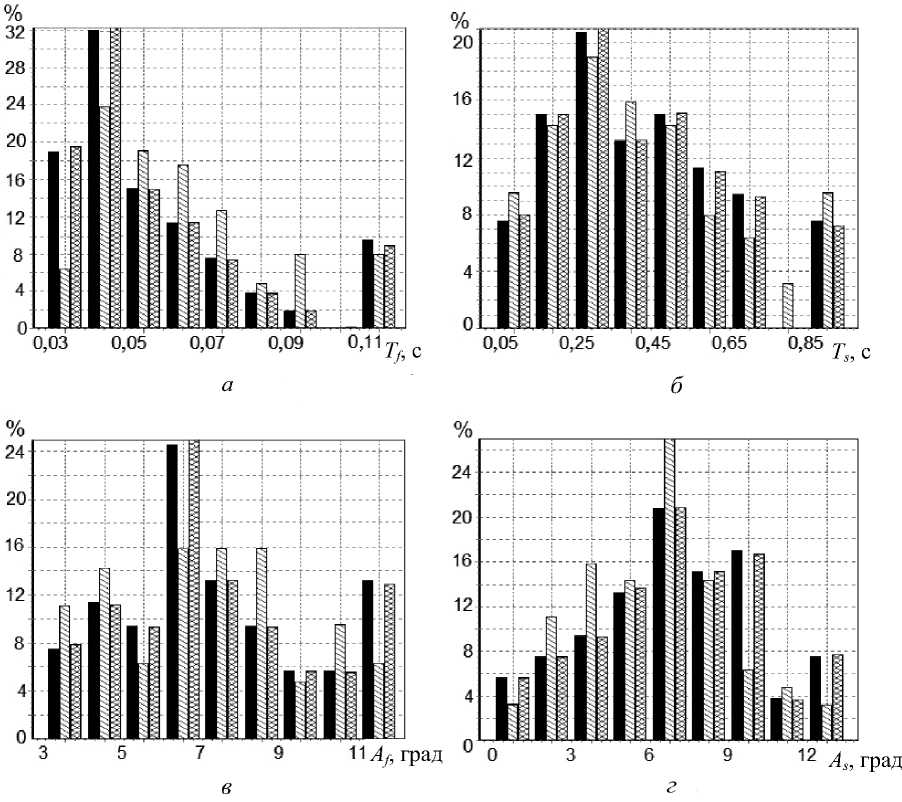
Рис. 5. Гистограммы параметров нистагма (эксперимент (слева), механикоинформационная (в середине) и статистическая (справа) модели): а - длительности быстрых фаз; б - длительности медленных фаз; в - амплитуды быстрых фаз; г -амплитуды медленных фаз

Таблица 2

Сравнение распределений параметров экспериментального и модельных нистагмов с помощью индекса Чекановского-Съеренсена

Сравнение	I ЧС	t	tCm
Эксперимент - механико-информационная модель	0,825	1,483	1,994
Эксперимент - статистическая модель	0,884	0,956
Механико-информационная модель - статистическая модель	0,833	1,475

В результате всех трех сравнений оказалось, что параметр t имеет значения, существенно меньшие критического значения t c _m . Этот факт позволяет сделать вывод о том, что в этих трех случаях нулевая гипотеза о принадлежности выборок одной генеральной совокупности статистически подтверждается, т.е. распределения параметров модельных нистагмов, полученных с помощью механико-информационной и статистической моделей, достаточно хорошо соответствуют как друг другу, так и распределению параметров нистагма, записанного в лабораторных условиях.

Заключение

На базе вестибулометрического комплекса проведено изучение вестибулярного нистагма, возникающего при вращении с ускорением. На основе обработки экспериментальных записей нистагменных циклов создана механико-информационная модель вестибулярного нистагма. Для этой модели подобран такой набор параметров, что модельная траектория глаз имеет те же характеристики, что и запись нистагма здорового испытуемого. Распределения параметров нистагма, записанного в эксперименте, сравнены с помощью индекса Чекановского-Съеренсена с аналогичными распределениями параметров модельных траекторий, полученных с помощью механико-информационной и статистической моделей. При выбранном уровне значимости можно говорить об отсутствии достоверного различия между выборками. Таким образом, можно заключить, что была успешно построена механикоинформационная модель вестибулярного нистагма и подобраны значения ее параметров для одного из испытуемых. Предложенная модель является достаточно компактной, при этом в ней нашли отражения основные механические и информационные процессы, протекающие во время реализации вестибулярного нистагма.