Математическое моделирование влияния внешних воздействий на температурные показатели масел двигателя внутреннего сгорания и элементов трансмиссии

Проведенный анализ работ [2, 4, 5] показывает, что для описания процессов, происходящих в ДВС и элементах трансмиссии, используются различные математические модели. В данной работе применяется раздел математической статистики – планирование эксперимента. Для оценки влияния внешних воздействий на температурные показатели масел ДВС и элементов трансмиссии был реализован полный факторный эксперимент, который направлен на определение температуры масла ДВС, коробки передач и главных передач. Моделирование влияния внешних воздействий на температурные показатели масел ДВС и элементов трансмиссии заключалось в следующем: строилась концептуальная модель; проводилась её формализация и исследование моделируемого процесса; определялись необходимые аппроксимации; строилась обобщённая схема процесса; по этой обобщённой схеме создавался алгоритм и разрабатывался программный комплекс; проводились расчёты на ЭВМ; определялись математические и графические зависимости внешних воздействий на температурные показатели масел ДВС и элементов трансмиссии; разрабатывались практические рекомендации по процессу подогрева применительно к эксплуатационным условиям СНО ОП.

Подогрев масел двигателя и элементов трансмиссии осуществляется системой подогрева, принципиальная схема которой представлена на рисунке 1.

Объектом исследования на данном этапе исследований (полного факторного эксперимента) является температура окружающего воздуха, время работы системы подогрева и мощность теплового агрегата, влияющие на температуру масел ДВС, коробки передач, главных передач ВАТ.

Задача сводится к определению такой мощности теплового агрегата, при которой достигается максимальное значение температуры масла за минимальное время. Факторы, влияющие температуру масла ДВС, КП, ГП, представлены на рисунке 2.

Выбираются основные входные (управляемые) факторы, определяющие условия работы системы подогрева: Т ов – температура окружающей среды, °С; t – время работы системы подогрева, мин; W ТА – мощность теплового агрегата, кВт.

За основные оценочные показатели (выходные факторы) принимаются показатели температуры масла: температура масла ДВС Т ДВС , °С; температура масла КП Т КП , °С; температура масла ГП Т ГП , °С.

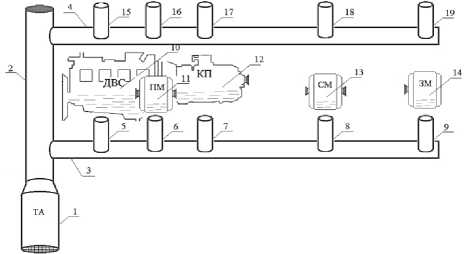
Рисунок 1. Принципиальная схема системы подогрева масел двигателя и элементов трансмиссии: 1 – тепловой агрегат; 2 – основная магистраль подвода теплоты; 3,4 – воздуховод подвода теплоты к стоянке автомобильной техники; 5,15 – воздуховод подвода теплоты к картеру масла ДВС; 6,16 – воздуховод подвода теплоты к картеру масла переднего моста ПМ; 7,17 – воздуховод подвода теплоты к картеру масла коробки передач КП; 8,18 – воздуховод подвода теплоты к картеру масла среднего моста СМ; 9,19 – воздуховод подвода теплоты к картеру масла заднего моста ЗМ; 10 – двигатель внутреннего сгорания; 11 – передний мост; 12 – коробка передач; 13 – средний мост; 14 – задний мост.

Figure 1. The concept of heating engine oils and transmission elements: 1 – heat unit; 2 – the main artery supplying heat; 3,4 – duct heat supply to the Parking of automotive vehicles; 5,15 – duct heat supply to the crankcase oil of the internal combustion engine; 6,16 – duct heat supply to the crankcase oil of the front axle PM; 7,17 – duct heat supply to the crankcase oil transmission KP; for 8, 18 – air duct for supplying heat to the crankcase oil of the middle bridge CM; 9,19 – duct heat supply to the crankcase oil of the rear axle ZM; 10 – an internal combustion engine; 11 – rear axle; 12 – transmission; 13 – median bridge; 14 – rear axle.

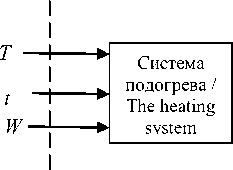
Рисунок 2. Факторы, влияющие на эксплуатационные и экологические показатели работы ДВС

*► ТДВС

> ТКП

^ ТГП

• Figure 2.    . Factors affecting the operational and environmental indicators of work ICE

В основу планирования эксперимента был заложен план полного факторного эксперимента (ПФЭ), в котором исследуемые факторы изменялись на двух уровнях: нижнем x ίн и верхнем x ίв , симметрично расположенных относительно основного уровня x ί 0 . [3]. Изображение плана ПФЭ при кодовом обозначении значений величин факторов показано на рисунке 3.

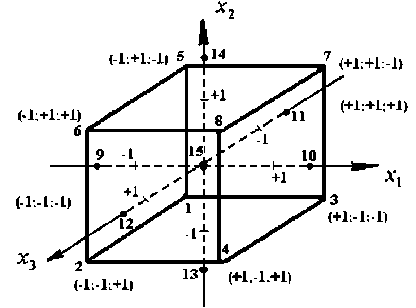
Рисунок 3. Графическое изображение ПФЭ

• Figure 3.    Graphic image of РРЕ

Построению плана ПФЭ предшествовало проведение ряда неформализованных действий (принятие решений), направленных на выбор локальной области факторного пространства, исходя из свойств исследуемого объекта.

Общее число опытов в плане для ПФЭ было равно:

N = NI + NII + NIII,          (1)

где NI = 2R = 8 – число всех возможных наблюдений; NII = 2R = 6, где R – количество факторов; NIII = 6; тогда N = 20, а плечо r = 2R/4 = 1,682.

Вначале выбираются основные (нулевые) уровни xί0, затем – интервалы варьирования ∆xί и определяются нижние xίн и верхние xίв уровни. В качестве исходной точки xί0 выбирали такую, которая соответствовала наилучшим условиям, определенным на основе анализа априорной информации о системе. На выбор интервала варьирования ∆xί накладывались естественные ограничения снизу (интервал не мог быть меньше ошибки фиксирования уровня фактора, так как в противном случае верхний и нижний уровни оказались бы неразличимыми) и сверху (верхний и нижний уровни не должны выходить за область определения).

Предельные значения входных (управляемых) факторов (таблица 1) устанавливаются в результате проведения предварительных опытов и анализа, выполненных ранее работ.

Уровни выходных факторов и интервалы варьирования отображены в таблице 2. Выбирая комбинации уровней факторов для каждой экспериментальной точки квадрата, получается план ПФЭ (таблица 3).

Таблица 1

Предельные значения входных (управляемых) факторов

Таblе 1

The limit values of the input (driven) factors

Факторы / Factors	Кодовое обозначение A coded indication	Обозначение Indication	Интервал варьирования The interval of variation	Уровни варьирования Levels of variation
				–1,682	–1	0	1	1,682
Температура окружающего воздуха, °C / Ambient temperature, ° C	x 1	т ов	10	–36	–29	–19	–9	–2
Время работы системы подогрева, мин / Working hours of the heating system, min	x 2	t	10	3	10	20	30	37
Мощность теплового агрегата, кВт / Power thermal unit, kW	x 3	w W Т . А .	20	12	20	40	60	74

Таблица 2

Уровни входных факторов и интервалы варьирования

Table 2

The levels of the input factors and ranges of variation

Входной (управляемый) фактор / Input (controlled) factor	Значение факторов / Meaning factors
	Нижнее / Lower x ίн	Верхнее / Top x ίв
т ов ,	-29	-9
t , мин	10	30
W ТА , кВт	20	60

Таблица 3

План полного факторного эксперимента ПФЭ

Table 3

Design of full factorial experiment PPE

	Кодированное обозначение / A coded indication			Натуральные величины / Natural values
	х1	х2	х3	Тов, °С	t, мин	WТА, кВт
1	-1	-1	-1	-29	10	20
2	-1	+1	-1	-29	30	20
3	+1	-1	-1	-9	10	20
4	+1	+1	-1	-9	30	20
5	-1	-1	+1	-29	10	60
6	-1	+1	+1	-29	30	60
7	+1	-1	+1	-9	10	60
8	+1	+1	+1	-9	30	60
9	-1,682	0	0	-36	20	40
10	+1,682	0	0	-2	20	40
11	0	-1,682	0	-19	3	40
12	0	+1,682	0	-19	37	40
13	0	0	-1,682	-19	20	12
14	0	0	+1,682	-19	20	74
15	0	0	0	-19	20	40
16	0	0	0	-19	20	40
17	0	0	0	-19	20	40
18	0	0	0	-19	20	40
19	0	0	0	-19	20	40
20	0	0	0	-19	20	40

Предполагается влияние трех количественных факторов ( R = 3) x ί ( ί = 1, R ) на некоторую реакцию у u в отведенной для экспериментирования локальной области факторного пространства, предельные значения. Тогда математической моделью влияния внешних воздействий на температурные показатели масел ДВС и элементов трансмиссии будут соотношения вида:

У де = L ( х 1 , х 2 , х 3 ) ;

У сО = ^fm ( х 1 , х 2 , х 3 ) ;             ⁽²⁾

у СН = f! ^{( х} 1 , х 2 , х 3 ^).

Допускается, что каждую из функций (2) можно с допустимой степенью точности представить в виде полинома второй степени от трех переменных, который содержит десять коэффициентов. Тогда каждая из функций у gе , у СО , у СН будут иметь вид [3]:

у=b + 52 Ьл +52 biX xi +52 ьих2,(3)

О                 I I                I j I j l = 1             l ^ j где bо – свободный член уравнения, определяется при условии, что рассматриваемые факторы находятся на средних «нулевых» условиях; x – масштабированные значения факторов, которые определяют функцию и поддаются варьированию; ι, j – индексы факторов; bι – коэффициент при линейных членах; bιj – коэффициенты двухфакторных взаимодействий, показывающие как изменяется степень влияния одного фактора при изменении величины другого; bιi – коэффициенты при квадратичных членах.

После выбора модели планирования ПФЭ, изучаемого процесса определяем функции у = f ( x 1 , x 2 …, x R ) и её уравнения в отведенной для исследования области факторного пространства. При этом необходимо спланировать и провести эксперименты для оценки числовых значений коэффициентов этого уравнения. Основная задача планирования эксперимента получение максимального объема необходимой информации об объекте моделирования, заданном в виде алгоритма [3].

По результатам трёхфакторного эксперимента составляется уравнение регрессии, в котором помимо линейных членов присутствуют члены, учитывающие эффекты парных межфакторных взаимодействий. Уравнение регрессии второго порядка в 3 – факторном эксперименте имеет вид: y = b 0 +b 1 х 1 +b 2 х 2 +b 3 х 3 +b 12 х 1 х 2 + +b 13 x 1 x 3 +b 23 x 2 x 3 +b 11 x 1 ² +b 22 x 2 ² +b 33 x 3 ². (4)

План ПФЭ 23 даёт возможность рассчитать 10 коэффициентов. Коэффициенты при членах уравнения регрессии (4) для ПФЭ 23 рассчитываются по выражениям [3]:

N           R N - Niii b0 = a0 ZУи - a4 ZZ 4y, u=1              i=1 u =1

N—Niii b = a У x y i 1             iu u u =1

NI b = a,yx x y ; ij 2 iu ju u u =1

N - Niii            R N - Nm            N b = a2_ у x2 y + a y V x2 y - a Vy ii                     iu u 3iu u 4u

² u = 1                    i = 1 u = 1                   u = 1

где a 0 = 0,16634; a 1 = 0,07322; a 2 = 0,12500; a 3 = 0,00689; a 4 = 0,05679. При расчете коэффициентов уравнения были использованы средние результаты опытов (N), рассчитанные по достоверным результатам отдельных повторностей. Средняя оценка результата u-го опыта рассчитывалась по формуле:

1   mu y„ =—z yuk, mu k=1

где m u – число повторностей u -го опыта, m u = const = m = 3.

ПФЭ не является полностью ортогональ-N ными. Так как Z xuxju = 0 (i = 0 ^ R,j = 1 ^ R, i u =1

NN

* ^j ), то Z X o u < * 0 и Z x uA * 0. Поэтому u = 1                         u = 1

по результатам реализации плана ПФЭ оцениваются лишь линейные эффекты факторов b i и эффекты межфакторных взаимодействий b ij . Коэффициенты b 0 и b ii коррелированны между собой, что усложняло процедуру вычислений этих коэффициентов и статистического анализа их значимости. Статистический анализ коэффициентов уравнений регрессии, описывающих процесс подогрева масел двигателя и элементов трансмиссии системой подогрева

Определение выхода процесса и обеспечение заданного уровня факторов в каждом опыте осуществлялись с ошибкой. Следовательно, с этой ошибкой определялись и коэффициенты уравнения регрессии.

Для того, чтобы показать с заранее заданной вероятностью Р, что полученные оценки коэффициентов уравнения по модулю либо больше (тогда они значимо отличаются от нуля), либо меньше ошибки в их определении (тогда они незначимо отличаются от нуля и должны быть из уравнения исключены) был проведен статистический анализ уравнения.

Определение построчной оценки дисперсии воспроизводимости единичного результата измерения в каждом опыте осуществлялось по формуле:

S ²( y uk ) =

m

Z ( y uk - y u )²

k=1__________________ m -1

Если измеряемая случайная величина у _uk распределена по нормальному закону во всем исследованном диапазоне, то независимо от значений y u дисперсия ст ² не будет изменять своей величины. Следовательно, оценки этой дисперсии должны быть однородными (являющимися оценкой одного и того же параметра, в данном случае - дисперсии ст ²).

Так как m u = m = const , то однородность оценок дисперсий анализировалась при помощи критерия Кохрена G :

_С   [ ' ² ( У -k ) ] max

G =              ,

Z S ² ( У uk )

u = 1

где [ S ² ( у _U k ) ]    - максимальная дисперсия;

N

Z S ² ( У _uk ) - сумма всех дисперсий.

u = 1

Далее сравнивалось это отношение с критическим значением критерия Кохрена G_кр . Если G <  G_Kp , то оценки однородны.

Критическое значение критерия Кохрена находилось по таблицам [1] в зависимости от числа степеней свободы числителя f 1 , числа сравниваемых дисперсий N и принятого уровня значимости q = 0,05.

Средняя для всего эксперимента оценка дисперсии воспроизводимости единичного результата рассчитывалась по формуле:

Us ² ( y „)

S ²( y_k ) =      ,-----

Nm

Z Z ( y uk - y u )²

u = 1 k = 1 __________________

N ( m - 1)

. (9)

Величина yu определялась по m повторностям, следовательно, она была ближе к истинному значению выхода, чем результаты единичных повторностей в соответствующем варианте опыта. Средняя для всего эксперимента дисперсия воспроизводимости среднего значения выхода в каждой строке была в m раз меньше дисперсии S(yk), т. е.:

S - ( .У ) = S"' m

Nm

Z I ( у* - у )²

и =1 к =1 __________________

N ( m - 1) m

В определении оценки любого из коэффициентов уравнения участвовали все N средних результатов опытов, оценкой дисперсии которых была одна и та же величина S ² ( у ), т. е. оценка дисперсии любого из независимо определяемых коэффициентов имела одну и ту же величину.

Структура формул для определения оценок коэффициентов была одинаковой со структурой формулы для расчета среднеарифметического:

Nm

7      У У ( у к - У ) ²

о2/—\     / j / j V ^у ик ^уи '

S ²( b ) = S -^ = - u ^L- k ^i---------- (11)

N     N ( m - 1) mN

Доверительная ошибка коэффициентов e(b i ) рассчитывалась по критерию Стьюдента t(P;f :

£ ( b i ) = t ( P ; f )( S ( b i )), (12)

где S( b i ) = S ²( b i ) - оценка коэффициентов уравнения регрессии.

Полученные коэффициенты регрессии bi- сравнивались с доверительной ошибкой e(b i ) . Если | b i . | >  е (b_t ), то оценка коэффициента b i значимо отличалась от нуля. В противном случае оценка b i считалась значимо, не отличающейся от нуля и приравнивалась нулю.

При получении незначительного линейного коэффициента какого-либо фактора искалось этому объяснение, проанализировав следующие ситуации:

─ данный фактор на исследуемый процесс не влияет;

─ выбран слишком малый интервал варьирования, в связи, с чем изменение выхода процесса, обусловленное изменением фактора, соразмерно случайным отклонениям, вызываемым влиянием неучтенных факторов или погрешностью измерительных приборов;

─ значение данного фактора в центральной точке эксперимента соответствует его оптимальной величине, в связи, с чем одинаковое его уменьшение или увеличение на Ах , - понизит выход процесса приблизительно на одну и ту же величину.

Если в уравнении после проверки значимости коэффициентов оставались все N коэффициентов, то проверка адекватности уравнения теряла смысл. Рассчитанный по такому уравнению выход процесса для условий какого-либо u-го опыта должен в пределах точности округления совпадать с величиной y i , принятой к расчету.

Если число значимых коэффициентов хотя бы на единицу было меньше числа опытов, то возникала необходимость (и возможность) статистической проверки адекватности уравнения экспериментальным данным.

Проверка адекватности (соответствия) математической модели экспериментальным данным осуществляется по критерию Фишера - F , которое сравнивалось с табличным значением критерия Фишера - F _г:

V2

f = s^ ⁽ F t ( р ^; f ^; f ^!). (13)

Для этого:

• —    рассчитывался выход у_и для каждого варианта опыта по уравнению, из которого исключены незначимые члены;

• —    находилась разность | у_и - у_и |;

─ рассчитывалась дисперсия неадекватности по формуле:

S

ад

N

ZI у и - Уи Г и =1________________

N - N'

где N' - число значимых коэффициентов в уравнении регрессии. Рассчитывалось F - отношение по формуле:

F =

s

S ²( У )

Сравнивалось полученное значение F-отношения с табличным значением F т ( P; f . ; f 2 ) критерия Фишера при степенях свободы f = N ( m - 1) и f 2 = N - N' .

В случае F <  F т. гипотеза об адекватности представления результатов эксперимента линейным уравнением регрессии принималась. Если F > F т , то уравнение неадекватно описывало экспериментальные данные, точность описания процесса данным уравнением значительно ниже той точности, с которой получены экспериментальные результаты.

На практике часто оказывается, что линейное уравнение регрессии адекватно описывает опытные данные, поставленные в точках плана, но неудовлетворительно характеризует внутреннюю область изучаемого факторного пространства. Если дополнительно к плану поставить в нескольких повторностях (m0) опыт в центре эксперимента, то, не приступая даже к расчету всех (кроме b0) оценок коэффициентов уравнения, можно судить о возможности описания процесса уравнением без включения в него квадратичных членов.

Оценкой суммарного квадратичного эффекта факторов являлась разность:

n

I У 0 ^- b o| = Ё b ii .              ⁽¹⁶⁾

к = 1

Если эта разность при заданной вероятно- сти значима, то осуществляется переход к планам второго порядка, позволяющим получить квадратичное уравнение процесса. Значимость разности (y0o -bo) устанавливалась при помощи определения доверительной ошибки этой разности: f(yo - bo) = t(P; f)S(yoo - bo) (17) и сравнивалась она с величиной этой разности.

Процедура такой проверки основывалась на дисперсионном анализе, осуществляемом в следующем порядке:

Рассчитывалась среднеарифметическая оценка результата опыта в центре эксперимента:

1 m ₀

л =— L У ки , m к = i

Рассчитываем оценку дисперсии:

S 2 ( У o к ) =

m

L ( У к o - к ) 2

к =1 __________________

⁽ m o ^- 1)

Находилась оценка дисперсии среднего результата, полученного в центре плана по формуле:

S ²( У ) = S^¹ .        (2O)

Находилась оценка дисперсии коэффициента b 0 :

s 4 b ) = ^S ">  = S^ ⁰ N mN

.

В соответствии с законом накопления ошибок записывалось:

Если оценки S ² ( y _{0 k} ) и S ² ( y_k ) однородны, то средневзвешенная оценка дисперсии единичного результата определялась по формуле:

.2 _ S ²( У O к )( m O - 1) + S ²( У к ) N ( m - 1)

S =------------------------------ (23)

( m _o - 1) + N ( m - 1)

которая может быть получена с числом степеней свободы f = ( m _o - 1) + N ( m - 1).

На завершающем этапе рассчитываем по формуле:

s ²( У - b o ) = s²

m ₀ Nm

= S 2 Nm + m o

Nmm ₀

.

Доверительная ошибка разности

( У o - b o ) Равна:

_£ (y_u - b o ) = t ( P ; f ) S ( У и - b o ).     (25)

Если e (У - b _o ) > | У_и - b _o)| , то квадратичные эффекты в уравнении не представлялись. Лишь в случае, если N >  N ' , представляется возможным судить об адекватности уравнения, рассчитывая F-отношение.

Если _£(У - b _o ) < | У_и - b _o )|, то с заданной вероятностью Р считаем эту разность значимой, следовательно невозможно по результатам реализации плана ПФЭ 2^R получить хорошую математическую модель процесса. Проведенные эксперименты показали, что данное неравенство выполняется, поэтому необходимо вывести уравнение регрессии второго порядка.

Используя метод наименьших квадратов и закон накопления ошибок, дисперсия коэффициентов регрессии рассчитывается по зависимости:

N

I У х² I I / J ^Х и I

S ²( b ) = к ^и = 1    7 s ²( У ),        (26)

А

I где      x2  – алгебраическое дополнение

• < ^iu 7

N диагонального элемента L х2 в определителе и=1

системы нормальных уравнений Δ; S ²( y ) – оценка дисперсии воспроизводи-мости результатов опыта.

Так как план эксперимента осуществляется в m повторностях, то в формулу (7) войдет средняя оценка дисперсии среднего результата:

Nm

XX ( y uk - у ) 2

• 5 ²( У ) = u^ ---п--     (27)

N ( m - 1)

с числом степеней свободы f = N ( m -1). Тогда:

5 ²( b о ) = а о 5 ²( у ),

5 ²( b/) = a i 5 ²( у ),

5 ²( Ъ_у ) = а ₂ 5 ²( у),

5 ²( Ъ „) = а з 5 ²( у ).

Окончательно для ПФЭ 2³:

5 ²( b i ) = 0,07322 5 ²( у ),

5 ²( bj_} ) = 0,125 5 ²( у), .         (28)

5 ²( b„) = 0,0597 5 ²( у )