Математическое моделирование возможных механизмов образования горячих точек

Известно, что для замыкания математических моделей многокомпонентных гетерогенных сред [1-5] необходимо определить выражения для интенсивности обмена, массой, импульсом и энергией между компонентами и фазами смеси. Данные соотношения могут быть получены только в результате детального рассмотрения механизма взаимодействия между компонентами и фазами. Данная работа, посвящена математическому моделированию возможных механизмов образования горячих точек при инициировании быстропротекающих процессов в гетерогенных взрывчатых веществах (ВВ).

В настоящее время принято считать, что под действием инициирующей ударной волны на разрывах сплошности внутри гетерогенного ВВ возникают горячие точки, протекание реакции в которых способствует усилению ударной волны. Это приводит к тому, что в гетерогенных В В детонация возбуждается легче, чем в гомогенных [6,7].

В соответствии с принятыми в настоящее время представлениями процесс инициирования детонации в гетерогенных В В проходит следующие стадии [7]:

• -    инициирование реакций в некоторой области В В (горячей точке);

• -    ускорение реакций горения и переход в детонацию с малой скоростью;

• -    переход детонации с малой скоростью в режим нормальной детонации.

КРАТКИЕ СООБЩЕНИЯ

В общем случае теория очагового инициирования ВВ (образования горячих точек) должна ответить на два независимых вопроса [8]:

• 1)    каковы причины появления очага разогрева при механическом воздействии на ВВ;

• 2)    какими критическими параметрами (температура, размер, длительность существования) следует характеризовать горячую точку, которая приводит к взрыву ВВ.

При ответе на первый вопрос К. Юханссон и П. Персон [9] показали, что если в сжатом газовом включении появляются мельчайшие капельки или насыщенные пары ВВ, то их воспламенение может явиться причиной взрыва, поскольку микрочастицы способны прогреться за время схлопывания пузырька газа.

Для подтверждения этого предположения в настоящей работе была решена задача о выходе ударной волны на свободную поверхность и проведен анализ возможности нарушения сплошности конденсированного В В вблизи данной поверхности.

• 1. О нарушении сплошности

Покажем, что при распространении ударной волны (УВ) в пузырьковой жидкости, в областях около поверхности пузырька может наблюдаться нарушение сплошности в жидкой фазе. Это связано с большим градиентом давления на границе « жидкость-газ », что приводит к увеличению скорости жидкой фазы в приповерхностном слое, и как следствие отрыв и образование отдельных капель В В около поверхности.

Для оценки данного явления рассмотрим задачу, моделирующую выход УВ на свободную поверхность (рис. 1) со следующими начальными условиями:

P 10 = 4 , 66 • 109 Па , р 10 = 1662 , 1 кгД 13 , и ю = 944 зi / c ,

P 20 = 1 , 045 • 105 Па , р ₂₀ = 1 , 2249 кгДi³ , и ₂₀ = 0 зi / c , индексом « 1 » обозначены величины относящиеся к жидкой фазе, индексом « 2 » - к газовой.

Рис. 1. Схема расчетной области

Для описания движения сплошной среды запишем законы сохранения массы, импульса и энергии для плоского одномерного случая в лагранжевых координатах:

dv 1    v ди 1    п   ди 1 f v д п "Ж-- V 10 Ж  = 0 ,  ЖЖ + V 1033— = ∂t     ∂m      ∂t     ∂m + дТ = 0 , P 1 = P 1 ( V 1 ,E 1) , ∂t ∂m	0 ,	(1)
Вестник ЮУрГУ. Серия « Математическое моделирование и программирование » (Вестник ЮУрГУ ММП). 2018. Т. 11, № 4. С.	154-160	155

Ф.Г. Магазов, Е.С. Шестаковская где V1 ,и 1, E1, Pi,т- удельный объем, скорость, удельная внутренняя энергия, давление и лагранжева массовая координата соответственно, P1 = P1 (V1, E 1) - уравнение состояния жидкого ВВ, П = P1 — ст, ст = 2дdm-, ст - тензор напряжений.

Конкретный вид уравнения состояния определяется либо из опыта, либо находится, в некоторых частных случаях, методами статистической физики. Для конденсированных веществ в настоящее время наиболее широко разработаны полуэмпириче-ские методы построения уравнений состояния [10-13], основанные на представлении давления и внутренней энергии в виде суммы упругих (холодных) и тепловых состав ляющих

{

P 1 = P 1 х ( V 1) + P 1 т ( V 1 ,Т 1) ,

E 1 = E 1 х ( V 1) + 3 NkT 1 ,

где N - число атомов в грамме, к - постоянная Больцмана, T 1 - температура ВВ.

Тепловые составляющие давления и внутренней энергии конденсированного вещества связаны между собой следующим образом:

{

P 1 т = Г( V 1) .   = Г( V 1) ET,

E, т = Cv T,, где Г - коэффициент Грюнайзена, характеризующий отношение давления к тепловой энергии решетки.

Для аналитического описания кривой холодного сжатия P 1 _х ( V ₁) часто пользуются интерполяционными формулами различного типа. В данной работе была использована широко распространенная формула Тета [6]

P 1 х = B 1

^V V ¹ 1 ⁰

-

Внутренняя энергия холодного сжатия тогда определяется уравнением

E 1 X

V 1

^— / P 1 х ^dV 1 = B 1 ^V 10

V 10

-

1+- к

V 10 J

Используя Грюнайзена

соотношения (2) и (3), получим уравнение

состояния в форме Ми -

E 1 = E 1 х ⁺ .1 ^{( P — Р} х ) = B 1 V 0

Г1

-

-

B 1 V 1

Г1

V _V 0 ₁

-

1+

PV 1

Г1 ■

Неизвестные B ₁ , n определяются из условия совпадения теоретической ударной адиабаты конденсированного вещества с экспериментальной адиабатой [14].

Для численного решения системы (1) использован метод Неймана - Рихтмайера [15], в котором использовалась искусственная диссипация (вязкость) из работы [16]. С учетом этого в исходной системе уравнений П заменяется на П = П + q, где величина q является искусственной вязкостью qm = — dp 10 unnm +1 — unm) (ст 1 a0 + ст2 | unm+1 — unm |) ,

КРАТКИЕ СООБЩЕНИЯ

δ =

0 , u 1 ⁿm +1 - u 1 ⁿm ≥ 0 ,

nn

^, u 1 m +1    u 1 m

< 0 .

На границе «жидкость-газ» используется условие в виде u1n+1 =u1n- dt · (P20 - P1n).

0 , 5 · h

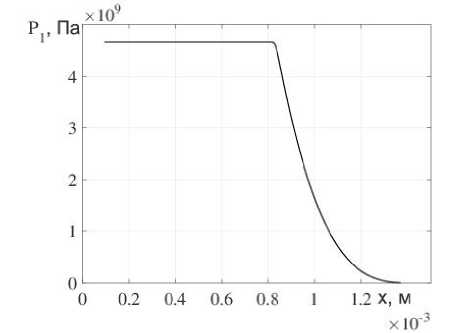
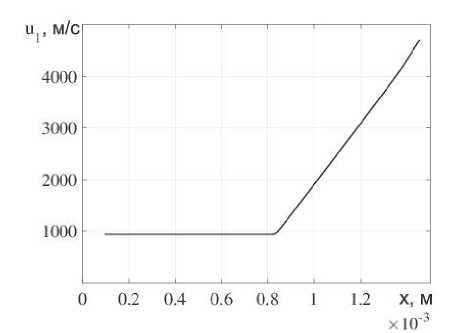
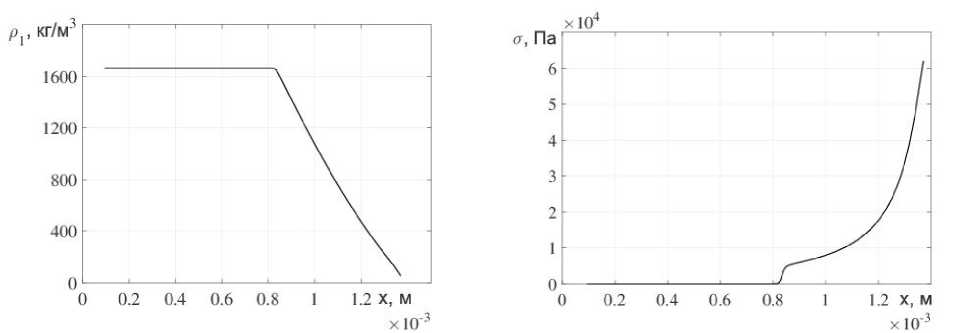
Расчеты проводились для жидкого ВВ, близкого по характеристикам к глицерину с р 10 = 1261 кгД I³. B 1 = 0 , 18. n = 5 , 45 . Г1 = 1 , 4. ц = 1 , 48 Па - с в об ласти L = 1 мм. На рис. 2 (а - d) представлены зависимости давления, скорости, плотности и тензора напряжений от координаты на момент времени t = 0 , 1 мкс.

Анализ результатов, представленных на рис. 2, показывает, что после выхода У В на свободную поверхность в конденсированное вещество начинает распространяться интенсивная волна разрежения. Это приводит к тому, что в конденсированном веществе падает давление и сильно возрастает напряжение. В силу того, что всякое конденсированное вещество обладает пределом прочности, то в веществе вблизи свободной поверхности может появиться нарушение сплошности материала, которое приведет к появлению отдельной микрочастицы.

(а)                                                       (Ь)

(с)                                                       (d)

Рис. 2. Зависимости давления (а), скорости (Ь), плотности (с) и тензора напряжений (d) от координаты

Ф.Г. Магазов, Е.С. Шестаковская

Результаты, приведенные в работе, подтверждают предположение К. Юханссона и П. Персона [9] о возможности появления мельчайших капелек ВВ, способных прогреться и воспламениться за время схлопывания пузырька газа.

Статья выполнена при поддерсяске Правительства РФ (Постановление № 211 от 16.03.2013 г.), соглашение № 02.А03.21.0011.