Математическое моделирование взаимодействия хищников и жертв

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 577.3.01(0.75)                                 

Взаимодействие типа хищник-жертва возникло давно. Эволюция хищников и жертв взаимосвязана: у хищника вырабатывались эффективные средства нападения, а у жертв — защиты. У хищников изменялась база трофического ресурса, а жертвы могли «уйти» от некоторых видов хищника, и стать жертвами других. При взаимодействии друг с другом происходила и гибель некоторых видов, как жертв, так и хищников.

Математические модели хищник-жертва учитывают, как правило, парные взаимодействия 1-2 видов хищников и жертв [1, 2].

Одна из первых моделей Лотки-Вольтерра учитывала взаимодействие один хищник - одна жертва, и предсказывала колебания численности обоих видов [2, 3]. В дальнейшем были разработаны модели, учитывающие различных факторы присущие реальным взаимодействиям с учетом влияния внешних факторов и пространственных распределений, миграционных характеристик [4].

В работе прорабатывается вариант взаимодействия нескольких видов хищников и нескольких видов жертв. Система считается свободно распределенной [5], замкнутой — миграция с сопредельных территорий не учитывается [6], образованием внутренних структур и диффузионными процессами пренебрегается [7-9].

Математическая модель

Модель Вольтерра [1] одна из первых объясняет временную цикличность численностей жертв и хищников. В модели в отсутствие хищника численность жертвы неограниченно растет. Введение внутривидовых потерь у жертв в модель Вольтерра в варианте, предложенном в [2, 3], приводит к модели из двух уравнений:

du

— = ^u (1 - u - av), dv dt

-yv(1 - в),

где u — численность жертвы, v — численность хищника, ^ — удельная скорость роста численности жертв, параметры у , a , в характеризуют скорости изменения численности особей.

Тривиальная точка притяжения системы уравнений (1) и = 0 и v = 0 является неустойчивой, а точка и = 1 и v = 0 будет устойчивой при выполнении условия в <  1 •

Третья неподвижная точка:

_           1 (     1

и = 1/в и v = — 1-- a

условия в >  1 , и будет устойчивой, поскольку корни

существует при выполнении характеристического полинома:

А2 + ^А + уи(1 - - V 0

матрицы Якоби правой части уравнений (1) в этой точке лежат в левой части комплексной плоскости.

Условия при t = 0 u = 1 и v = s , предполагают, что в начальный момент времени с жертвой начинает взаимодействовать малое количество хищников. Этим учитывается тот факт, что хищник не может появиться прежде жертвы.

Жертва проходит в процессе эволюции специализацию, имеет то преимущество, что отсутствует специфический для нее хищник. Соответственно модель (1) допускает существование жертвы как одиночной популяции, и гибель хищника в случае малой скорости его размножения.

Жертва – два хищника

Такая модель с учетом (1) представлена системой трех уравнений:

du

— = р и ( 1 - u - a v — a ^v2) ,

dv- = —/ivi(1 - Ри), dt

dvr = -/2v 2(1 - Au), dt

где v и v численности хищников.

Неподвижными точками уравнений (2) могут быть или

1           1    1

1. u 1 = 1/ в , v = — 1--, v ₂ = 0 ,

или

a

Л 1 L

2. u₂ = 1/ в , v = 0 , v ₂ = — 1 a

1 i

в2 у

То есть один из хищников должен погибнуть.

Для первой точки собственные значения матрицы Якоби

(  1Л

• *1 = Y 1 - в2 ,

к    в1 у

*=-рщ+J(pu )2 - щрк v,* = -pu - J(pu )2 - aPYvi

будут иметь отрицательные вещественные части при выполнении неравенств в > в •

Вторая стационарная точка будет реализовываться, если в >  в •

Таким образом, из двух хищников в модели (2) выживает тот, у которого на воспроизводства потомства требуется меньшее количество жертв.

Две жертвы и один хищник

Модель две жертвы и один хищник представлена системой трех уравнений

du

—1 = ^ u (1 - u - a v), t du

--2 = ^2u2 (1 - u2 - av), dt dv = -Yv(1 - ^1U1 - ^2u2) dt где u и u — численности жертв, v — численность хищника.

Вселение хищника в зону установившегося проживания будущих жертв соответствует неподвижная точка

щ = 1, u2 = 1, v = 0.

Характеристическими значения матрицы Якоби в этой неподвижной точке будут

Эта точка будет неустойчивой, если выполняется неравенство

• 1    < в+в.

Последнее неравенство соответствует требованию высокой скорости переработки жертв хищником, является условием выживания малочисленного хищника.

Координаты точки системы уравнений (3), в которой совместно существуют и жертвы и хищник

в+в -1

V =   --222----, и = 1 - a v, u = 1 - а v .

ва+ва

Эта неподвижнаяя точка реализуется при одновременном выполнении неравенств

в + в > 1,  а v < 1,  а2 v < 1.

В этой модели при выполнении первого неравенства хищник не погибает, а одна из жертв может погибнуть при некоторых значениях параметров, входящих в систему уравнений (3).

Сообщества

Эволюция живого мира сопровождалась постоянным появлением новых видов и гибелью уже существовавших. У хищников изменялся трофический ресурс. Специализация хищников к каждой жертве начинается, когда жертва становится специализированной, набирает достаточную численность и биомассу. Постепенно трофический ресурс хищников расширяется, а жертвы становится трофическим ресурсом различных хищников. В результате формируется сообщество хищников и сообщество их жертв.

Пусть n различных видов жертв являются трофическим ресурсом для m различных видов хищников. Пусть их парные взаимоотношения описываются системой уравнений (1). С учетом этого модель одновременного взаимодействия всех хищников и всех жертв принимает вид ( i = 1,2,..., n , j = 1,2,..., m ):

du       ,

—i- = uu 1 - u.

dt         ¹ i          i

m

—Z“sv,,

J=1J

dv dt

^— Y j^Vj

n

1 —Zji к      i=1

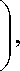
где u - численность i -ой жертвы ( i = 1,2,..., n ), Vj — численность j -ого хищника ( j = 1,2,..., m ), щ — удельные скорости роста численности жертв, Yj — удельные скорость гибели хищников, а — параметр, характеризующий скорость уничтожения i -ой жертвы j -м хищником, в/i — параметр, характеризующий скорость размножения j -го хищника при «поедании» i -й жертвы.

К системе уравнений (4) добавляются начальные условия при t = 0 :

Ui = 1 (i = 1,2,...,n) и Vj = sj (sj. □ 1) (j = 1,2,...,m).

В отсутствие хищников ( Vj = 0 , j = 1,2,..., m ) жертвы не взаимодействуют между собой, представляют собой изолированные популяции с неустойчивой тривиальной неподвижной точкой, и устойчивой точкой U = 1 ( i = 1,2,..., n ).

В неподвижной точке u _;. = 1 ( i = 1,2,..., n ) и Vj = 0 ( j = 1,2,..., m ) скорость роста численности хищников описывается уравнениями:

dv dt

—

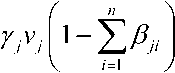
Соответственно для j -го хищника будет положительной, если выполняется условие:

n

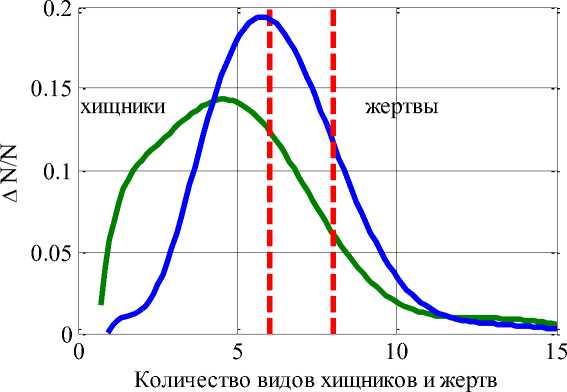
1

Как и для модели (1) для выживаемости малочисленной популяции хищника суммарная переработка j -м хищником всех жертв должна превышать пороговое значение, определяемое неравенством (5).

Нетривиальна стационарная точка системы уравнений (4) находится как решение системы линейных алгебраических уравнений (i = 1,2,...,n, j = 1,2,...,m):

m

^u_/+X^aj^v,= 1, j=1

n

Z ?,» = 1,

=1

или

( E a V u 1 X в oJkv , где α — матрица коэффициентов α размерности n× m, β — матрица коэффициентов β размерности m× n, E — единичная матрица размерности n× n, Ο — матрица размерности m× m, состоящая из нулей.

Физический смысл имеет решение системы уравнений (6) с положительными компонентами u и v . Отрицательные значения этих компонент можно рассматривать как ij

«гибель» хищников или жертв.

Численное решение системы уравнений (4) эффективно строится в среде математического пакета MatLab, в котором реализована векторизация вычислений, позволяющая сократить продолжительность вычислений. Имитационная модель основана на случайном выборе параметров модели (4) из заданного диапазона. Для случая N вариантов выбора параметров строятся вероятности распределений. Распределение хищников и их жертв строилось при случайном выборе параметров из диапазонов: ^е[1,3] ,

Y е [0.02,0.04], а е[1,2], в е[1,2]. На Рисунке для случая, когда в начальный момент в группу n = 20 жертв вселяется группа из m = 20 хищников, приведено распределение видов «выживших» хищников и жертв для N = 5000 . Вертикальными пунктирными линиями отмечены медианы распределений. Как следует из полученных результатов при взаимодействии хищников и жертв их общее количество уменьшается — часть видов не выживает.

Рисунок. Распределение выживших хищников и жертв

Заключение

Анализ результатов моделирования показал, что взаимодействие сообществ хищников и сообществ их жертв может сопровождаться гибелью отдельных групп как хищников, так и жертв. Сохранение начального количества видов и жертв в длительном эволюционном процессе маловероятно. Большие потери в видовом составе может понести сообщество хищников по сравнению с сообществом жертв. Разработанная модель сообществ отражает возможные вероятностные распределения для видов, существующих на ограниченной территории.