Математическое моделирование взаимодействия волн напряжений при взрыве системы зарядов, расположенных в ряд

Постановка задачи

Для решения задачи взрыва системы зарядов, расположенных по линии, применяется численный метод решения уравнений динамической теории упругости. Рассмотрим взаимодействие волн напряжений между смежными цилиндрическими зарядами (полостями) с соответствующими граничными условиями, т.е. как показано на рис. 1.

Рис. 1. Схема расположения цилиндрических зарядов

1 – цилиндрическая полость; 2 – ось симметрии между системами цилиндрических полостей; 3 – ось симметрии между двумя соседними (смежными) цилиндрическими полостями; 4 – ось симметрии между отбиваемым блоком и массивом горной породы; 5 – граница свободной поверхности.

Для численного решения данной задачи используются уравнения движения механики деформируемого твердого тела:

"' +      = d x d y

So y   STxy      a2 v(1)

+       = p2- a y    ax      a t2

а также обобщенный закон Гука и уравнения Коши:

Cx = ^S + 2MS, ;

ст,. = Xs + 2 ЦЕ v ;

Txy = 2 Msxy ;

dU    = dVdx ’ y dy

^S xy

1 f "U2 к 5y

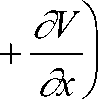
£ = Ex + Еу ,

где ox , oy - компоненты напряжений по осям X и Y; тху - касательное напряжение; U,V – компоненты вектора смещения по осям X и Y; t – время; р - плотность горной породы; А,ц - упругие константы Лямэ [1].

Граничные условия:

^o x ( x = r₀ =^— P ( t ) , ^o y ( y = r = ^— P ( t ) — на стенке зарядной камеры (пози-

P ( t ) - давление в за-

ция 1 на рис.1), где r0 – радиус зарядной полости, рядной полости;

^o y ( y = W = 0 , ^{Т х}У ⁽ у = W = 0 - на свободной поверхности (позиция 5 на рис.1);

dU             dU _ n _L

• —x— — U при x = 0, d x ^_ " ^ПР^И x = "2 - при взаимодей-

• ствии волн напряжений между смежными зарядными полостями, т.е. на оси симметрии (позиции 2, 3 на рис. 1), где L – расстояние между за-
• рядными полостями;

dV _ п

---= 0 при у = 0 - по линии расположения зарядов (позиция ^ У

• 4 на рис. 1).

Для решения уравнений гиперболического типа использовались разностные схемы типа «крест» с использованием нецентральной схемы Маккормака. Этот метод дает хорошие результаты при расчете движений сплошной среды, а динамический процесс интерференций волн напряжений близок к реальной картине.

В настоящее время подробно исследован вопрос для мгновенного создания давления в полости зарядной камеры, т. е. при стационарном давлении [2].

При взрыве в горной породе динамическая нагрузка внутри зарядной камеры, т.е. граничные условия с учетом изменения давления во времени, моделируется следующим образом:

0,

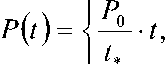
I Р о ,

t <  0

0 < t < t * t * < t < tk где t – текущее время; t* – время нарастания давления (оптимизирующий параметр); tk – конечное время; P0 – максимальное давление.

Результаты численного расчета напряженного состояния по линии расположения зарядов и в ортогональных направлениях представлены L при t* = 0, 3t1, 6t1, где ti =3—, c - скорость продольных волн в 2сp    p горной породе. На рис. 2 показаны эпюры растягивающих напряжений с областями разрушения законтурного массива (вокруг зарядных камер), где заштрихованными областями указаны зоны разрушения и жирными линиями показаны трещины.

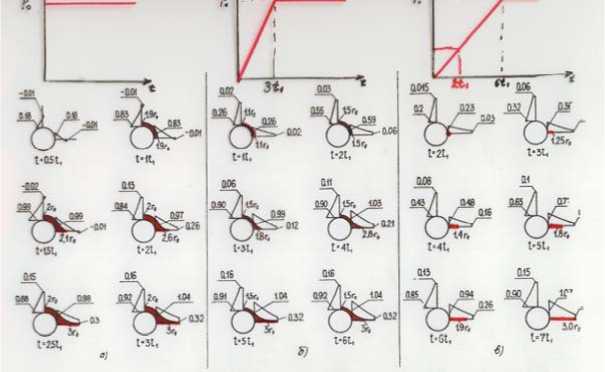
Рис. 2. Эпюры максимальных растягивающих напряжений P ₀

• а) t * = 0 ; б) t * = 3 t 1 ; в) t * = 6 t 1

На рис. 2а представлены результаты расчетов эпюр растягивающих напряжений при t * = 0 и при t <  t 1 симметричное распространение расходящихся цилиндрических волн напряжений вокруг зарядных полостей, а при t >  t 1 нарушается симметричность волн напряжений и образуется асимметрия. В результате интерференции волн напряжений между смежными зарядами формируется увеличение растягивающих напряжений по линии расположения, и при t >  3 t 1 уменьшается растягивающее напряжение в ортогональных направлениях, т.е. формируется перераспределение эпюр растягивающихся напряжений вокруг зарядных полостей.

При изменении формы импульса взрыва (рис. 2 б), когда время нарастания составляет t * = 3 t 1 , имеет место уменьшение главных компонент напряжений в ортогональных направлениях, проявляющееся при t >  3 t 1 некоторое снижение уровня напряжений в ортогональных направлениях и увеличение растягивающей компоненты напряжений по линии расположения зарядов. В этом случае наблюдается снижение разрушающего действия вокруг зарядных полостей и появляется возникновение асимметричных полей напряжений в меньшей степени.

Дальнейшее увеличение времени t * нарастания давления принципиально не меняет характера распределения напряжений (рис. 2 в), однако асимметрия поля напряжений проявляется в еще меньшей степени. При оптимизации динамических нагрузок необходимо появление эффекта зарождения (старт) радиальных трещин по линии расположения зарядов и тем самым увеличивается вероятность сохранности законтурного массива [3].

Численные результаты (рис. 2) подтверждают, что режим взрывного нагружения массива горных пород существенно влияет на процесс формирования динамического напряженно-деформированного состояния массива и результаты нарушенности законтурного массива представлены:

• -    по первой схеме - мгновенное взрывчатое превращение, т.е. когда давление выравнивается мгновенно во всем объеме зарядной камеры;

• -    по второй схеме - медленное взрывчатое превращение, связанное с кинетикой разложения, т.е. когда заряд взрывчатого вещества детонирует также мгновенно, но еще сказывается скорость нарастания давления продуктов взрыва в зарядной камере;

• -    по третьей схеме - имеет место еще более медленное взрывчатое превращение, чем в предыдущем случае. При этом процесс определяется кинетикой взрывчатого превращения.

Учитывая, что для крепких горных пород (гранит, мрамор) критические растягивающие напряжения в 10-12 раз меньше, чем критические сжимающие напряжения, то для сохранности законтурного массива необходимо, чтобы давление в зарядных камерах не превышало предела прочности на сжатие.

На рис. 3 представлены результаты модельных экспериментов, где показана качественная картина разрушения вокруг зарядных камер при различных воздействиях динамических нагрузок.

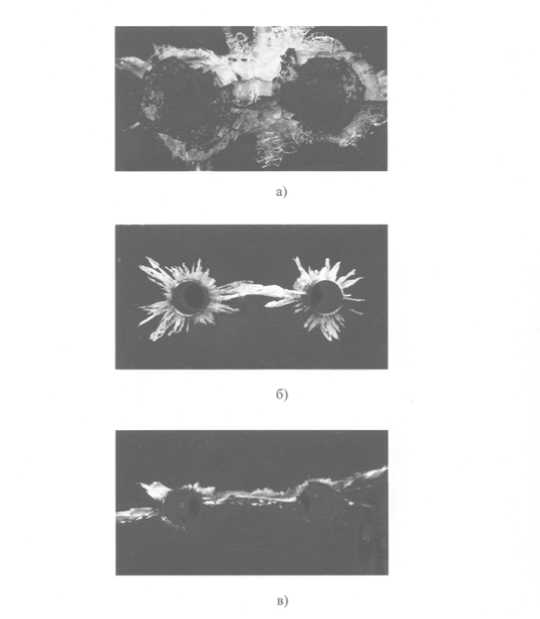
Рис. 3. Образцы после воздействия при различных режимах взрывного нагружения

На рис. 4 представлены натурные эксперименты добычи блочного

камня.

Рис. 4. Качественная картина добычи блочного камня

Основные результаты:

• 1)    показано, что асимметричное поле напряжений вокруг зарядных полостей формируется за счет взаимодействия волн напряжений между смежными зарядами и эффект увеличения растягивающихся напряжений по линии расположения зарядных камер;

• 2)    установлено, что при увеличении начальной фазы импульса взрыва в полости зарядных камер более вероятно проявляется эффект зарождения направленной радиальной трещины по линии расположения зарядов, т.е. за счет создания критической асимметрии растягивающих напряжений.

• 3)    демонстрируется технология щадящего взрывания модельных и натурных экспериментов, где показаны качественные результаты добычи строительных материалов.