Математическое моделирование: проблемы обучения в сельскохозяйственных вузах



'О 5

sol = О 10

(5 О

О 10^

15 О

0 °v

f(sol) =315.

Таким образом, с железнодорожного вокзала следует 10 туристов отвезти в отель «Уютный» и 5 туристов - в «Солнечный»; из аэропорта 10 туристов отвезти в отель «Солнечный» и 15 туристов - в отель «Слава»; туристов, прибывающих на морской вокзал, нужно отправить в отель «Морской». При этом суммарные транспортные расходы составят 315 руб. [2].

Использование электронных учебников позволяет сделать образовательный процесс более интересным, отвечающим реалиям сегодняшнего дня, увеличить скорость восприятия, понимания и глубину усвоения знаний, при этом не подразумевает отказа от обычных пособий - они могут с успехом дополнять друг друга. Кроме того, как показала практика, подобная форма очень привлекательна для студента своей новизной и нестандартностью, что тоже косвенно повышает качество обучения.

Литература

• 1.    Прикладные аспекты математики и математического образования: материалы III Междунар, науч. конф. «Математика. Образование. Культура», г. Тольятти ,17-21 аир. 2007 г. / под общ. ред. Р.А. Утеевой. Тольятти: ТГУ, 2007.

• 2.    Вуколов, Э.А. Основы статистического анализа: практикум по статистическим методам и исследованию операций с использованием пакетов Statistica и Excel / Э.А. Вуколов. М.: Инфра-М., 2004.

С.А. КАРТАШОВА (Чебоксары)

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ: ПРОБЛЕМЫ ОБУЧЕНИЯ В СЕЛЬСКОХОЗЯЙСТВЕННЫХ ВУЗАХ

Рассматриваются особенности преподавания курса «Математическое моделирование» в сельскохозяйственных вузах. Приведены описания лабораторных работ, разработанных по принципу нарастания сложности и с использованием решения «сквозных» задач.

Курс «Математическое моделирование» тесно связан со знанием персональных компьютеров (ПК) и прикладных программ. Лабораторные работы - это решение практических экономико-математических задач, составленных по данным конкретных хозяйств. Выбор программы для решения задачи делается самим студентом. Важное значение имеет экономический анализ результата решения на ПК. Здесь сливаются воедино теория и практика.

Говоря о проблеме преподавания курса «Математическое моделирование», следует отметить, что у студентов он вызывает проблемы, прежде всего, из-за слабой математической подготовки. Особенно это касается студентов агрономического факультета (у них при поступлении в вуз нет даже вступительного экзамена по математике). Необходимо также учесть, что курс «Математическое моделирование» преподается на 3 - 4-м курсах, когда о математике как таковой студенты вообще позабыли. Поэтому автор разработал данный курс в варианте «руководство по использованию». Для этого он применил два основных метода: принцип нарастания сложности и так называемые «сквозные» задачи, в которых исходные данные меняются в зависимости от изучаемого материала, чтобы студенты сразу обратили внимание, как при этом изменится решение самой задачи.

Потом ее решают несколькими методами с использованием различных программ. Студентам не нужно вникать в постановку новой задачи. Они просто исследуют сам метод решения, видят хорошие и плохие стороны метода. При этом формируется профессионализм в выборе нужного метода или программы для решения профессиональных задач.

Принцип нарастания сложности тоже очень важен. У студентов нет боязни сложных задач, т.к. сложность повышается постепенно, в зависимости от экономикоматематической модели. На первых порах, при ознакомлении с «математическим моделированием», предлагаются для решения простые модели, которые не требуют особой математической базы. Внимание студентов фиксируется только на решении задачи с помощью ПК. Потом модель расширяется и требуются большие знания, но студент к этому готов. У него не возникает отчуждения от предмета (из-за его сложности).

Приведем схему такого практического занятия:

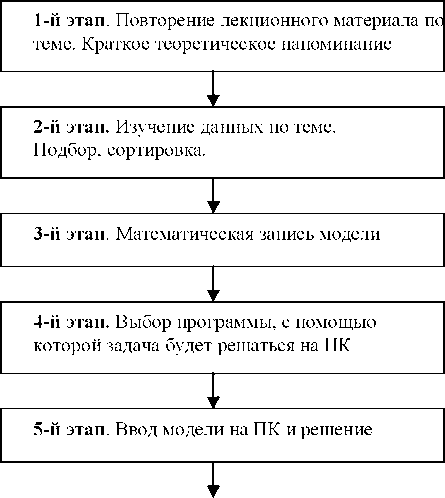
Автором разработаны и внедрены специальные лабораторные работы для каждого факультета, учитывающие их специфику, и на основе их сформировано содержание курса «Математическое моделирование» для различных групп специальностей ЧГСХА, в котором общие цели обучения моделированию получают конкретизацию в зависимости от требований профессиональной подготовки [4].

Проиллюстрируем лабораторные работы разной сложности на примере экономикоматематической модели по кормовому рациону. Первый вариант - для студентов агрономического факультета. Это более легкий вариант данной модели, т.к. не требует введения дополнительных переменных (по зоотехническим требованиям). Второй вариант - для студентов экономического факультета, где требуется введение всех типов перемени ых, что существенно усложняет решение. Все лабораторные работы выполняются с помощью программы ЛПГ, которая использует симплексный метод решения задач линейного программирования, или Excel.

Агрономический факультет

Лабораторная работа 1. Составление оптимального кормового рациона на ПК

Задание: составить экономико-математическую модель задачи и решить ее с помощью программы ЛПГ. Дать подробный экономический анализ решения.

Составить оптимальный суточный кормовой рацион на стойловый период для дойной коровы живым весом 400 - 450 кг с суточным удоем 16 кг при жирности 3,2%. Для обеспечения такой суточной продуктивности необходимо, чтобы в рационе коровы содержались следующие питательные вещества, не менее: кормовых единиц - 9,5 кг, переваримого протеина - 1005 г, кальция - 116 г, каротина - 514 мг и сухого вещества - не более 20 кг. В соответствии с зоотехническими требованиями отдельные группы кормов в рационе могут изменяться в следующих пределах: концентрированные корма - от 2 до 3 кг, сочные - от 15 до 20 кг, грубые корма от 12 до 20 кг и корнеклубнеплоды - от 2 до 8 кг. Кроме того, в группе грубых кормов солома должна составлять не более 25%. Критерий оптимальности - минимум себестоимости рациона (в руб.).

Содержание питательных веществ в кормах

Корма	Кормовые единицы, кг	Переваримый протеин, г	Кальций, г	Каротин, мг	Сухое вещество, кг	Себестомость, руб-
Комбикорм	0,9	112	15	0	0,87	14,5
Ячмень	1,21	81	1,2	1	0,87	8,2
Сено	0,42	48	6	15	0,85	3,4
Солома	0,31	14	4,3	4	0,85	0,2
Силос	0,2	14	1,5	15	0,26	0,6
Картофель	0,3	16	0,2	0	0,23	9,7
Свекла	0,12	9	0,4	0	0,13	2,1

Экономический факультет

Лабораторная работа 1. Составление задачи оптимального кормового рациона на ПК Задание: составить экономико-математическую модель задачи и решить ее с помощью программы ЛПГ. Дать подробный экономический анализ решения.

Составить оптимальный суточный кормовой рацион на стойловый период для дойной коровы живым весом 400 - 450 кг с суточным удоем 16 кг при жирности 3,2%. Для обеспечения такой суточной продуктивности необходимо, чтобы в рационе коровы содержались следующие питательные вещества, не менее: кормовых единиц - 9,5 кг, переваримого протеина - 1005 г, кальция - 116 г, каротина - 514 мг и сухого вещества -не более 20 кг. В соответствии с зоотехническими требованиями отдельные группы кормов в рационе могут изменяться в следующих пределах, в процентах к общему количеству кормовых единиц^-, концентраты - от 10 до 30, грубые - от 10 до 25, сочные -от 30 до 50, корнеклубнеплоды - от 6 до 15.

Кроме того, при составлении рациона необходимо учитывать ряд условий хозяйства, в соответствии с которыми удельный вес ячменя в группе концентрированных кормов должен составлять не более 30%, соломы в группе грубых - не более 25%, картофеля в группе корнеклубнеплодов — не менее 14%. Критерий оптимальности - минимум себестоимости рациона (в руб.). Для сбалансированности рациона по переваримому протеину предусматривается включение в него карбамида (не более 15% от общей потребности в протеине. Стоимость 1 кг карбамида составляет 6,6 коп., а 1 кг его эквивалентен 2600 г переваримого протеина.