Математическое обеспечение иерархического цифрового управления сложным технологическим объектом

Структура системы иерархического цифрового управления сложным технологическим объектом приведена на рис. 1.

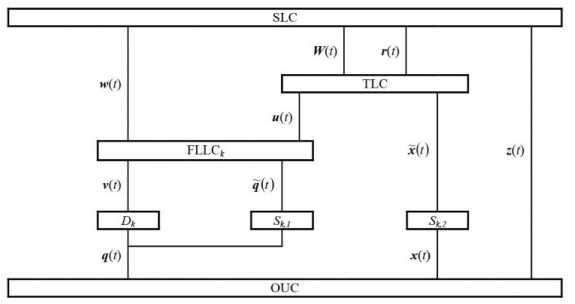
Рис. 1. Структура системы иерархического цифрового управления сложным технологическим объектом

В состав системы (рис. 1) входят: контроллер стратегического уровня (SLC-контроллер), контроллер тактического уровня (TLC-контроллер) и K контроллеров функционально-логического уровня (FLLCk-контроллеры, ке{1, ..., K} [19]. Разделение контроллеров по уровням может быть реальным или виртуальным. Например, SLC- и TLC-контроллеры могут быть реализованы на одной физической ЭВМ с виртуальным разделением по уровням, а FLLCк-контроллеры могут объединяться в группы, каждая из которых реализуется на одном физическом цифровом контроллере.

При управлении объектом (OUC) на каждом иерархическом уровне реализуется своя часть интегрального алгоритма управления.

На верхнем, стратегическом уровне формируется цель управления W ( t ) в виде развивающейся в физическом времени последовательности изменений вектора состояния OUC, x ( t ) = { x k ( t )}, которая обеспечивает, например выпуск возможно большего объема продукции в единицу времени, поддержание режима функционирования технологического оборудования, согласованное взаимодействие компонентов робототехнических систем и комплексов специального назначения и т. п. [20-24].

Из глобальной цели W ( t ) TLC-контроллер формирует вектор u ( t ) = { u k ( t )} текущих желаемых значений вектора x ( t ) состояний OUC, который передается на FLLC к -контроллеры. Кроме того, на эти контроллеры с выходов SLC-контроллера могут быть непосредственно переданы значения настроек w ( t ) параметров регуляторов, необходимые для реализации оптимальных режимов функционирования приводов D k с сенсорами S 1,k в контурах локальных обратных связей.

По вектору желаемых значений состояний u ( t ) и результатам измерений q ( t ) = [ q 1 ( t ) = { q k ( t )} [25, 26] с помощью сенсоров S 1,k физических перемещений q ( t )={ q k ( t )} приводов D k формируются воздействия на объект управления, которые приводят к изменению его состояния x ( t ). Результаты измерения в виде вектора x ( t ) = { x k ( t )} возвращаются на уровень TLC, обеспечивая обратную связь по регулируемым параметрам технологической установки. Кроме того, вектор [ u ( t ) ,x ( t ) ] = [ u 1 ( t ) , формируемый как объединение векторов u ( t ) и x ( t ) , возвращается в SLC для определения цели управления w ( t ) на следующем шаге функционирования системы.

Также на уровень SLC передаются элементы векторов z ( t ) = { z _k ( t )} и r ( t ) = { r _k ( t )}. Элементы вектора z ( t ) напрямую не используются в процессе управления, но дают дополнительную информацию о состоянии объекта, например, о температуре, давлении и влажности в приобъектной зоне, о срабатывании концевых выключателей, аварийных клапанов и т. п. Элементы вектора r ( t ) представляют собой логические переменные, которые несут информацию о результатах отработки системы предыдущего шага управления. Совместно элементы векторов x ( t ) , u ( t ), z ( t ), r ( t ) образуют пространство принятия решений в системе управления объектом OUC.

Математическое обеспечение алгоритмов, реализованных в контроллерах

SLC-, TLC- и FLLC _k -контроллеры работают по типовому циклическому алгоритму общего вида, показанному на рис. 2, а , состоящему из неисполнимых операторов a ₀(_a) «Начало» и a J(_a)+ 1 «Конец» и исполняемых операторов a j(_a), j g {1, ..., J }. Циклическим алгоритм делает обратная связь [ a J(_a)₊ 1 , a j(_a) ], показанная на рис. 2 пунктирной стрелкой.

Исполнимые операторы реализуют:

в алгоритме SLC-контроллера - функции ввода данных векторов x (t), u (t), z (t), r (t), расчет элементов вектора w (t) и передачу рассчитанных значений в TLC, расчет элементов вектора настроек w (t) параметров регуляторов и передачу рассчитанных значений в FLLCk- контроллеры;

в алгоритме TLC-контроллера - функции: ввода векторов x ( t ) и w ( t ), расчета и вывода в FLLC _k -контроллеры элементов u ( t ), расчета и возврата в SLC-контроллер элементов вектора r ( t );

в алгоритме каждого FLLC k -контроллера - функции ввода значений u _k и q _k , расчета и вы-

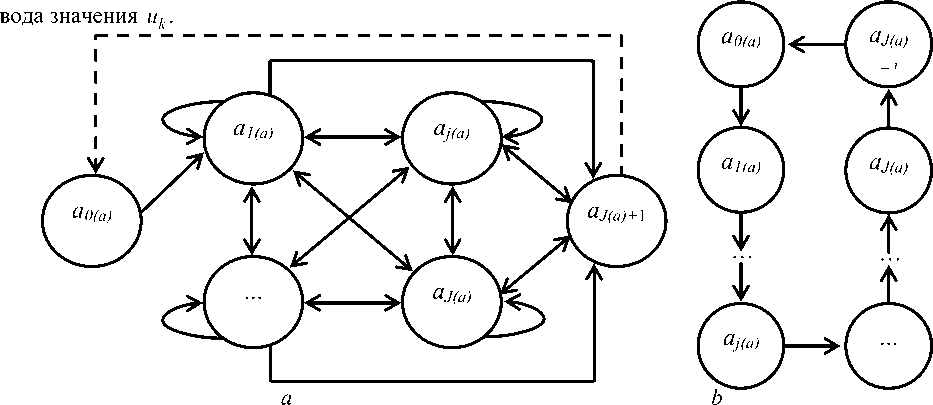
Рис. 2. Структура типового алгоритма контроллеров всех уровней: a – общего вида; b – линейно-циклического вида

Вследствие того, что SLC-, TLC- и FLLC k-контроллеры интерпретируют свои алгоритмы в реальном физическом времени t последовательно, оператор за оператором, между обращениями к внешним по отношению к рассматриваемому контроллеру устройствам естественным образом образуются временные интервалы (задержки) [27–29]. Наличие интервалов времени между тран- закциями, генерируемыми каждым контроллером, должно учитываться при проектировании программного обеспечения контроллеров системы. Универсальным подходом к оцениванию временных интервалов является построение полумарковской модели типового алгоритма [30-32]:

М = { A, h ( t ) } , где A = { a ₀(_a), a i(_a),... a ja), a _J(_a)₊ 1 } - множество состояний, совпадающее с множеством исполнимых и неисполнимых операторов; h ( t ) = ^ hj^ _n t_a^t ) ] = p ® f ( t ) - полумарковская матрица, описывающая временные и стохастические свойства алгоритма; p = ^ р^ _п(а) ] - стохастическая матрица; f ⁽ t ) = [ f ( a ) , „ ( a ) ⁽ t ) ] - матрица плотностей распределения времени пребывания процесса в состояниях множества А до переключения в сопряженные состояния, причем размерности всех матриц [ J ( a )+2] х [ J ( a )+2].

Полумарковская модель правильно синтезированного алгоритма обладает следующими свойствами:

для каждого состояния aj(a)gA существует хотя бы один путь а0^— ^а^ и хотя бы один путь а}(а) — aj(^+j, то есть полумарковский процесс при замкнутой обратной связи является возвратным;

вероятности переключения между состояниями a j(_a) удовлетворяют условиям

Математика

n

J ( a )

1, j ( a ) ^ J ( a ) + 1,

I   p j ( a ) n n ( a H

( a ) = 0 ( a )

or j ( a ) = J ( a ) + 1, feedback is closed;

0, j ( a ) = J ( a ) + 1, feedback is open;

на время пребывания в состояниях полумарковского процесса накладываются ограничения »

⁰ <  T j ( a ) , n ( a ) min ~ ^arg fj ( a ) , n ( a ) ⁽ t ) “ T j ( a ) , n ( a ) max ’ J ^fj' ( a ) , n ( a ) ⁽ t ) dt = ¹;

в модели алгоритма с замкнутой обратной связью [ J ( а )+1]-я строка полумарковской матрицы h ( t ) имеет вид ^ fJ ( a )_{+ 1} , ₀ ( a ) ( t ) ,..., 0,..., о ] , где f J ( a )_{+ 1} , ₀ ( a ) ( t ) - плотность распределения времени работы операционной системы контроллера по перезапуску исследуемого алгоритма.

Полумарковский процесс является возвратным, плотности распределения времени пребывания в его состояниях имеют область определения, локализованную в положительной полуплоскости, следовательно, процесс является эргодическим [30–32]. Плотность распределения времени возврата в состояние а о (а) полумарковского процесса ^ и среднее время периода равны соответственно

^

f c ( t ) = I 0 ( . ) L - I { L [ h ' ( t ) ] }^{

. ^= 1

»

I J (a )+1* fJ (a )+1,0( a)( t ) ; Tc = J tfc ( t ) dt , где fc (t) - плотность распределения времени от начала текущего цикла до начала следующего цикла работы программы; L [...], L [...] соответственно прямое и обратное преобразование Лапласа; I R(a) — [J(а )+2]-элементный вектор-строка, нулевой элемент которого равен единице, а остальные элементы равны нулю; I^+1 - [J(а)+2]-элементный вектор-столбец, последний,

[ J ( а )+1]-й элемент которого равен единице, а остальные элементы равны нулю; h ' ( t ) - полумар-ковский процесс, описывающий алгоритм с разомкнутой обратной связью, у которого [ J ( а )+1]-я строка имеет вид [0 , ..., 0]; * - обозначение операции свертки.

На структуру исследуемого алгоритма может быть дополнительно наложено следующее ограничение: в течение одного цикла каждый канал, связывающий один контроллер с другими контроллерами и периферийным оборудованием, опрашивается по одному разу, а, следовательно, исполнимые операторы a j(_a) образуют гамильтонов цикл на графе (см. рис. 2, а ).

Схема линейно-циклического алгоритма, представляющего один из возможных гамильтоновых циклов, приведена на рис. 2, b . Для полумарковского процесса с гамильтоновым циклом

J ( a ) + 1

f c ( t ) = f 0 ( a ) ( t ) * f a ) ( t ) *-* f j ( a ) ( t ) *-* J ( a ) ( t ) * J ( a ) . , ( t ) ; T c = I    TH a ) •

I ( a ) = 0 ( a )

где f^а^ (t) и T^ - плотность распределения и математическое ожидание времени пребывания полумарковского процесса в состоянии aj(a) гамильтонова цикла до его переключения в следующее состояние.

Математическое обеспечение обработки данных в FLLC _k- контроллере

Реализация полумарковской модели обработки данных на нижнем (функциональнологическом) уровне иерархии в системах с механизмами, в которых присутствует сухое трение, и естественное ограничение на скорость перемещения терминального элемента (руля, задвижки, клапана и т. п.), а также инерционность сенсора S _k, 1 , дает следующую систему дифференциальных уравнений третьего порядка в форме Коши:

" dqk ,i ( t )         (л

⁼ qk ,2 ⁽ t ;

< dqk2 (t) = -ak,1 • qk,2 - ak,2 • sgn [qk,2 (t )] + ak,3vk (t ), q^)=—ak ,4 qk(t)+qk ,i (t), где qk,1 (t) = qk (t) - физическое положение терминального элемента; qk - значение положения, измеренное сенсором Sk,1 ; qk,2 – скорость перемещения терминального элемента с учетом ограничения; ak2 • sgn [qk2 (t)] - сила сухого трения; ak,1 ^ ak,4 - коэффициенты, определяющие динамику и точность работы механизма исполнительного устройства и сенсора.

Величины   q k ,2   и   q k ,2   ^{связаны} соотношениями   q_k ,2 = q k ,2   при   q k ,2min ^ q k ,2 ^ q k ,2 m max ';

q k ,2 = q k ,2 min ^пр^и q k ,2 ^ q k ,2 min ; q k ,2 = q k ,2max ^пр^и q k ,2 ^ q k ,2max .

Наиболее часто на практике при обработке данных в FLLCk-контроллере применяется алгоритм пропорционально-интегрально-дифференцирующего (ПИД) регулятора [33, 34], который имеет вид vc, k ( t ) = aFL,P, k ( WP, k ) ' ^FL, k ( t ) + aFL,D, k ( wD, k ) X      .'     + aFL,In, k ( win, k ) ’J ^FL, k (f) dT;

I „ —                    0     ,

I / fl, k ( t ) = u k ( t )^- q k ( t ) ;

где / _fl , _k ( t ) - ошибка в установлении заданного положения q _k ( t ) терминального элемента; a _FL , _P , _k ( w _P , _k ) , a _FL , _D , _k ( w _D , _k ) , a _FIJn , _k ( w _In , _k ) - коэффициенты при пропорциональной, интегральной, дифференциальной составляющих соответственно, определяющие качество переходных процессов на FLLC _k -уровне; w c , _k =[ w _P , _k , w _D , _k , w _In , _k ] - вектор данных, вводимых в FLLC _k -контроллеры с SLC-контроллера для установления оптимальных режимов управления OUC.

Каждый FLLC k -контроллер является цифровым, поэтому производная и интеграл в алгоритме ПИД-регулятора определяются соответственно по формулам конечной разности и конечной суммы [35, 36], т. е.

d^r ( t )                                   n

----T----= ^ FL, k ( ⁿ ) ^- ^ FL, k ( ^{n -} 1 ) ; J ^ FL, k ( ^T ) d ^T = t ^f FL, k ( i ) , ^dt                                     0                  i = 0

где n - дискретное время, связанное с реальным физическим временем соотношением t = T c , _FL , _k n ; T _{c ,FL, k} – период опроса FLLC k - контроллеров.

Для вычисления производной каждый FLLC k -контроллер должен осуществить две транзакции с TLC-контроллером и две транзакции с сенсором S 1,k . Вследствие дополнительных ограничений, которые накладываются на алгоритмы обработки данных по гамильтонову циклу, на это необходимо затратить 2 T _{c ,TLC, k} единицы физического времени. Поэтому управляющее воздействие на выходе FLLC k -контроллера появляется с дополнительной задержкой по времени относительно момента поступления данных u _k ( t ) и q _k ( t ) , т. е.

^vk ⁽ t ) = vc , k ⁽ t - ^2Tc ,FL, k ) .

Накопление конечной суммы происходит в течение всех периодов работы контроллера и не оказывает существенного влияния на время чистого запаздывания в контуре обратной связи.

Математическое обеспечение обработки данных в TLC-контроллере

Объект управления, в котором TLC-контроллер обеспечивает заданный режим функционирования, в общем случае описывается системой нелинейных дифференциальных уравнений:

Математика

V k

, M      d m ⁽ x ' x ( t ' d M ¹ x ' x ( t '     1     d m ⁽ q ' q ( t '      d M ¹ q ¹ q ( t '

= 0, 1 <  k <  K ,

t ,x ⁽ t ' d m ( x '   ■-■   dt M ( x '   ^{,q (} t ' dt *'   ’-, d M ⁽ q '

где q ( t ) - вектор воздействий, формируемый на уровне FLLC _k - контроллеров; x ( t ) - вектор параметров состояния OUC, измеряемых сенсорами S _k,2 и вводимых в TLC-контроллер.

С целью унификации программного обеспечения при расчете элементов вектора u(t) применяется алгоритм ПИД-регулятора, который при отсутствии алгоритмически создаваемых перекрестных связей между каналами управления имеет вид uk ( t ' = aTLC,P,k

‘ ^ TLC, k ⁽ t ' + ^ TLC,D, k

d ^S TLC,k ⁽ t ' dt

t

+ ^a TLC,In, k * f ^ TLC, k ^{( т} ' d ^T ;

^LC,k (t ' = Wk (t'- xk (t' ,1 < k < K, где ^TLCk (t' - текущая ошибка установления заданного значения xk (t'; ^TLCPk, aTLC P k,

^TLc , P , k — коэффициенты передачи ПИД-регулятора по пропорциональной, дифференциальной и интегральной составляющим; Wk (t' - цель управления, определяемая на стратегическом уровне как желаемое значение регулируемого параметра xk (t'.

Производная и интеграл в алгоритме ПИД-регулятора также рассчитываются по формулам конечной разности и конечной суммы, поэтому между сигналами x (t) и u (t) возникает задержка по времени, равная 2Tc TLC k. Эта задержка может быть отнесена к сенсорам S2,k, поскольку пере- крестные связи между каналами на уровне алгоритма функционирования TLC-контроллера отсутствуют. С учетом задержек по времени модель преобразования сигналов x (t) сенсорами при- нимает вид dxk (t  2Tc tlc k'   ~ /              \            / \ aS,k, 1          ^           + xk ( t - 2Tc,TLC ,, k ' = aS ,k, 2 xk ( t ' , где aS,k,1 и aS,k,2 - параметры, определяющие быстродействие и коэффициент передачи S1,k и S2,k соответственно.

Кроме интервала 2T _{c TLC k} при работе TLC-контроллера возникает такое явление, как перекос данных. Без нарушения общности можно считать, что внутри гамильтонова цикла первой транзакцией является ввод элемента Х 1 ( t ' , после чего в порядке, определенном алгоритмом, вводятся оставшиеся элементы указанного вектора и выводятся элементы вектора v ( t ). Задержки по времени между началом ввода X 1 и началами ввода X ₂ , ..., x _k , ..., x _K порождают перекос данных T n,1 = ⁰, T n,2- , T n, k , -, T n, K при вводе. Задержки ^по времени   T out,i = о, T out,2 ,..., T out, k ,•.., T out, K ^ме"

жду началом вывода элемента v i вектора v ( t ) и началами выводов элементов v ₂ , ..., v _k , ..., v _K порождают перекос данных при выводе v ( t ). Временной интервал T _{del k}/ , алгоритмически формируемый между вводом x k и выводом v l , дает часть времени чистого запаздывания формирования l -го элемента вектора управления относительно к -го элемента вектора состояния. Полное время чистого запаздывания определяется порядком следования операторов в гамильтоновом цикле.

Вектор r (t) = {rk (t)} формируется как вектор подтверждения исполнения команды W(t). Элементы этого вектора обнуляются после передачи в SLC-контроллер и устанавливаются в единицу, если к началу следующей транзакции величина ошибки ^TLC k (t' = Wk (t' - xk (t' выполнения команды не превышает заданного порога, то есть rk =1 , when ^TLC, k (t' < ^TLC , k , где £tlc k - пороговое значение сигнала ошибки по к-му регулируемому параметру OUC, xk (t'.

Записанные выражения представляют собой полную модель функционирования TLC-контроллера в составе иерархической системы управления.

Математическое обеспечение обработки данных в SLC-контроллере

В SLC-контроллере (на стратегическом иерархическом уровне) реализуются алгоритмы, обеспечивающие эффективные режимы работы оборудования. Одна из возможных реализаций подобного алгоритма – это нейронная сеть, которая используется для настройки параметров управления FLLC k - контроллеров [3]. Настройка осуществляется по результатам наблюдения состояния OUC, TLC, D k . Для принятия решения о настройке параметры, описывающие указанные блоки иерархической системы, в виде векторов u ( t ), x ( t ), r ( t ) передаются с соответствующих уровней в SLC. Дополнительно к перечисленным на этот уровень передаются данные о нерегулируемых параметрах OUC, обозначенные на рис. 1 как вектор z ( t ). Все переданные данные образуют параметрическое пространство y = u u x и r и z = [ у ^ ^,..., у .^ ^,..., у^ ^] принятия решения. Решение заключается в установлении значений элементов векторов W ( t ) и w ( t ) , передаваемых на уровни TLC- и   FLLC k - контроллеров   соответственно. Вектор

Для выбора векторов W ( t ) и w ( t ) в нейронную сеть уровня SLC-контроллеров включаются нейроны, формирующие в пространстве параметров y систему из J ( c ) гиперплоскостей:

J ⁽ у )

X   bj(c), j(у)yj(у) = cj(c) ,1( c    J (c )< J ( c ), j (у )=>( у)

где b^j^ и c^_c^ - параметры j ( c ) -го нейрона, задаваемые при настройке нейронной сети.

При подстановке в систему уравнений   J(c)   гиперплоскостей вектора yt = y(t) = [у1(у),t,...,yj(у),t,...,yJ(у),t ' текущих оценок параметров формируются значения cj.(c),t правых частей линейных уравнений J(c) гиперплоскостей.

^{J (} у )

X    b j ( c ) , j ( у ) У j ( у ) , t = ^cJ ( c ) , t ,^{1 ( c} ) <  ^{j ( c} ) <  J ^{( c} ) ;

j ( у ) = ¹ ( у )

В том случае если c^ct - c^> 0, то точка, определяющая состояние иерархической системы управления, находится над плоскостью J(c) гиперплоскостей; если c^c^ t - c^с^ < 0 , то под плоскостью, а если c^c- c^с^ = 0, то принадлежит плоскости. Поэтому в нейронную сеть вводится преобразование вектора yt в вектор о = [^(с),..., ^(с),...,^J(c)J логических переменных следующим образом:

Xwhen c j ( c ) , t — c j ( c )> ^0;

^а j ( c )=i

^0 otherwise, где 0, 1 – логический ноль и единица соответственно.

Дизъюнктивные нормальные формы, построенные из элементов вектора а , позволяют разбить пространство у на Н областей Д,..., D ^ ,..., D _H , каждой из которых ставится в соответствие ^ -е значения векторов ^£ W ( t ) и ^£ w ( t ) , которые дают оптимальные настройки системы управления в этом конкретном режиме эксплуатации OUC. Дизъюнктивные нормальные формы имеют вид:

D = v

и

^{J ( c} )                /        \

1 < £ ,

c ft, c ) ^, j ( c > ( a i c ) )

Математика

J ^{( c} )

где D % — дизъюнктивная нормальная форма, описывающая область D % ; а Л^U, j ( c )⁽ ^ j ( c ) ) ^— и -я конституента единицы ^ -й нормальной формы; ^_OJ (_с)( ^ (_с)) — логическая функция переменной а^_с^ при ее вхождении в и -ю конституенту ^ -й нормальной формы.

Для нормальной работы нейронной сети на дизъюнктивные нормальные формы, описывающие области D % , накладывается ограничение:

D % n D z =0 , если % ^ Z .

Поэтому при принятии управленческого решения из всех областей, на которые разбивается пространство параметров, выбирается та единственная область D % , для которой D % = 1.

Настройка нейронной сети сводится к вариации параметров b      и c , определяющих расположение J(c) гиперплоскостей в пространстве параметров y, и выбору таких значений векторов W(t) и w(t), которые обеспечивают оптимальный режим функционирования OUC в этом состоянии.

Заключение

Таким образом, в результате исследования сформированы требования к структуре иерархической системы управления сложными многоконтурными объектами. Для контроллеров каждого уровня предложены типовые алгоритмы реализации их функций и определены характеристики контроллеров как физических приборов, выполняющих эти функции. Показано, что реализация оптимальных режимов эксплуатации объекта управления возможна за счет реализации на верхнем иерархическом уровне нейронной сети. Дальнейшие исследования в этой области должны быть направлены на представление контроллера с иерархической структурой как системы массового обслуживания, каждый элемент которой является одновременно и обслуживающим прибором, и генератором потока запросов на обслуживание, что позволит оптимизировать информационные потоки внутри системы иерархического цифрового управления сложным технологическим объектом.

Работа выполнена при поддержке гранта РНФ 24-29-20256.