Математическое обеспечение мониторинга состояния и управления режимами эксплуатации систем хранения криогенных продуктов

Вопросы обеспечения безопасности и снижения потерь являются доминирующими при хранении и транспортировке опасных веществ, находящихся в процессе стационарного хранения или перевозки в сжиженном состоянии. Разработка методов прогнозирования состояния продукта и способов сокращения потерь особенно актуальна для оборудования, в котором хранятся криогенные продукты (жидкий кислород, жидкий азот, сжиженный природный газ и др.). В последнее время отмечен устойчивый рост мирового рынка различных систем хранения криогенных продуктов (далее систем хранения), что обусловлено, главным образом, стабильным ростом производства и потребления сжиженного природного газа (СПГ). Для мирового рынка СПГ характерна устойчивая положительная динамика: в частности, рост по итогам 2021 года составил 5,4 %. При этом к 2035 году среднегодовой темп роста рассматриваемого рынка может возрасти вдвое [1].

Несмотря на наличие публикаций по теме бездренажного хранения криогенных продуктов, в том числе результатов компьютерного моделирования процессов тепломассообмена в различных криогенных сосудах, практически отсутствуют исследования по системному применению полученных результатов для снижения потерь при хранении и транспортировке криогенных продуктов в масштабах промышленного кластера и страны в целом [2]. При этом важнейшей составляющей системного подхода к предотвращению потерь при хранении и транспортировке криогенных продуктов является организация дистанционного мониторинга тепломассообменных процессов в стационарных и транспортных системах хранения, подключенных к единой информационной системе. Речь идет как о вновь проектируемых системах хранения, так и об оборудовании, находящемся в эксплуатации, которое следует обеспечить современными техническими средствами мониторинга и управления [3, 4].

Диспетчеризация и принятие решений при работе с криогенным оборудованием осложнено расположением систем хранения на удаленных друг от друга разнородных предприятиях, часть из которых принадлежит промышленному производству, а остальные относятся ко многим другим отраслям экономики. Например, большое количество систем хранения жидкого кислорода расположено на территориях металлургических предприятий, а также на объектах здравоохранения. При этом такие же кислородные системы хранения часто применяются на заводах, использующих газовую сварку или резку металла, на объектах стекольного производства, на предприятиях, изготавливающих световое оборудование и пр., технический кислород в сжиженном состоянии хранится и используется на предприятиях военно-промышленного комплекса и на объектах космической инфраструктуры [5]. Аналогичная ситуация с расположением систем хранения на разнородных предприятиях характерна для СПГ и других криопродуктов. Также особого внимания требуют вопросы управления режимами эксплуатации систем хранения, оборудованных холодильной машиной для реконденсации паров криопродуктов [6].

Расположение объектов мониторинга на сильно удаленных друг от друга разнородных предприятиях, учитывая, помимо прочего, различный уровень квалификации и опыта обслуживающего персонала, обусловливает необходимость разработки математического обеспечения и технических средств для повышения эффективности мониторинга и коррекции режимов эксплуатации систем хранения. Приоритетным направлением решения этой задачи в настоящее время является применение технологий искусственного интеллекта [7–9].

Функциональная схема рассматриваемой системы контроля режимов хранения криогенного продукта приведена на рис.

о к Сй

о

И О А ю о я я

E 1

Мониторинг окружающей среды

я я р о н я я о S

« к я к о н о о

Контроллер состояния

криопродукта

Рис. 1. Функциональная схема системы контроля состояния криопродукта

В состав системы входят собственно объект хранения и транспортировки, сенсорная подсистема, включающая датчики измерения состояния собственно объекта контроля (sensor) S 1 ,..., S k ,..., S K , датчики измерения параметров окружающей среды (environment) E 1 ,..., E j ,..., E J , средства воздействия на объект (drives) D 1 ,...,D m ,..., D M .

Объект контроля представляет систему сосудов, контролируемо сообщающихся между собой, а также с напорной и дренажной магистралью. Сосуды и магистрали снабжены контрольноизмерительными приборами и запорно-регулирующей арматурой. В состав датчиков измерения состояния S ₁, ..., S_k , ..., S_K собственно объекта контроля входят: датчики давления, температуры, уровней жидкой фазы внутри сосудов; концевые выключатели, идентифицирующие откры-тие/закрытие перепускных клапанов, а также клапанов, изолирующих сосуды от магистралей; датчики скоростей вращения валов, токи, напряжения, температуры электродвигателей приводов запорно-регулирующей аппаратуры, а также холодильной машины при ее наличии. При контроле параметров окружающей среды E ₁, ..., E_j , ..., E_J в системе используются датчики температуры, влажности, давления, концентрации газа в рабочей зоне. Если сосуд, заполненный криопродуктом, размещен на подвижном носителе, то в состав E ₁, ..., E_j , ..., E_J включаются датчики текущих линейных и угловых скоростей и ускорений носителя. Результат управления сводится к подаче управляющих воздействий D ₁, ..., D_m , ..., D_M на приводы перепускных, входных и выходных клапанов.

Большое количество контролируемых параметров от разных сосудов, высокие требования по безопасности и скорости реакции системы в целом на возникающие предаварийные ситуации предполагают интеллектуализацию процесса управления, например, за счет применения нейронной сети, обеспечивающей мониторинг состояния и установление режимов функционирования цифрового регулятора [10–12]. Структура нейронной сети приведена на рис. 2.

В нейронную сеть входят нейроны первого слоя V1 = (v1,1,..., v1a,..., v1, А), связанные с системой мониторинга, нейроны второго слоя v2 = (v i, —, v2 ^, —, v2 s), выходы которых подключены к входам логических блоков 21,...,Х^,..., 2 выбора режима функционирования системы хране- ния.

На вход нейронной сети поступает обобщенный вектор измеряемых параметров состояния X = ( Х^Х » ,—,Х а ) ,                          (1)

где Xa g(En...,Ej,...,Ej,S1,...,Sk,...,Sк); X„ = [x1(a),...,xpaa),...,x^)] - кортеж из последова тельно поступивших на обработку дискретных значений сигналов   E1, ..., Ej, ..., EJ,

S 1 ,..., S_k ,..., S K ; 1 <  а ; A = J + K .

Кортежи Xa представляются в пространственно-временных дискретных координатах, если сенсор формирует цифровой образ наблюдаемой сцены, или в дискретном времени, если сигнал формируется сенсорами другими типов. Номер элемента x    кортежа обозначен индекс функ цией в (а), где а - номер элемента Ха в векторе X. В случае линейной обработки, как это показано на рис. 2, выходные сигналы нейронной сети рассчитываются как свертка

В ( а )

x i ( а ) =   ^ ^а в ( а ) x i ( а ) -в ( а ) ^{,                                      (2)}

в ( а ) =1

где x^ g Х^ , 1 <  а < А , Х^ - последовательность отсчетов, формируемая на выходе нейрона; [ a i(«),..., ap(а),..., a^ («) ] — дискретный импульсный отклик фильтра, подбираемый при настройке сети; В ( а ) - размер апертуры фильтра, равный длине соответствующего кортежа и в общем случае неодинаковый для различных величин Х _а .

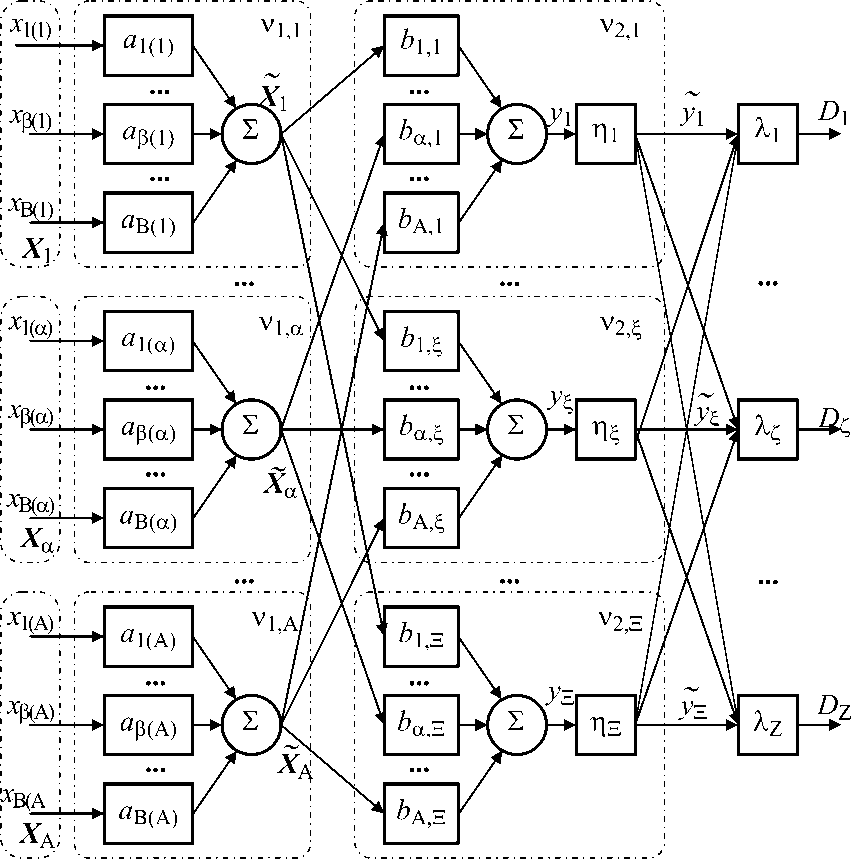
Рис. 2. Нейронная сеть мониторинга состояния и выбора режима хранения криогенных продуктов

Очевидно, что линейная фильтрация (2) не является единственно возможной для использования в нейронной сети. В ряде случаев, в частности в условиях импульсных помех в каналах передачи данных от сенсоров к сети мониторинга состояния и выбора режима хранения криогенных продуктов целесообразно применение фильтра, основанного на порядковых статистиках [13, 14]. В подобных фильтрах кортеж X _a , упорядоченный по последовательности поступления величин х(^ ,..., х ^^,..., х_в(^ на обработку, переупорядочивается по возрастанию указанных величин, т. е.

Xa ^ Xa,inc = ^x1(a,inc), xe(a,inc),xB(a,inc)] , где xe(a),inc G Xa , 1(a) ^ ^(«^ ^ B(a) i x1(a),inc ^ ™ ^ xe(a),inc " - " XB(a),inc •

Далее из кортежа Xa,inc выбирается элемент х^а^ с заданным номером. в(а,inc), который включается в кортеж Ха выходных величин слоя V1. В случае, если в (a, inc) = 1, то в процессе фильтрации выбирается наименьший элемент. В случае, если в (a, inc ) = B(a), то в процессе фильтрации всегда выбирается наибольший элемент. В случае если число B(a) является нечетным и при фильтрации выбирается элемент с номером e(a,inc)=[B(a)- 1]/2+1, то фильтр является медианным. При настройке нейронной В(а) и номер в(а,тс) выбираемого элемента.

На выходе подсети ν₁ первого слоя формируется вектор кортежей X = ( X 1 ,...,X _a , ...,Х _А ) в А -мерном пространстве оценок состояния системы хранения криогенных продуктов (рис. 3).

Привязка кортежей к единому дискретному времени, например к моменту в, позволяет сформировать вектор X (в) = [Х1 (в) ,-, Ха ( в),-.-, Ха( в) ,.•., ] текущих оценок состояния системы. Нейроны v2,1,..., v2,t,..., v2,H второго слоя формируют в рассматриваемом пространстве систему гиперплоскостей сети определяются размер апертуры

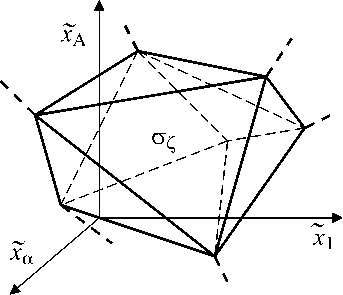
Рис. 3. Пространство оценок состояния системы хранения криогенных продуктов

b • x + c = 0,

~     ~       ~        ~  \ 0                                                                           ,           а где x = (Х1,...,ха,...,xА)  - координаты пространства оценок состояния; b - нхА матрица ко- эффициентов; c = (c1,..., Ct,..., сн ) - н-мерный вектор-столбец свободных членов; 0 - нулевой н- мерный вектор-столбец; 0 - знак транспонирования;

b =

b 1,1    .	..   Ь а ,1    .	..   b А,1
b 1, t   .	.. b at  .	.. b A, t
b 1,H   .	.. Ь ан  .	.. b А,Н

.

Подстановка в (3) вектора X ( в ) текущих оценок позволяет определить его местоположение у ( в ) в пространстве относительно сформированной системы гиперплоскостей:

b • x (e) + c = У (в),

где у ( в ) ⁼ [ У 1 ( в ) ,.•., Уе, ( в ) ,—, У _н ( в ) ] — вектор оценок местоположения вектора X ( в ) в пространстве оценок состояния.

Основной задачей нейронной сети является отнесение текущего состояния объекта контроля к одному из определенных классов и генерация последовательности действий в том случае, если класс, к которому отнесено состояние, не соответствует ожидаемому. Поэтому с помощью блоков П 1 ,—, П е , —, П н вектор координат у ( в ) преобразуется в вектор логических переменных у ( в ) = [ У 1 ( в ) ,..., y t ( в ) ,..., У н ( в ) ] ° следующим образом:

yt(в) =

1, when y t ( ^e ) >  0;

0 otherwise .

Физически логическая единица в (5) означает, что составляющая y t ( в ) вектора у ( в ) находится над плоскостью X = b 1 t X 1 ,..., b _a t X,..., b _A t а + C t = 0, а логический ноль - под ней.

Области а _х,..., a_z ,..., ^_z , в которые должен попадать вектор X ( в ) текущих оценок состояния, с использованием логических переменных y t ( в ) могут быть представлены в виде дизъюнктивных нормальных форм:

н

DZ = V Д ^z,t,i( yt)

, 1

i

где

^ SzЛ,i (y^ )

- i-я конституента единицы

Z-й нормальной формы; Sz Л i (У Л) —

логическая

функция переменной у^ при ее вхождении в i-ю конституенту, определяющую соответствую щую часть ^-й области.

Справедливо следующее утверждение.

Любая конституента задает выпуклый политоп в пространстве оценок состояния

Х1 ,..., Ха,..., ХА. Под выпуклостью политопа понимается то его свойство, что между любой парой точек, расположенных в его внутренней области, можно провести отрезок прямой без пересече ния с его внешними гранями.

Доказательство. Свойство достаточно просто доказывается методом математической индукции. Очевидно, что политопом, не имеющим внешних граней вообще, является неограниченное гиперпространство Х1,..., Ха,..., ХА, в котором между любыми двумя точками с координатами Х1 1,..., Ха 1,..., ХА 1 и Х1 2,..., Ха 2,..., ХА 2 может быть размещен отрезок прямой, не пересекающийся с гранями, которые в данном случае отсутствуют. Рассечем гиперпространство любой гиперплоскостью. Очевидно, что все отрезки, начинающиеся в точках, принадлежащих этой гипер- плоскости, и имеющие продолжение по одну или по другую сторону от нее, не имеют других точек пересечения с ней, если эти отрезки не лежат на самой гиперплоскости. Другие отрезки, начальные и конечные точки которых лежат по одну сторону от рассекающей гиперплоскости, также ее не пересекают. Поэтому в этом случае обе части гиперпространства, которые могут рассматриваться как два непересекающихся политопа с единственной общей гранью, также являют- ся выпуклыми.

Предположим, что после рассечения (к-1)-й гиперплоскостью гиперпространство Х1,..., Ха,..., ХА представляет собой объединение непересекающихся выпуклых политопов. Рассечем это пространство к-й гиперплоскостью и предположим, что сформированный предыдущими рассечениями l (к -1) -й выпуклый политоп рассекается на

l (к -1)   -й и

l (к -1)+

-й полито-

пы. Очевидно, что все отрезки, начинающиеся в точках, лежащих внутри l (к -1) -го политопа и оканчивающиеся внутри l (к -1)

—

-го политопа, не имеют других точек пересечения с к-й ги-

перплоскостью, кроме начальной, если эти отрезки не лежат на самой гиперплоскости. Другие отрезки, начальные и конечные точки которых лежат по одну сторону от рассекающей гиперплоскости, также ее не пересекают. Аналогичные рассуждения могут быть проведены и для l (к -1)+ -го политопа.

Таким образом, для базы индукции утверждение выполняется, и из предположения, что оно выполняется для (к-1)-го шага индукции, доказано, что оно выполняется на к-м шаге тоже. С учетом того, что l (к -1) -й политоп, сформированный на (к-1)-м шаге, был выбран произвольно, ут- верждение можно считать доказанным.

Отметим, что выпуклые политопы, описание которых представлено в виде конституент единицы, входящих в дизъюнктивные нормальные формы (6), покрывают все гиперпространство Х1,..., Х_а,..., Х_А. В общем случае каждая дизъюнктивная нормальная форма может описывать как выпуклый, так и невыпуклый многогранник о^,..., ^_z,..., <r_z, причем эти многогранники могут пересекаться между собой, если, например в групповые дизъюнкции входят одни и те же консти-туенты единицы.

Попадание вектора оценок X (в) в область а^, идентифицируемое по равенству единице Dz, означает запуск Z-го алгоритма коррекции состояния объекта, который может включать выполнение следующих действий:

• -    открытие/закрытие дренажных клапанов;

• -    открытие/закрытие перепускных клапанов;

• –    коррекция скорости и направления движения транспортного средства с цистерной;

• –    запуск/остановка двигателя холодильной машины;

• –    коррекция режима работы холодильной машины;

• –    продолжение мониторинга без выполнения действий.

Таким образом, использование предложенного математического обеспечения, реализованного на основе нейронной сети, повышает эффективность производственных процессов за счет автоматизации и интеллектуализации мониторинга состояния и управления режимами эксплуатации систем хранения криогенных продуктов. Предложенная схема потенциально эффективна для широкого спектра стационарных и транспортных систем хранения, в том числе оборудованных холодильной машиной для реконденсации паров криопродуктов.

Исследование выполнено при финансовой поддержке гранта правительства Тульской области в области науки и техники в 2023 г. (договор ДС/116 от 27.09.2023 г.)

• 1.    Исмагилова, В.С. Транспортировка трубопроводного и сжиженного природного газа: сравнительный анализ достоинств и недостатков / В.С. Исмагилова, Т.В. Чекушина // Науки о Земле и недропользование. – 2023. – Т. 46, № 1 (82). – С. 61–71.

• 2.    Солдатов, Е.С. Программное обеспечение моделирования и мониторинга процессов в резервуарах и цистернах при длительном хранении криогенных продуктов // Известия Тульского государственного университета. Технические науки. – 2019. – № 10. – С. 385–393.

• 3.    Larkin, E. Discrete Model of Mobile Robot Assemble Fault-Tolerance / E. Larkin, A. Bogomolov, A. Privalov // Lecture Notes in Computer Science. – 2019. – Vol. 11659 LNAI. – P. 204–215.

• 4.    Инерциально-спутниковая навигационная система управления транспортными средствами / В.Г. Макаренко, А.А. Подорожняк, С.В. Рудаков, А.В. Богомолов // Проблемы управления. – 2007. – Вып. 1. – С. 64–71.

• 5.    Архаров, И.А. О необходимости возрождения криогенного машиностроения в России / И.А. Архаров // Вестник Международной академии холода. – 2023. – № 1. – С. 6–9.

• 6.    Soldatov, E. Issues of Energy-Efficient Storage of Fuel in Multimodal Transport Units / E. Soldatov, A. Bogomolov // Smart Innovation, Systems and Technologies. – 2022. – Vol. 232. – P. 393– 402.

• 7.    Епихин, А.И. Мониторинг и прогнозирование расхода топлива судами с помощью нейронных сетей / А.И Епихин, М.И. Фадеев, И.Ю. Васаган // Эксплуатация морского транспорта. – 2023. – № 2 (107). – С. 104–107.

• 8.    Голосовский, М.С. Алгоритм настройки систем нечёткого логического вывода на основе статистических данных / М.С. Голосовский, А.В. Богомолов, Д.С. Тобин // Научно-техническая информация. Серия 2: Информационные процессы и системы. – 2023. – № 1. – С. 1–9.

• 9.    Nowak G. Using the Artificial Neural Network to Control the Steam Turbine Heating Process / G. Nowak, A. Rusin // Applied Thermal Engineering. – 2016. – Vol. 108. – P. 204–210.

• 10.    Digital Control of Continuous Production with Dry Friction at Actuators / E. Larkin, A. Bogomolov, T. Akimenko, A. Privalov // Smart Innovation, Systems and Technologies. – 2022. – Vol. 232. – P. 427–436.

• 11.    Large Scale Model Predictive Control with Neural Networks and Primal Active Sets / S.W. Chen, T. Wang, N. Atanasov et al. // Automatica. – 2022. – Vol. 135. – P. 109947.

• 12.    Технология построения инерциально-спутниковой навигационной системы управления транспортными средствами с нейросетевой оптимизацией состава вектора измерений / В.Г. Макаренко, А.В. Богомолов, С.В. Рудаков, А.А. Подорожняк // Мехатроника, автоматизация, управление. – 2007. – № 1. – С. 39–44.

• 13.    Sutton R.S. Reinforcement Learning, second edition: An Introduction / R.S. Sutton, A.G. Barto. – MIT Press, 2018. – 552 p.

• 14.    Application of Artificial Neural Networks in Condition Based Predictive Maintenance / J. Krenek, K. Kuca, P. Blazek, O. Krejcar, D. Jun // Recent Developments in Intelligent Information and Database Systems. Studies in Computational Intelligence book series (SCI, Vol. 642). – 2016. – P. 75–86.

Поступила в редакцию 13 января 2024 г.

MATHEMATICAL SUPPORT FOR MONITORING THE STATUS AND CONTROL OF OPERATING MODES OF CRYOGENIC STORAGE SYSTEMS

E.V. Larkin1, E.S. Soldatov2, A.V. Bogomolov3

• ¹    Tula State University, Tula, Russian Federation E-mail: elarkin@mail.ru

• ²    Research and Production Enterprise “Topaz”, Moscow, Russian Federation