Математическое обеспечение оценивания надёжности программных средств вычислительных кластеров

Интеллектуализация и цифровизация промышленных технологий предполагает существенное повышение производительности средств обработки данных [1–3]. Это может быть достигну-

Привалов А.Н., Богомолов А.В., Математическое обеспечение оценивания надёжности Ларкин Е.В., Акименко Т.А. программных средств вычислительных кластеров то за счет внедрения универсальных вычислительных кластеров, объединяющих множество независимых компьютеров-узлов в единую систему с общей файловой системой, высокоскоростной коммуникационной сетью и распределенной архитектурой [4, 5].

Широкое применение вычислительных кластеров актуализирует вопросы обеспечения надежности их аппаратных и программных средств. Надежность аппаратных средств обеспечивается за счет совершенствования технологий их проектирования, изготовления и эксплуатации, и в настоящее время является хорошо изученным вопросом [6, 7]. Программные средства вычислительных кластеров обладают рядом отличительных особенностей, выделяющих их среди других программных средств: параллельная обработка информации, высокая производительность, масштабируемость, повышенная отказоустойчивость, балансировка нагрузки, поддержка гетерогенных конфигураций - поэтому вопросы обеспечения их надежности требуют изучения [8-11].

Разработка технологий повышения надежности программных средств требует наличия модели формирования, выявления и рискометрии ошибок [12]. Структура модели должна формироваться по результатам анализа алгоритма функционирования вычислительного кластера, но не должна быть идентичной ему, поскольку ошибки программирования означают, что разработанное программное средство не соответствует заданным техническим требованиям, а модель должна выявлять именно эти различия, приводящие к отказам [13-15].

Основным недостатком известных подходов к оцениванию надежности программных средств [16, 17] является то, что:

• -    они ориентированы на исследование надежности программных средств однопроцессорных ЭВМ;

• -    оценки параметров надежности рассчитываются на основе эмпирических данных о количестве ошибок, выявленных между двумя наблюдениями за работой тестируемой программы, а следовательно, на результат оценивания сильно влияют как период наблюдения, так и покрытие области пространства обрабатываемых данных подобластью данных, генерируемых тестирующей программой.

Вместе с тем цена ошибки при анализе надежности вычислительных кластеров является, как правило, высокой, поэтому задача разработки надежной программы сводится к выявлению и устранению потенциальных причин отказов на этапе разработки, до ввода программных средств в эксплуатацию. Априорное оценивание надежности программных средств вычислительных кластеров на этапе их разработки недостаточно распространено в инженерной практике. Поэтому проведено исследование, имевшее целью разработку математического обеспечения априорного оценивания надёжности программных средств вычислительных кластеров.

Схема вычислительного процесса

Программные средства вычислительных кластеров в процессе разработки проходят следующие этапы [18], на каждом из которых возможно появление ошибок, обусловленных человеческим фактором.

Этап 1 . Разработка алгоритма, описывающего последовательную обработку данных в виде графа (рис. 1, а ), структура которого описывается выражением G = { A, r } , где A = { а о , a ₁,..., a j ,..., a j _{+ 1}} - множество вершин, каждая из которых является абстрактным аналогом оператора алгоритма; r = ^ r i , j ^ - матрица смежности размерности ( J + 2)( J + 2), описывающая связи между операторами алгоритма; r i , j- = ( a i , a j ).

В общем случае алгоритм включает неисполнимые операторы «Начало» ( a о ) и «Конец» ( a J _{+ 1}), а также J исполнимых операторов, представляемых вершинами a 1 ... a J . Оператор «Начало» выполняет перезапуск алгоритма, а оператор «Конец» моделирует завершение обработки данных. Факт перезапуска алгоритма моделируется с помощью дуги ( a J _{+ 1}, a ₀), показанной на рис. 1, а пунктирной стрелкой. В матрице смежности элемент r i,j = ( a i , a j ) обозначает дугу, ведущую из a i в a j ; 1 <  i , j <  J + 1. Значение r i , j = 0 , где 0 - пустой элемент, означает, что в структуре графа G дуга ( a i , a j ) отсутствует.

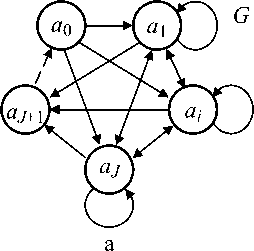
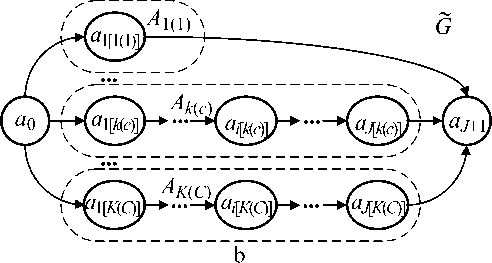
Рис. 1. Исходный последовательный алгоритм обработки данных в вычислительном кластере (a) и его линеаризованная версия (b)

Корректно сконструированный последовательный алгоритм обладает свойствами:

• -    в оператор «Начало» можно войти только при запуске программы, то есть r i , ₀ =0 ,0 <  i <  J + 1;

• -    попадание в оператор «Конец» означает остановку исполнения программы то есть r j +1, j =0 ,0 <  j <  J + 1;

• -    среди исполнимых операторов отсутствуют операторы, образующие автономные и полуав-тономные циклы первого и второго рода, то есть в структуре графа G существует хотя бы один путь, ведущий из а ₀ в a i , и хотя бы один путь, ведущий из a i в a J _{+ 1}, 0 <  i <  J ;

• -    каждый путь, ведущий из а₀ в a_J+ j, включает хотя бы одну вершину подмножества

^{{ a} 1 ,..., a j }.

Невыполнение любого из этих свойств означает, что при составлении последовательного алгоритма допущена ошибка, которая является источником потенциальных отказов программных средств вычислительного кластера.

Этап 2 . Линеаризация графа G, для чего матрица его смежности r возводится в с -ю конкате-национную степень, при этом формируется граф реализаций (рис. 1, б )

G = 1 ₀&

с (&)

c (&)=1

& I J +1 ,

где r ^{c (&)} - операция возведения матрицы смежности в c (&) -ю конкатенационную степень; & -обозначение логической операции конкатенации; I _R0 = ( а ₀, 0 ,..., 0 ), I _{CJ + 1} = ( 0 ,..., 0 , a _{J + 1}) ⁰ -соответственно вектор-строка размерности 1 х ( J + 2) и вектор-столбец размерности ( J + 2) х 1; 0 - обозначение операции транспонирования; C (&) - максимальное значение конкатенационной степени, в которую возводится матрица смежности r ; 0 - пустой элемент.

Возведение матрицы смежности в c( где & - матричная конкатенация; rc(&)—1 - [c(&) -1] -я конкатенационная степень матрицы r;

Конкатенация ранее построенной последовательности вершин с пустым элементом прерывает последовательность. Конкатенация IR 0 с матрицей смежности производится по правилам ум ножения вектора-строки на матрицу, а матрицы смежности с вектором IC J+1 - по правилам умножения матрицы на вектор-столбец.

В общем случае граф G имеет вид, показанный на рис. 1, б . Вершины графа образуют линей-

Привалов А.Н., Богомолов А.В., Математическое обеспечение оценивания надёжности Ларкин Е.В., Акименко Т.А. программных средств вычислительных кластеров ные (не содержащие циклов и ветвлений) последовательности A k ( c ) исполнимых операторов алгоритма, задействованных в k ( с )-й реализации. Последовательности имеют вид

Очевидно, что данные, обрабатываемые алгоритмом, являются дискретными и случайными.

Поэтому они могут быть представлены в виде множества векторов

Ц D m = { [ D 0 ( m )]..... [ D n ( m ) ].....[ D N ( m ) -1 ]Н ° «_И ’

—’D n ( Z ) >—>D N ( Z ) -1 } ’

m =1

где Dm = D^ ту—9 Dn(my.",DN(m)-i - множество дискретных значений обрабатываемой величины; D^  = [ D^  ..., Dn. ( m) >--->Dn ( M )] - обобщенный вектор обрабатываемых данных, описы вающий соответствующую комбинацию; n(Z) - номер комбинации; Ц - групповое декартово M произведение множеств; N (Z) = П N (m) • m=1

Фактор случайности значений дискретных данных, поступающих на обработку, описывается континуальной плотностью распределения, которая представляется в виде взвешенной суммы 8 -функций Дирака

N (Z)-1

f ( D ) =   Z   P n ( z ) К D — D n ( z ) ) ,

n (Z)=0(Z)

где pn(Z) - вероятность появления комбинации Dn(Z); S(D - Dn(Z)) - векторная 8-функция Ди рака:

К D — D n (Z) ) = К D 1 — D n (1) ) ■

K ( D m — D n ( m ) ) ■ ... K ( Dm - D n ( M ) ), J ... J ... j K ( D - D n (Z) ) d D = 1.

-да -x -x

Если элементы вектора D некоррелированы между собой, то для каждого элемента может быть определена плотность распределения

N ( m )-1

f m ( D m )

= Z p n ( m ) ^{К ( D}m ^{- D}n ( m ) ) *

n ( m )=0

А общая плотность распределения в этом случае равна произведению плотностей отдельных случайных величин, то есть

M f ( D ) =П fm (Dm ) *

m =1

Ветвление вычислительного процесса G определяется логическими условиями переключения из текущей вершины ai[к(c)] g Ак(c) в смежные с ней вершины из подмножества {ai}, 1 < i < J +1. В свою очередь, если ai[к(c)] = ai, где ai[к(c)] - вершина, принадлежащая последовательности, сформированной в результате конкатенации, а ai - вершина, принадлежащая под- множеству, то логические условия присоединения к последовательности Ак(c) вершины из под множества {ai} определяются вектором отношений ф=kj (D )< °] • где pi, j (D) - некоторая функция от данных дискретного пространства D , 1 < i < J +1.

Принимая во внимание, что в программе отсутствуют полуавтономные циклы, в том числе «зависания», одно из условий отношения вектора Ф всегда выполняется, события выполнения отношений являются несовместными и составляют полную группу. С использованием отношений вектора Ф может быть получена оценка вероятности того, что при следующем выборе ветви программы к последовательности A k ( c ) будет добавлена вершина a j , то есть a i [ _k ( _c ) _{] + 1} = a j будет равна

P{i[k ( c )] = i , i [ k ( c )] + 1 = j } = J ... J    ... J f ( D )d D .

P i , j ( D )<0

Вероятность появления последовательности A ^^ определяется как произведение вероятностей:

J [ k ( c )]

PA k ( c ) ] =     П     P { i [ k ( c )] = i , i [ k ( c )] + 1 = j} .

i [ k ( c )]=1[ k ( c )]

Преобразование G графа G является эквивалентным, поэтому можно считать, что ошибок на этом этапе не возникает. Однако такое преобразование позволяет выявлять следующие ошибки в исходном алгоритме:

• -    наличие в структуре G последовательностей с «неправильной» (большей или меньшей длины, определенной решаемой с помощью алгоритма задачи) длиной;

• -    выпадение из последовательностей структуры G операторов, необходимых для решения задачи;

• -    наличие в последовательностях структуры G «неправильных» и/или «лишних» операторов;

• -    наличие в последовательностях со структурой G фрагментов с неправильным чередованием операторов, например, нарушающим отношение предшествования.

Для указанных последовательностей могут быть определены вероятности их появления в структуре G , а также общая вероятность отказа/сбоя программных средств при реализации алгоритма со структурой G :

Pfail = Z P[k(c)] ’ k (c)

где k ( c ) - номера сбойных ветвей структуры G ; P [ k ( c )] - вероятности появления сбойных ветвей в структуре алгоритма, оцениваемые как вероятности появления последовательностей A _k ( _c ) .

Этап 3 . Формирование параллельной структуры из линеаризованной модели G .

Один из способов формирования параллельной структуры основан на разделении последовательности A _{k ( c} ) на L фрагментов, реализуемых на L вычислительных кластерах (рис. 2, а ).

Модель представляет собой сеть Петри

П = {{Пl}’ {ao, aJ+1}, {z0> zJ+1}, ^in {z0, zJ+1}, Tout {z0, zJ+1}} , где П l - подсеть, описывающая последовательность операторов, исполняемых l-м вычислительным кластером, 1 < l < L ; {a0, aJ+1} - позиции, моделирующие неисполнимые операторы алгоритма; z 0, zJ+1 - переходы, моделирующие соответственно начало и окончание параллельной обработки данных; Тin {z0, zJ+1 } , Т out {z0, zJ+1} - входная и выходная функция переходов; Тin(z0) = a0; Тout(zj+1) = aj+1; 4in(zj+1) = {Пt} ; ТoUt(z0) = {Пl}.

В свою очередь, подсети П l , описывающие вычислительные кластеры (в индексе функции l [ k ( c )] для краткости параметры k ( c ) опущены), имеют вид

Привалов А.Н., Богомолов А.В., Ларкин Е.В., Акименко Т.А.

Математическое обеспечение оценивания надёжности программных средств вычислительных кластеров

Пl   {{ai(k,l)} , {zi(k,l)},^in {zi(k,l)}, ^out {zi(k,l)}} , где   {ai(k,l)}   - множество позиций,   ai(k,l) g Ak(c);   {zi(k,l)}   - множество переходов;

*. [ z ( и ) ] = a i ( kJ ) ; * out [ z ,₍ kJ ) ] = a i ( JJ ) + 1, 1 ( k , l )< i ( k , 1 ) <  J ( ^k , l ) - 1.

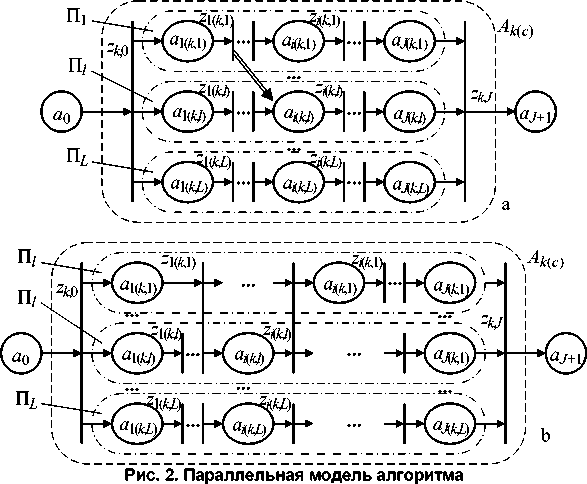
Сеть Петри описывает передачу управления от одного оператора к другому внутри вычислительных кластеров. Наряду с передачей управления внутри вычислительных кластеров естественным образом организуется передача данных, формируемых предшествующим оператором, всем последующим операторам. Простое разделение последовательности на фрагменты может породить ситуацию, когда данные, формируемые оператором m -го фрагмента, должны быть использованы операторами l -го фрагмента, а передача данных из m -го в l -й вычислительный кластер не предусмотрена (случай при m = 1 показан на рис. 2, а двойной стрелкой). Эта типичная ошибка распараллеливания может привести к отказу при реализации последовательности A k ( _c ) в целом, а следовательно, вероятность такого события входит в формулу для расчета p fail как одно из слагаемых.

Ошибки подобного типа устраняются программно за счет введения промежуточной синхронизации вычислительного процесса, проводимой на переходе z ₁₍- _k ,1) (рис. 2, b ). При промежуточной синхронизации

* in ^{[ z} 1( k ,1) ] = ^{{ a} 1( k ,1) , ^ai ( k , l )-1^} , * out ^{[ z} 1( k ,1) ] = ^{ a 2( k ,1) , a i ( k , l )^} .

Такое введение входной и выходной функции на переходе z^ _k ,1) замедляет процесс кластерной обработки данных, но уменьшает вероятность отказов программных средств.

Генерация потока отказов

Модель генерации потока отказов в вычислительном кластере приведена на рис. 3. Алгоритм генерации представлен в виде графа

Г = { A , р } , где A = { a ₀, a ₁, a ₂} - множество вершин; а ₀ - моделирует неисполнимый оператор «Начало»; а 1 - моделирует исполнимый оператор обработки данных в вычислительном кластере; а ₂ - моделирует неисполнимый оператор «Конец»; р = [ p i, j ] - матрица смежности размерности 3*3:

p =

^p i,2 0

0  ( a ₀, a 1 )     0

0   ( a i , a i )  ( a i , a 2 )

00  0

^p 0,1

P 1,1 0

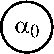
T e

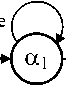
1 - p fail p fail ^\ ^a2 T exel

Рис. 3. Модель генерации потока отказов вычислительного кластера

При исполнении алгоритма в вычислительном кластере отказ происходит с вероятностью p fail и обработка данных прекращается. С вероятностью (1– p fail ) программа завершается и перезапускается в штатном режиме. Исполнение оператора а 1 осуществляется за время, равное T exe секунд.

Применение к матрице смежности p графа G , в котором 1 ₀ = ( a ₀, 0 , 0 ), 1 ₂ = ( 0 , 0,а₂)³ дает последовательности исполнимых операторов, сведенные в таблицу.

Формирование последовательностей исполнимых операторов

с	Последовательности операторов	Вероятность появления	Время до отказа
1	–	–	–
2	a 0, a 1, a 2	p fail	T exe
3	a 0, a 1, a 1, a 2	2 p fail	2T exe
k	a 0, a 1,..., a 1,..., a 1,... a 2 1       c - 1       1	P fi1	( c - l^T exe
K	a 0, a 1,..., a 1,..., a 1,... a 2 1      C - 1     1	Pfail	( C — I T exe

Из таблицы следует, что поток отказов может рассматриваться как стохастическая сумма потоков, формируемых при одно-, двух-, трех- и более кратном циклическом запуске вычислительного кластера. В соответствии с теоремой Б.И. Григелиониса, такой поток стремится к пуассоновскому [19]. Плотность распределения времени между отказами в пуассоновском потоке равна [20–22]

fff(1) = T-fe-tT-f, где Tbf – время наработки программного средства на отказ, оценка которого в предельном случае при С^х рассчитывается по зависимости

T bf = T exe p fail^.

Отметим, что при эксплуатации программных средств вычислительных кластеров ошибки, приводящие к отказам, как правило, устраняются [23–25]. Это означает, что количество сбойных ветвей в графе G уменьшается, а, следовательно, и уменьшается вероятность p _fail – время наработки системы до отказа при этом увеличивается.

Заключение

Таким образом, разработано математическое обеспечение оценивания надежности программных средств вычислительных кластеров, основанное на линеаризации исходного последовательного алгоритма и преобразовании его из линейной формы в параллельную. Поиск и оценивание вероятностей появления на линейной и параллельной форме ветвей, не удовлетворяющих требованиям технического задания на программное средство, позволило построить модель генератора отказов программных средств и обеспечить априорное оценивание времени наработки до

Привалов А.Н., Богомолов А.В., Математическое обеспечение оценивания надёжности Ларкин Е.В., Акименко Т.А. программных средств вычислительных кластеров отказа. Дальнейшее развитие исследований связывается с разработкой моделей отказов программных средств вычислительных кластеров вследствие структурных ошибок, допущенных при разработке параллельных программ.

Работа выполнена при поддержке гранта РНФ 25-29-20177.