Математическое обоснование эффективности использования методики малоинвазивного остеосинтеза закрытых переломов пяточной кости винтами

В настоящее время методом выбора при оперативном лечении переломов пяточной кости является открытая репозиция, остеосинтез пластиной [1, 4]. Применение этой методики имеет ограничения у больных с сопутствующей патологией (например, сахарный диабет) и часто осложняется некрозом ран, что обусловлено особенностью хирургического доступа [5].

На базе ГКБ № 1 им. Н.И. Пирогова нами успешно применяется малоинвазивный способ остеосинтеза закрытых оскольчатых «языкообразных» переломов пяточной кости тремя винтами.

Данный способ включает репозицию фрагментов перелома с помощью винта Шанца [3] под контролем электроннооптического преобразователя, введение спиц Киршнера через пяточную кость в тело таранной кости для временной фиксации отломков и остеосинтез 3-мя канюлированными винтами диаметром 4,0 мм по направляющим спицам [2]. Технический результат, достигаемый при осуществлении данной методики операции, состоит в профилактике осложнений, обусловленных раскалыванием отломков пяточной кости, а также исключении давления шлица винта на мягкие ткани за счет малотравматичных приемов проведения элементов, обеспечивающих остеосинтез; в улучшении функциональных результатов лечения за счет сохранения размеров пяточной кости; повышении надежности фиксации отломков за счет выбора траекторий введения фиксирующих отломки элементов в условиях достигнутой надежной репозиции. Таким образом, повышается стабильность остеосинтеза без укорочения пяточной кости при отсутствии срезающей нагрузки винтов.

В данной статье мы хотим предложить математическое обоснование эффективности применения методики малоинвазивного остеосинтеза в лечении переломов пяточной кости.

В работе предложена система фиксации пяточной кости при помощи трех винтов. Для теоретического обоснования данной схемы воспользуемся расчетами, применяемыми в механике стержневых систем [2]. При таком подходе о степени подвижности жестких элементов (дисков) системы судят на основании кинематического анализа. Для этого необходимо прежде всего определить число степеней свободы системы.

Число степеней свободы (W) — это минимальное число независимых параметров, необходимых для определения положения всех точек системы. Такими параметрами могут быть перемещения отдельных точек, углы поворота элементов и др. Очевидно, что для неподвижных систем W ≤ 0, а для подвижных W ≥ 1.

Для точки на плоскости W = 2, и в качестве параметров можно выбрать ее декартовы координаты. Чтобы однозначно определить положение твердого тела (диска) на этой плоскости, нужно задать уже три параметра. Например — координаты фиксированной точки A этого диска — X _A, Y _A и угол наклона φ принадлежащего ему отрезка AB (рис. 1). Таким образом, для диска W = 3, а система N дисков на плоскости будет иметь 3N степеней свободы.

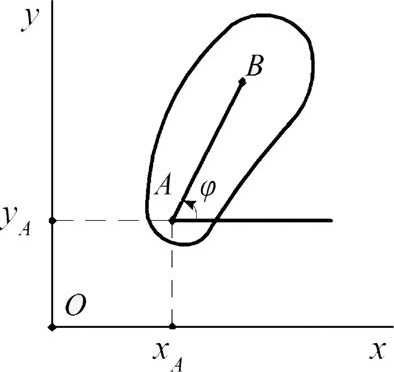
Рис. 1. Координаты, определяющие положение диска на плоскости

Для наглядности, мы ограничимся рассмотрением системы взаимосвязанных элементов отдельно по трем плоскостям осей координат. Неподвижность системы во всех трех плоскостях будет означать общую неизменяемость системы в простран- стве.

Рассмотрим систему, состоящую из двух дисков: D — обломок пяточной кости и D1 — часть пяточной кости, соединен- ная с таранной (рис. 2).

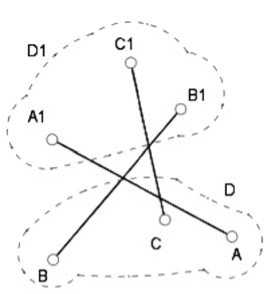
Рис. 2. Схематическое изображение соединения обломков кости

Число степеней свободы плоской стержневой системы определяется по формуле, называемой основной формулой кинематического анализа:

W = 3nд – 2nш – nc – nC0 – 3nп.

Здесь nд — число дисков; nш — число простых шарниров; nс — число стержней; nС0 — число опорных связей; nп — число припаек.

В нашем случае, число дисков равно 2, а значит система изначально имеет 6 степеней и опорных связей система не

свободы. Простых шарниров имеет, их можно исключить из уравнения. Жесткое соединение пяточной кости и таранной позволяет позволяет рассматривать его как припайку. Число стержней соответствует числу винтов (n), обеспечивающих связь.

Таким образом, число степеней свободы представленной системы двух дисков (обломков кости) определяется уравнением:

W = 6 – n – 3, учитывая, что для неподвижных систем W ≤ 0: 6 – n – 3 ≤ 0.

Откуда получаем, что n ≥ 3. Это означает, что число винтов, необходимых для жесткой фиксации отломка кости, должно быть не меньше трех.

Строго говоря, условие W ≤ 0 является необходимым, но недостаточным условием геометрической неизменяемости системы. Недостаточность здесь обусловлена тем, что такой подход имеет сугубо количественный характер и не может учесть дефектов в расположении связей. Так, например, некоторые связи системы могут дублировать друг друга. В общем случае может наблюдаться дисбаланс в распределении связей: их избыток в одном месте оставляет свободу для перемещений дисков в другой части системы.

По этой причине после количественного анализа — нахождения минимального необходимого числа несущих винтов, необходимо провести структурный анализ системы. Этот этап даст ответ на вопрос о правильном расположении винтов в системе D–D1.

Прежде всего, оси винтов должны лежать в разных плоскостях. Это условие необходимо для того, чтобы их можно было спроецировать на все три координатные плоскости. Таким об- разом, при рассмотрении трех разных координатных плоскостей мы получим по три проекции на каждой из них (рис. 3). Как уже было отмечено ранее, неизменяемость системы в трех плоскостях говорит о неизменяемости системы в пространстве.

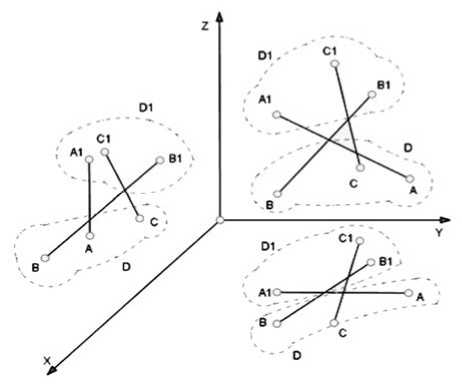
Рис. 3. Проекции винтовых соединений на координатные плоскости

Из этого условия следует, что оси винтов (равно, как и оси их проекций) не должны пересекаться в одной точке.

Для проведения структурного анализа рассмотрим проекцию двух дисков (D и D1) и соединяющих их винтов ( a, b, c ) на произвольно выбранную ось (рис. 1). Необходимость винта с доказывается геометрической изменяемостью системы из двух винтов.

Предположим, что два отломка пяточной кости соединены между собой двумя стержнями a и b (рис. 4).

В этом случае оси винтов неизбежно пересекутся в точке О. В случае двух параллельных винтов, считается, что точка пересечения О находится на бесконечном удалении от дисков. Между осями a и b образуется угол α. В терминах строитель- о 9

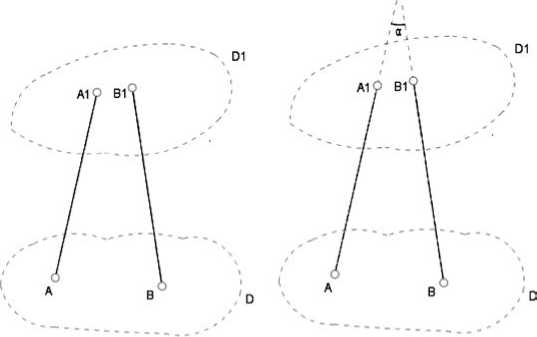
Рис. 4. Соединение отломков двумя винтами

ной механики, система, изображенная на рисунке 4, является мгновенно изменяемой. Действительно, зафиксируем винт a и попробуем увеличить угол α на бесконечно малую величину (рис. 5).

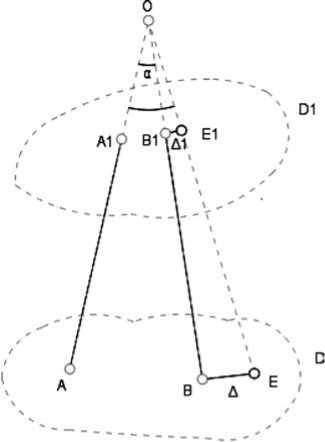
Точки соединения винта с костью B и B1 (точки приложения максимальной силы) преобразуются в таком случае в точки E и E1. Очевидно, что при фиксированном увеличении угла α, смещение Δ окажется большим, чем смещение Δ1. По этой причине в диске D возникают большие по величине напряжения, которые могут привести к разрушению кости. Даже бесконечно малое увеличение угла

Рис. 5. Вращение винта b вокруг точки О α приводит к заметному смещению точки B.

Именно для предотвращения этого, необходимо добавление третьего винта в систему.

При добавлении в рассмотренную систему винта с , его ось пересекается с осью винта b в точке O, образуя угол β (рис. 6).

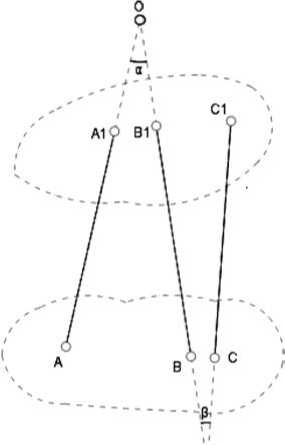
О О'

Рис. 6. Фиксация системы из двух винтов, введением третьего

В этом случае всякому изменению угла α соответствует противоположное по знаку изменение угла β. Это приводит систему двух дисков в состояние устойчивого равновесия.

Аналогично тремя винтами фиксируются отломки кости во всех трех координатных плоскостях: xy, xz и yz. Невозможность деформаций системы в этих проекциях говорит и о жесткости системы двух дисков в пространстве.

Таким образом, для эффективной фиксации двух костных фрагментов, необходимо и достаточно синтезировать их тремя винтами. При этом оси винтов долж- ны лежать в разных плоскостях и не пересекаться в одной точке.