Математическое обоснование предельного значения касательной силы тяги на ведущих колесах для транспортно-технологических машин

Целью данной работы является формирование математического аппарата для дальнейшего совершенствования математического моделирования движения колёсной транспортной машины с колесной формулой типа 4×2 с заднеприводной компоновкой. В статье рассмотрены факторы, влияющие на предельное значение тяговой силы на ведущих колёсах транспортной машины [1].

В качестве объекта исследования была выбрана унифицированная машина технологического электротранспорта, разработанная Ижевским государственным техническим университетом имени М.Т. Калашникова для Сарапульского электрогенераторного завода (СЭГЗ) [1, 2] в соответствии с постановлением Правительства Российской Федерации от 9 апреля 2010 г. № 218 «О мерах государственной поддержки развития кооперации российских образовательных организаций высшего образования, государственных научных учреждений и организаций, реализующих комплексные проекты по созданию высокотехнологичного производства».

Наземные транспортно-технологические машины при перемещении кроме перевозки грузов россыпью, навалом и т. п. могут выполнять различные технологические операции, например, различные виды работ (используются стандартные навесные устройства для различного передне- и задненавесного оборудования) при уборке снега, мелкого мусора, грязи и пыли [1–3], что требует анализа возможного максимального момента двигателя, подводимого к ведущим колесам и влияющего на эксплуатационные показатели, включая активную безопасность эксплуатации НТТМ.

Формирование математического аппарата

Математическим уравнением, которое определяет мгновенную возможность гарантированного движения, является уравнение силового баланса [3–5]. В общем виде уравнение силового баланса НТТМ можно представить в виде:

F_K =Σ Fc ,                                                                           (1)

где F_K – сила тяги на ведущих колесах, Н; Σ Fc – сумма сил сопротивления движению, Н, которая может быть представлена формулой [3]:

Σ Fc =   + Fw + Fa + Fj , где F^ – сила сопротивления качению автомобиля, Н; Fw – сила сопротивления воздуха, Н; Fa – сила сопротивления подъёму, Н; Fj – сила инерции, Н.

Дальнейшее усложнение не требуется, так как в данной статье силы сопротивления рассматриваются только как результирующий фактор, Σ Fc. При этом из уравнения (1) следует, что при FK>ΣFcпоявится ускорение ̈, равное, по второму закону Ньютона, ̈=       , где m – масса автомобиля.

Однако избыток силы тяги может вызвать отрицательный результат, например: пробуксовку колёс, продольное опрокидывание, выход из строя агрегатов трансмиссии из-за чрезмерной нагрузки [5–8].

Первые два фактора могут не позволить машине тронуться с места, как, например, при старте под углом на скользкой поверхности или при смещении центра тяжести к задней оси у переднеприводного транспортного средства. Также могут возникать ударные нагрузки в трансмиссии, которые приводят к увеличению вероятности выхода из строя агрегатов трансмиссии из-за чрезмерной нагрузки [7].

Поэтому при проектировании НТТМ необходимо найти баланс между избыточной и недостаточной силами тяги на ведущих колёсах. Рассмотрим НТТМ с колесной формулой типа 4×2.

Пробуксовка колёс – это наиболее часто встречающееся последствие избыточной силы тяги. Сила тяги при буксовании ведущих колес НТТМ

FtB =   ∙9∙соѕ(α) ∙λK∙φ, где m – масса автомобиля, кг; 9 – ускорение свободного падения, м/с2; φ – коэффициент сцепления колес с опорным покрытием, зависящий от типа и состояния покрытия, α – угол подъёма, град; λK – коэффициент нагрузки колес ведущей оси для НТТМ типа 4×2 в момент трогания, который определяется по уравнению [8]:

• 3   _ ^GD ± ^fa ,

λК=      , где Gd – масса, приходящаяся на ведущуюся ось колёс базовой НТТМ без навесного оборудования, Н; Fa – сила, действующая на ось от навесного оборудования, Н; G – масса НТТМ, Н.

Для ведущего моста с межколесным дифференциалом необходимо учитывать, что буксование будет возникать на колесе с минимальным сцеплением, следовательно, уравнение примет вид:

FtB = min(m∙9 ∙ соѕ(α) ∙ ^Ki ∙φi), где i – номер колеса ведущей оси (от 1 до 2); ^Ki – коэффициент нагрузки колеса ведущей оси.

Продольное опрокидывание практически не встречается сегодня на современных стандартных НТТМ. Но может возникнуть на грузовом и технологическом транспорте при нарушении условий эксплуатации, таких как превышение установленного веса транспортировки или погрузки. Кроме того, может даже привести к потере управления, в случае если вывешенная ось является управляемой, или даже к опрокидыванию при возникновении достаточного момента для смещения центра тяжести машины за ось [9].

Несмотря на то, что данная проблема почти не встречается на современных легковых серийных автомобилях, она крайне актуальна для технологического транспорта, в частности такого, который используется с навесным оборудованием.

В этом случае сила сопротивления опрокидыванию на ведущих колесах определяется по формуле

„ _ М_Ср

Ftp=, гк где тк – динамический радиус колеса, м; Meo – суммарный вращающий момент сопротивления опрокидыванию, который можно определить по формуле, Нм:

f^hl m ∙ 9 ∙ соѕ(α)        г ho m ∙ 9 ∙ соѕ (α)

Meo =    ⃗∙            dℎ+ ⃗∙            -dℎ, k0        dℎ                     ^ℎ, где для заднеприводной компоновки автомобиля: ℎQ – продольная координата центра задней оси, м; ℎ^ – расстояние от ℎQ до крайней точки транспортной машины по направлению действия силы тяги, м; ℎ – расстояние от ℎQ до крайней точки транспортной машины против направления действия силы тяги, м; ⃗ – радиус-вектор, направленный по направлению приложения касательной силы тяги.

Альтернативным, более простым для анализа выражением может быть суммирующая функция. Зная массово-габаритные характеристики агрегатов исследуемой НТТМ, можно рассчитать момент сопротивления из упрощенного уравнения как сумму моментов, создаваемых результирующим воздействием масс агрегатов по центрам их тяжести [10].

В этом случае формула для определения суммарного вращающего момента сопротивления опрокидывания:

Meo = ∑ i [ ⃗∙ m; ∙9 ∙ соѕ(α)] - ∑Ln[ ⃗∙ m; ∙9 ∙ соѕ(α)], где 1q – номер агрегата, центр масс которого расположен вертикально над осью; in , i_n– номера агрегатов, центр масс которых находится за пределами оси; m; – масса i-го агрегата, кг;

⃗ – радиус-вектор i -го агрегата, который находится из уравнения

⃗=ℎо -ℎa, где ℎ Ci – продольная координата центра тяжести агрегата.

На рисунке представлена поясняющая схема.

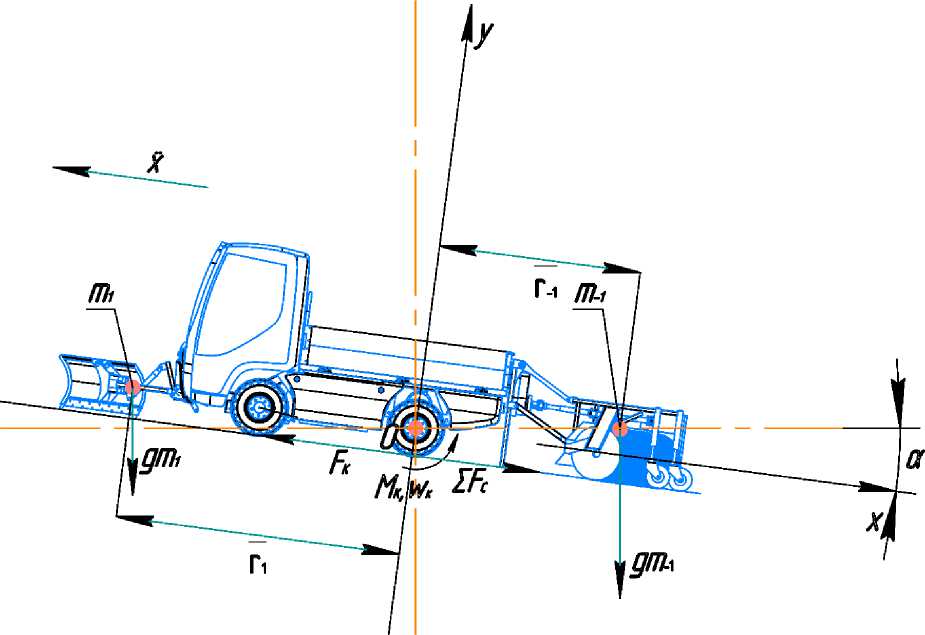
Схема приложения сил, возникающих при использовании навесного оборудования для расчёта опрокидывающего момента

Schematic of the forces arising from the use of attachments to calculate the tipping moment

На рисунке: , – эквивалент массы навесного оборудования в точке центра тяжести переднего плуга и задней щётки соответственно, кг; , – результирующая сила, Н; _, ⃗ – радиус-вектор, м; α – угол подъёма, град; O – координата центра вращения ведущей оси; x, y – относительные оси координат транспортного средства, MK – момент вращения на колесе, Нм; wK – направление вращения колеса; ̈ – ускорение транспортного средства, м/с²; F_K – сила тяги на колесе, Н; F_K – сила сопротивления движению, Н.

Разрушение элементов трансмиссии чаще всего происходит при нарушении требований эксплуатации, поскольку при проектировании закладывается нагрузочный режим с избыточной нагрузкой. Расчёты на предельную прочность трансмиссии проводят по трём режимам, а именно:

по максимальному моменту двигателя, по максимальным динамическим нагрузкам и по максимальному сцеплению ведущих колёс с дорогой [10–12].

Тогда для условия реализации максимального момента трансмиссией без повреждений сила тяги на ведущих колесах, приводящая к выводу из строя трансмиссии, равна [13]:

min ([ Mpt ])

FtM =            , где [Mpi] – предельный допустимый момент i-го элемента трансмиссии, Н·м.

Приведение к единой функции определения касательной силы тяги

Суммируя вышесказанное, можно сделать заключение, что при расчётах величина FK огра- ничена следующей системой неравенств:

(F_K >Σ Fc ;

j Fк < FtB ;

I ^Fk<  Ftp ; xF_K ^<  FtM ^.

Данная система при раскрытии рассматриваемых ограничений для максимальной касатель- ной силы тяги выглядит следующим образом:

^r                m ∙ g ∙ соѕ(α) ∙ A^i ∙φ ;

∑ io[ ⃗∙ mt ∙ g ∙соѕ(α)] -∑i-n[ ⃗∙ mt ∙ g ∙ соѕ(α)],

Fk <  min <

;

min ([ Мр^ ])

rK

Тогда предельно допустимая величина касательной тяги [ Fr ] будет равна

[ Fk ] =min( FtB , Ftp , FtM ).

F

Следовательно, при нахождении минимума данной функции будет определено предельное тяговое усилие на ведущих колесах, которое может быть реализовано на проектируемой НТТМ. Отметим, что при таких расчётах необходимо принимать коэффициенты сцепления шин с поверхностью дорожного покрытия φ как наиболее высокие [14].

Для практического применения расчёты более удобно производить от двигателя, причём, как правило, наиболее удобным является расчёт, исходя из создаваемого двигателем момента вращения [15–18].

Тогда с учётом передаточных чисел и КПД трансмиссии можно получить следующую зависимость предельно допустимого момента вращения двигателя [9] [ M_E ]:

^{[ F}A ]∙ ^K Ση∙Σ и ^,

[ M_E ]=[ F_E ]∙ r_E

где [Fe] – предельно допустимая тангенциальная сила на валу двигателя, Н; rE – радиус вала двигателя, м; Ση – суммарный КПД от вала двигателя до колеса; Σи – суммарное передаточное число от коленчатого вала двигателя до колеса.

Следовательно, предельно допустимый момент вращения двигателя равен

min	г                т ∙ д ∙ соѕ(α) ∙ Л^( ∙φ i ; ⎪ ∑ io[ ⃗∙Ш; ∙ g ∙ соѕ(α)] - ∑ i-n[ ⃗∙m; ∙ g ∙ соѕ(α)], ⎪
	TK                              ; ⎪                         min ([ Mpi ])                        ⎪
м       . ∙	⎩                            ^K                           ⎭
[]= [ мЕ ]=	Ση ∙ Σ и

Обсуждение

Выполненные исследования позволили построить формулу для расчета предельного значения касательной силы тяги на колёсах и формулу для определения предельно допустимого момента вращения двигателя на коленчатом валу двигателя, которые можно реализовать без буксования ведущих колес, опрокидывания и разрушения элементов трансмиссии, проектируемой НТТМ. Подобные работы актуальны и проводятся в странах с активно развивающейся автомобильной отраслью, а результаты таких работ публикуются в источниках высокого уровня [19–29].