Математическое описание процесса сушки зерна проса в аппарате с активным гидромеханическим режимом

Изучение аэродинамики движения и тепло-и массообмена частиц при сушке зерновых культур является важной составляющей при определении как режимов процесса, так и непосредственно геометрии сушильных аппаратов. В качестве объекта исследования нами было выбрано зерно проса, в следствии широкого распространения данной культуры на территории стран Евразийского экономического союза. Данная культура обладает высокими биологическими и химическими свойствами, но имеет низкую стойкость при хранении, чем обуславливаются повышенные требования при технологической переработке. В следствии этого нами был предложен ряд сушильных установок с активным гидродинамическим режимом и закрученными потоками теплоносителя с применением различных способов энергоподвода к продукту [1–2]. Для определения оптимальной конструкции установок необходимо производить инженерные расчеты, которые не могут быть адекватно рассмотрены без составления математических моделей.

Процесс СВЧ-сушки зерна проса во взвешенно-закрученном слое является чрезвычайно сложным с точки зрения физическо-математиче-ского описания. В основу модели данного процесса закладываются две составляющие: движение двух различных сред (газообразная среда – теплоноситель и сыпучая среда – зерно проса), взаимодействующих друг с другом и с рабочими поверхностями сушильной камеры, и тепло- и массообменные процессы в зернах проса. В данной статье нами подробно рассмотрена первая составляющая данной проблемы.

Во многих известных моделях аналогичных процессов сушки используют существенные упрощения (сферическая или цилиндрическая симметрия, сведение к процессам только в одном плоде) [3–7]. Однако, опираясь на возможности современной вычислительной техники, появляется возможность создать комплексную высокоадекватную модель процесса.

В настоящей работе поставлена задача определения основных уравнений, начальных и граничных условий математической модели процесса движения зерна проса во взвешенно-закрученном слое, обладающую высокой детализацией и высокой адекватностью, базирующейся на общепринятых методах моделирования и физико-математического описания, но использующей в полной мере вычислительные возможности современных компьютеров.

Для начала моделирования определяем количество одновременно находящихся в сушильной камере зерен проса, количество которых составляет порядка 104. Для моделирования механического поведения системы зерен проса, как сыпучей среды, используется метод динамики частиц, который в последние десятилетия широко используется в различных отраслях науки и техники. Метод заключается в решении уравнений движения множества отдельных сферически-сим-метричных частиц (зерен проса), которые испытывают силовое воздействие со стороны соседних частиц, потока теплоносителя, стенок сушильной камеры (рисунок 1).

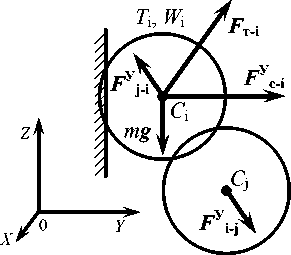
T ( x , у , z ), W ( x , у , z )

Рисунок 1. Силы, действующие на зерно проса в сушильной камере

Figure 1. The forces acting on the grain in a drying chamber millet

Уравнения движения зерен проса составляются на основе второго закона Ньютона:

<

d ² Xi   l (  (     AV

i me  dt2    T” vXm” X ‘, yi, zi     vxi

N с

V j = 1 j * i

d сП ("t

—

( Xj - X i - П )

ri - n )             ⁺ k n ⁽ r i - П

0, r - n z_

> d c -;

2 ^;

ri - П

dd

- у) ^Vxi , Г - n <  у^;

+

( Xi - Xi )

с ⁽ d e - r j )--------- ^{+ k}B ⁽ r j - d c ⁾⁽ V ,

d2 У.    /   (     (            .        , me W = km (( xi, У Zi)" ^‘

N с v j = 1 j * i

—

dc сП ( 2   r-П )

⁰ , r i - n -

> dc- ;

2 ^;

;

(yy^ + k n ( r - n

^r - П

d d

^- у) V yi , r i - n <  У;

+

⁽ ii - У])

^{e ( d}e - r j )------- ^{+ k}e ⁽ r j - ^dc ^{)( V}yi

—

;

d 2 z^

m e ^T = k m ⁽ ' ” ^{( X}i , У i , z i ) — vz i ) '

dc

⁽ z  z - П ) + kn ( Г--

ri - П

0, r - n z_

> d c ;

2 ^;

dd

^- у) ^vzi , r - n <  у;

+

N с v j = 1 j * i

( z i - z j )

с ⁽ d e - r j )--------- ^{+ k}B ⁽ r j - d c ^{)( V}z

—

^- m c g ,

где i – номер зерна; m с и d с – масса и диаметр i -го зерна; x i , y i , z i – декартовы координаты зерна; t – время; k т – коэффициент линейного вязкого трения при движении зерен в потоке теплоносителя;

v хт , v ут , v zт – компоненты вектора скорости телпо-носителя в месте нахождения i -го зерна; с и k в – коэффициенты жесткости и вязкости взаимодействия зерен с поверхностью сушильной камеры;

N с – количество зерен; j – номер зерна, возможно контактирующего с i -м зерном; с и k в – коэффициенты жесткости и вязкости взаимодействия зерен между собой; r i–П – расстояние от центра i -го зерна до поверхности сушильной камеры; x i–П , y i–П , z i–П – декартовы координаты точки касания зерна поверхности сушильной камеры; r ij – расстояние между центрами зерен i и j; v Хi , v уi , v zi – декартовы составляющие скорости i -го зерна; g – ускорение свободного падения.

Расстояние r ij между центрами семян рассчитывается на каждом шаге интегрирования через коор динаты центров по теореме Пифагора: r j = ( x ^- x j ) ² + ( У( ^- у / ) ² .

Уравнения (1) представляют собой дифференциальные уравнения второго порядка и решаются в процессе моделирования численным методом – методом Рунге-Кутта второго порядка:

x

= x " + V i • A t + а ^; • ( A t ) /2;

v ^{Т +1} = v ^r + ^; ■ А?; xi          xi        xi        ^;

у Г* = У Т + v ^T _yl -A t + a ; -( A t ) ² /2; v ;+ = ^ + а Т 'A t ;

z T ^{+ 1} = z ; + v ; -A t + a ; .(A t ) ²/2; v   = v ^T _zi + a ; -A t ,

Теплоноситель в рамках предлагаемой модели считается сплошной средой, сильно сжимаемой, и обладающей внутренней вязкостью. В этом случае, базовыми уравнениями, описывающим механическое поведение среды, являются уравнения Навье-Стокса, которые в трехмерном случае можно записать следующим образом:

d v d v     d v    d v        a dp

—x = - v —x - v —x - v —x + f+ dt      dx   y dy     dz

- f d2v   d2v    d2v )    f d2v   d2v   d2v)

+-- X + —- + —- + u\—x + — x + —у I;

p ^ dx2   dx dy  dx dz J    ( dx2   dy    dz2

X dvy     dvy = -vx —- - vy —- - v dx   y dy dvy z dz + Fy a p p dy +2p fd2 vx   d2 vy   d2 v' + —y + ^dxdy   dy    dydz) + Ц 'Sv, ldx d2 vy + —y + dy d 2 vy ' ^z" ) ;   (3) 5vz dt dv     dv = - v_ —z - v,. —z - v dx   y dy dv dz + Fz - a p p dz -+ p f d2 vx   d 2 vy   d2 vz —- + —- + —у v dxdz  dydz   dz2 + Ц '8X vdx d2 v +    + 8у 2 2vz^ ) dz2 J ; dp f dv,   d v,   dv, = - pl —x + —y + — ( dx   8y   dz )   dp I-vxlT" )    dx dp - v-- y dy dp vz ^’ dz _d t где i – номер семени проса, τ и τ+1 – индексы текущего и следующего временного шага; Δt – шаг интегрирования по времени; (xi, yi, zi), (vХi, vуi, vzi) и (aхi, aуi, azi) – положение, скорость, ускорение се-мени.vХ, vу, vz – компоненты вектора скорости среды в выбранной точке; t – время; Fх, Fу, Fz – компоненты вектора массовой плотности объемных сил, действующих на сплошную среду (сила в расчете на единицу массы); α – коэффициент пропорциональности плотности теплоносителя и давления (в приближении о линейной их связи); ρ – плотность теплоносителя в выбранной точке; λ – коэффициент сжимаемости среды; μ – коэффициент внутреннего трения.

Уравнения Навье-Стокса для сложных случаев не имеют аналитического решения, поэтому сразу будем ориентироваться на численное их решение с использованием метода дискретизации пространства и конечно-разностных схем [6]. Задачу будем решать в трехмерном пространстве XYZ . Для численного решения уравнений Навье-Стокса область моделирования, охватывающую сушильную камеру дискретизируем кубической сеткой. Область моделирования содержит 20 x 20 x 20 ячеек с размером ячейки d (рисунок 2).

В процессе численного решения уравнений Навье-Стокса на квадратной сетке необходимо для каждого узла ( i, j, k ) вычислять первые и вторые частные производные по каждой из координат x, y, z . Для расчета производных необходимо использовать значения функций v Х ( i, j, k ), v у ( i, j, k ), v z ( i, j, k ) и ρ( i, j, k ) в шестнадцати узлах, окружающих узел ( i, j, k ) (рисунок 3).

Не расписывая всю систему (1) в конечноразностной форме, покажем на отдельных примерах, как вычисляются первые и вторые производные:

dp ^ p^{; + 1} - p^; . d t       A t    ’

dp     ^p + 1,. j , k ^{- p} - - 1„ j,k .

dx ~      2 d’ d 2v     v ,, -, + 2v -, —v , -, vv         x,i+1, /,k           j,i, /,k        x,i-1, /,k x                  ,       , ,                        , , ,                   , ax2                 d2’

d vx     vx, i+1, j+1, k    vx, i+1, j-1, k    vx, i-1, j+1, k + vx, i-1, j-1, k дxdy4 где знак ≈ означает замену производной в уравнениях Навье-Стокса численной оценкой производной; τ и τ+1 – текущий и последующий шаги интегрирования по времени; Δt – величина шага интегрирования по времени; d – размер ячейки сетки дискретизации пространства.

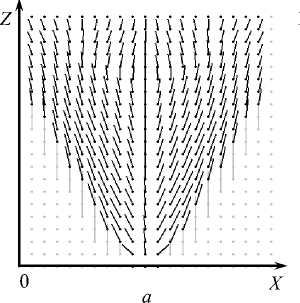
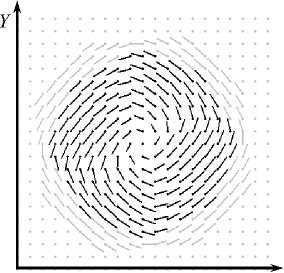
0                      X

б

Рисунок 2. Поля скоростей движения теплоносителя в сушильной камере в вертикальном осевом срезе (а) и в поперечном срезе на середине высоты камеры (б). Черными точками представлена внутренняя область сушильной камеры, серыми точками – область вне сушильной камеры

Figure 2. Movement velocity field of the coolant in the drying chamber in a vertical axial cut (a) and in cross-section in the middle chamber height (b). Black dots shown the inner region of the drying chamber, gray dots – the area outside of the drying chamber

сетке ( z ⁰ i = 0). Координаты x ⁰ i и y ⁰ i задаются случайным образом (с помощью генератора случайных чисел) в пределах круговой области удерживающей сетки. Начальные скорости механического движения элементов равны нулю:

v0= v0, = v = 0 .(8)

Начальная плотность воздушной среды во всех узлах равна равновесной плотности воздуха:

pjk = Po .(9)

Начальная скорость движения воздушной среды во всех узлах равна нулю:

v0    = v0   , = v0 , = 0.(10)

x , I , j , k      ^vi , I , j , k      ^vi , I , j , k

Граничные условия:

─ Механическое движение семян проса ограничено рабочими поверхностями сушильной камеры. Если в процессе движения семена внедряются в рабочую поверхность, в модели возникает возвращающая сила, пропорциональная величине внедрения, и под ее действием семена возвращаются внутрь сушильной камеры.

─ При решении задач тепло- и влагопере-носа граничными условиями считаются условия взаимодействия семян и окружающего их теплоносителя. В модели считается, что теплоноситель имеет постоянные в пространстве и во времени значения температуры TТ и влажности WТ.

─ Для уравнений движения сплошной среды граничные условия задаются в узлах, расположенных на границе сушильной камеры и теплоносителя.

Для определения этих узлов среди 20 x 20 x 20 узлов модельного пространства используются следующие неравенства:

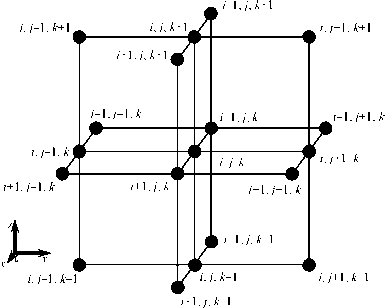
Рисунок 3. Индексация узлов, окружающих базовый узел (i, j, k), используемых для численного определения первых и вторых производных при сеточном решении уравнений Навье-Стокса

Figure 3. Indexing nodes surrounding the base node (i, j, k), used for the numerical determination of the first and second derivatives at the grid solution of the Navier-Stokes equations

Для определения начальных условий принимаем следующие допущения. В начальный момент времени семена проса располагаются в нижней части сушильной камеры, на удерживающей

4xtj. k ^{+ y} 2 j. k

R 1 ₊( R 2 - R 1 ) z i ^ j.! ^z

< d , ^V z , ,j k

^z i;

- |7 x^ jk + y , ² jk ^- R 21 <  d , при z _x <  z ,. j , k <  z 2 ;

| z,, j k — z2 I < d, при zij k > z2, где xi,j,k, yi,j,k, zi,j,k – координаты узла пространства (i, j, k); R1 и R2 – радиусы горловины и основной части сушильной камеры; z1 – высота перехода конической части сушильной камеры в цилиндрическую; z2 – высота сушильной камеры; d – размер ячейки пространства. В граничных узлах плотность среды считается равновесной ρi,j,k = ρ0, а скорость среды равна проекции на касательную плоскость к рабочей поверхности в данном граничном узле усредненного вектора скорости в соседних узлах (из внутренней области сушильной камеры).

Принимаем следующие допущения:

─ в пределах одного семени проса вещество считается сплошной средой;

─ теплоноситель является сплошной средой и подчиняется уравнениям Навье-Стокса;

─ механическое взаимодействие между семенами проса и с поверхностями сушильной камеры носит линейный вязкоупругий характер;

─ семена проса движутся по законам классической динамики, механически взаимодействуя между собой и с рабочими поверхностями сушильной камеры;

─ тепло- и влагоперенос между семенами проса и теплоносителем описывается соответствующими уравнениями в общепринятой форме;

─ температура и влажность теплоносителя постоянны в пространстве и во времени;