Материя и геометрия. ОТО и далее

Наиболее радикальные изменения в физике, порожденные сначала Специальной теорией относительности (СТО), а затем и Общей теорией относительности (ОТО) А. Эйнштейна [1], связаны с изменениями в фундаментальных представлениях о пространстве и времени. Одним из наиболее важных побудительных мотивов необходимости пересмотра представлений о свойствах пространства и времени в физике, начиная с конца XVIII века, являлось появление представления о физических полях. Хотя само понятие физического поля было введено Фарадеем в отношении магнитного и электрического полей в середине XIX века, но тесно связанное с ним понятие непрерывной среды, наделенной определенными физическими свойствами, появилось еще в работах математиков XVIII века, например, в работах Эйлера по гидродинамике [2] идеальной жидкости. В таком аспекте под полем вполне можно было понимать непрерывно распределенный в пространстве потенциал тяготения, появившийся в работах Пуассона [3].

С этой точки зрения сначала в физике существовало лишь одно физическое поле – поле тяготения. Проблема с понятием поля тяготения и необходимостью его введения состояла в том, что тела во Вселенной влияли друг на друга на больших расстояниях без видимой субстанции, которая могла бы служить причиной такого влияния. Однако никакие наблюдения пространства между телами не выявляли наличия какой-то заметной материальной структуры, переносившей взаимодействие

• ²Работа выполнена при поддержке Министерства Образования и Науки РФ (в рамках Государственного задания и проекта № 14.Z50.31.0015) и за счет средств субсидии, выделенной в рамках государственной поддержки Казанского (Приволжского) федерального университета в целях повышения его конкурентоспособности среди ведущих мировых научнообразовательных центров).

между Солнцем и планетами. Бытовавшее в XVIII и начале XIX веков представление об эфире в разных вариантах (светоносный эфир и тому подобное) не находили прямого подтверждения его наличия в природе. Его существование обосновывалось лишь невозможностью придумать что-то иное для объяснения наблюдаемых фактов влияния тел на расстоянии. Концепция дальнодействия представлялась большинству ученых еще более не ясной, чем представление об эфире. Понятие поля, предложенное Фарадеем, маскировало эту проблему введением формальных математических способов описания полей тяготения, магнетизма и электричества с помощью потенциалов и напряженностей. Слово “маскировало” означает, что материальная основа самого поля оставалась не совсем ясной, введение понятия поля было лишь удобной математической концепцией, позволявшей с успехом применять методы теории непрерывной среды.

В XIX веке ситуация усложнилась еще больше с появлением полевой теории электромагнетизма, предложенной Максвеллом. При этом проблема с физической интерпретацией электрического и магнитного полей нисколько не улучшилась по сравнению с полем тяготения. Заряды взаимодействуют на расстоянии между собой различными способами без всякой видимой субстанции, распределенной между ними, также как и в случае поля тяготения. В силу этого поиски такой субстанции стали еще более необходимыми. Существование некоторого влияния на пробные частицы (например, железные опилки) в пространстве между магнитами устанавливается простым экспериментом. Однако это, по сути, ничего не объясняет, а лишь констатирует факт наличия этого “нечто”, которое и получило название поля.

Однако математика XIX века совершила неожиданный переворот в понимании геометрии как таковой. В математике усилиями Гаусса, Лобачевского, Римана и Клиффорда, а также и рядом других математиков, появились пространства с геометрией, отличной от геометрии евклидова пространства. Сама геометрия оказалась способной наделять пространство множеством локальных свойств – кривизна, кручение, связность и так далее. Это открытие сразу было воспринято самими математиками как указание на то, что реальное, окружающее нас пространство также может быть наделено такими свойствами сложной геометрии. Например, Гаусс предпринимал попытки измерить наличие кривизны пространства с помощью измерения суммы углов треугольника, в вершинах которого располагались теодолиты, отдаленные друг от друга на километры. Хотя этот эксперимент не увенчался успехом, однако наличие такого нового математического инструмента позволило ввести в физику новые идеи, которые в дальнейшем позволили дать геометрическое толкование понятию поля. Однако прежде, чем это случилось в XIX после создания максвелловской теории, физика должна была решить другую, более практическую проблему.

Эта проблема была связана со свойствами инвариантности уравнений электромагнитного поля Максвелла. Как оказалось, уравнения этой теории инвариантны не относительно естественных для абсолютного пространства и времени преобразований Галилея, а инвариантны относительно преобразований Лоренца. Это означает, что уравнения Максвелла при переходе от одной инерциальной системы отсчета к другой по классическим законам должны изменять свою форму наподобие того, как меняют свою форму уравнения акустических волн в газовой (или упругой) среде. Фактически с классической точки зрения сама форма уравнений Максвелла подразумевает, что существует некая среда, в которой распространяются электромагнитные волны. Общепринятым названием такой среды в XIX веке был светоносный эфир. Проблема состояла в том, что в вакууме, не содержащем никаких материальных частиц, свет распространялся столь же хорошо, как и в воздухе. Таким образом, при интерпретации явлений электромагнетизма были возможны три основных концепции.

Первая состояла в предположении, что в вакууме все же есть нечто невесомое, называемое эфиром, структурные элементы которого настолько малы и специфичны, что мы их не можем обнаружить с помощью обычных экспериментов. Однако можно было предположить, что эти структурные элементы будут обнаружены в результате повышения точности экспериментов. Вторая интерпретация состояла в том, что пространство и время остаются почти такими же, как и в классической механике – атрибутами способа описания движения со стандартной евклидовой геометрией, но уже со специфическими свойствами, которые ему присущи по сути объединенного пространства-времени, которые ему позже приписал Минковский. Это означало, что само пустое пространство (без какой-либо среды) есть носитель специфической материи в виде электромагнитных волн. Такой подход собственно и был принят в СТО на основании экспериментов Майкельсона-Морли. Как показал эксперимент Майкельсона-Морли, материальной среды, такой как светоносный эфир, нет. Тогда приходится признать, что инвариантность уравнений Максвелла при переходе от одной инерциальной системы отсчета к другой являются фундаментальными. Но последнее возможно, если только меняются сами масштабы времени и координат при таких переходах. Поэтому преобразования Ло- ренца описывают свойства самого пространства-времени. С логической точки зрения эта интерпретация не объясняет саму природу электромагнитных волн и полей. В СТО не указывается – что же все-таки колеблется и переносится в пространстве в форме электромагнитных волн. Пространство-время Минковского не имеет подходящих атрибутов, которые могли бы быть связаны с волновыми степенями свободы электромагнитной волны. Пространство-время лишь объясняет сравнительные свойства материи в разных системах отсчета. Это приводит к некоторым парадоксальным следствиям, которые до сих пор вызывают дискуссии. Достаточно подробный анализ проблем СТО и ОТО был сделан еще Бриллюэном в работе [4].

Существовал и третий подход, который был сформулирован в общих чертах Клиффордом [7]. Он не относился только к электромагнитным волнам. Он вообще предлагал новый подход к объяснению свойств материи и ее динамики на основе введения более сложной геометрии самого пространства и времени. Клиффорд указывал, что, волны материи, в том числе и электромагнитные, могут быть проявлением свойств неевклидовой геометрии самого пространства наподобие волн на поверхности жидкости. Однако четкой математической теории, связывающей свойства геометрии и материи, предложено им не было. Вместе с тем такой подход можно рассматривать как наиболее приемлемый с логической точки зрения, поскольку геометрия может дать вполне ясное понимание того, что же все-таки колеблется и перемещается в пространстве, когда мы наблюдаем электромагнитные явления. В отличие от плоского пространства неевклидово пространство имеет целый набор функциональных параметров, которые можно связать со свойствами материи. Кроме этого, такой подход решает проблему наличия поля в “пустом” пространстве. Остается лишь решить проблему – какие физические характеристики материи и ее движения связаны с параметрами геометрии пространства? Первое решение этой проблемы было предложено Эйнштейном в рамках ОТО.

Решение проблемы объединения свойств материи и пространства-времени в ОТО отличается от подхода, предложенного Клиффордом. Идея Клиффорда состояла в том, что любое проявление материи есть проявление кривизны пространства (эта идея представлена в эпиграфе к данной работе). Решение Эйнштейна в ОТО состояло в том, что материя есть сущность отличная от сущности пространства-времени, но влияет на его геометрию. Геометрия же, в свою очередь, влияет на структуру и динамику материи. Подход Эйнштейна объяснил с помощью геометрии смысл поля тяготения, как проявления его кривизны. При этом, кривизну пространства можно обнаружить, исследуя динамику материи и изменения ее структуры. Однако электромагнитное поле таким образом объяснить не удалось, хотя по ряду внешних признаков эти поля очень схожи.

Одной из причин, по которой электромагнитная теория не вписывается в общую схему ОТО и требует привлекать электромагнетизм как особую материальную сущность, отличную по своей сути от искривления пространства-времени, является наличие двух типов зарядов, что нельзя простым образом в рамках римановой геометрии связать с какими-либо характеристиками римановой кривизны. На эту проблему можно взглянуть со следующей точки зрения. Пространство-время в ОТО не является собственно материальным объектом. Можно сказать так, что в пространство ОТО нельзя вбить гвоздь и тем самым отметить положение “материальной” точки пространства. Это, например, выражается в том, что расширение самого пространства в космологических моделях, то есть изменение его масштабного фактора, может происходить в ОТО с любой скоростью, превышающей скорость света, что запрещено, вообще говоря, для реальной материи. Такой сверхсветовой процесс расширения объявляется нефизическим, а его наблюдение ограничивается горизонтом событий.

1.    Обобщения ОТО

Для решения этой фундаментальной проблемы в XX веке были предложены несколько обобщений ОТО, которые старались решить проблему включения в теорию электромагнитного поля в такой же форме как и поле тяготения, то есть с помощью интерпретации электромагнетизма как проявлений геометрии пространства-времени, но, возможно, в более общей форме [6]. Попытки такого рода были предприняты самим Эйнштейном с помощью увеличения размерности пространства времени до пяти измерений и специфической редукции лагранжиана теории. Более развитая версия аналогичного подхода была предложена Калуцей [8] и Клейном [9] (теория Калуцы-Клейна). В этих теориях электромагнитное поле трактовалось как характеристика метрических свойств геометрии пятимерного пространства-времени и его связности, аналогичной по форме метрике и связности четырехмерного пространства-времени ОТО. Однако прямых подтверждений данные теории не получили при том, что они содержат ряд недостатков, которые не позволяют сделать эти теории достаточно подходящим претендентом на роль хорошей теории [10].

Кроме увеличения размерности пространства-времени для объяснения электромагнитных явлений с помощью геометрии предлагались и другие подходы. Они опирались на возможность изменять характер связности пространства-времени, не меняя метрических его свойств. Одной из замечательных теорий такого рода была теория Вейля [5]. В этой теории предполагалось, что при переходе от точки к точке пространства-времени, кроме требований на характер переноса параллельных векторов, что определяется выбранной связностью, необходимо еще фиксировать и изменение эталонов длины. Последнее требование выглядит логически безупречно. Однако данная теория оказывается также не лишена недостатков, и с точки зрения эксперимента выглядит избыточным требование изменения длины эталонов длины и времени в электромагнитных полях.

Другой способ модификации связностей пространства-времени по сравнению со стандартным подходом ОТО, который также призван объяснить электромагнетизм с помощью геометрии, был предложен Картаном [11] и состоял во введении в пространство-время кручения в форме антисимметричной части коэффициентов связности Кристоффеля. Такой подход также дает лишь частичное объяснение электромагнитным явлениям и приводит к ряду трудностей.

Кроме этих подходов существовали и другие модификации и обобщения ОТО, которые были призваны решить другие проблемы этой теории, например, теория Бранса-Дикке, явно уже не связанные с физической интерпретацией электромагнитного поля. В настоящее время существует много вариантов обобщений ОТО, которые комбинируют различные варианты предложенных подходов с увеличением размерности пространства-времени и введением различных типов связностей. Однако можно констатировать, что удовлетворительного геометрического объяснения электромагнитному полю в настоящее время нет при том, что сама ОТО содержит ряд очень существенных недостатков.

2.    Проблемы ОТО

На сегодняшний день СТО и ОТО рассматриваются как наиболее адекватные физические теории для описания явлений при скоростях, близких к скорости света (СТО) и вблизи тел с большой плотностью вещества (ОТО). Однако, как это было описано выше, по сути эти теории не отвечают на важные фундаментальные вопросы, ради которых и вводились радикальные изменения в физику в конце XIX – начале XX века. Как отмечалось, исчерпывающего объяснения электромагнитным полям ни СТО, ни ОТО не дают.

Одной из основных проблем ОТО, которые обычно считаются наиболее значимыми, является проблема энергии, состоящая в невозможности приписать гравитационному полю определенную энергию (см., например, [14, 15]). Эта проблема, в частности, не позволяет объединить ОТО с квантовой теорией, в которой основную роль играет оператор полной энергии. Однако существуют и другие важные проблемы, на которые не всегда физики-теоретики обращают внимание. Часть из этих проблем была сформулирована в работе Л. Бриллюэна [4]. Мы не будем воспроизводить анализ СТО и ОТО, проделанный Л. Бриллюэном в работе [4], а рассмотрим некоторые другие аспекты общей проблематики ОТО.

Одной из проблем, которые, как правило, не обсуждаются детально, является проблема выбора описания геометрии физического пространства-времени в форме общего 4-х мерного псевдо-риманова пространства с метрическим тензором g ij ( x ), i,j = 0,1, 2, 3, x = (x ⁰ , x ¹ , x ² , x ³ ). Основная идея такого выбора состоит в том, что все свойства материи и гравитационного поля могут быть описаны исключительно параметрами внутренней геометрии пространства-времени, без необходимости иметь представление о том, вложено ли это пространство-время в пространство большего числа измерений. Однако существуют некоторые формальные трудности при реализации такой идеи. Одна из таких трудностей состоит в том, что для нечетно-мерных пространств однозначное погружение в евклидово пространство на единицу большей размерности требует задания и метрики, индуцированной погружением, и гауссовой кривизны пространства. В то же время для четно-мерных многообразий сама гауссова кривизна выражается исключительно через метрический тензор [12](с. 288). Поэтому в трехмерном случае для понимания того, как выглядит физическое многообразие извне, недостаточно знать только риманову метрику. Надо знать еще и гауссову кривизну, которая является характеристикой внешней геометрии. Следовательно, если вложение реально существует, то при описании геометрии пространства-времени в ОТО мы упускаем какую-то важную информацию. Однако проблема на самом деле представляется гораздо более глубокой.

• 2.1.    Существует ли объемлющее пространство

С математической точки зрения проблема состоит в том, что, если объемлющее пространство существует, то описание геометрии с помощью метрического тензора может быть не только не достаточным, но и избыточным. Например, если в реальности трехмерное физическое пространство в момент времени t может быть вложено в евклидово пространство R4 размерности d = 4, то произвол в функциональной форме компонент метрического тензора резко сокращается и сводится знанию только одной функции высоты F(x1,x2,x3,t) и ее первых производных, вместо трех независимых компонент метрического тензора трехмерного риманова пространства (или шести пространства-времени). Под функцией высоты понимается функция, задающая трехмерную гиперповерхность в R4 с помощью уравнения: Х4 = F(x1, x2, Х3, t), где Х4 - выделенная некоторым образом декартова координата в R4. Действительно, если объемлющее пространство R4 существует, то метрический тензор на физической гиперповерхности в нем в момент времени t будет иметь следующий вид:

(2.1)

gae (x, t|F) = §ав + dxa дхв , a, в = 1 2, 3, в отличие от метрического тензора общего вида gae (x, t) с шестью независимыми компонентами, три из которых можно произвольно менять с помощью внутренних преобразований координат. Кажется, что общность метрического тензора риманова пространства включает в себя и вариант с погружением (вложением) в R4 , однако проблема состоит в том – можно ли уравнения динамики ОТО (уравнения Эйнштейна) простым образом редуцировать к уравнениям, допускающим решения в форме (2.1). Как известно, такая редукция возможна лишь в очень ограниченных случаях [13], поскольку редукция в такой метрике требует специфической формы тензора-энергии материи, которая реализуется только в очень простых физических полях. Отсюда следует, что, используя для описания геометрии пространства-времени общую метрику псевдориманова пространства, мы предполагаем, что вложение, если оно в реальности осуществляется в природе, соответствует размерности d = 7 объемлющего пространства. Последние числа взяты из известной теоремы о размерности евклидова пространства En , в которое может быть вложена гладкая риманова гиперповерхность размерности k. Согласно этой теореме вложение в общем случае возможно, если n = 2k + 1 (а погружение в пространство n = 2k). Таким образом, в ОТО существует неявный постулат, заставляющий предполагать, что наше физическое пространство может быть вложено в евклидово пространство размерности 7. При этом даже можно игнорировать проблему вложения псевдориманова пространства размерности 4 в псевдоевклидово пространство большей размерности, что само по себе представляет проблему для интерпретации.

В ОТО выбор метрики в форме общей римановой метрики поддерживается принципом общей ковариантности физических уравнений. Действительно, если этот принцип выполняется, то в любой системе отсчета физические уравнения выглядят одинаково. В то же время, если в реальности существует вложение физического пространства в евклидово пространство, то в природе будут существовать выделенные системы отсчета, связанные с равномерно движущимися системами отсчета в объемлющем евклидовом пространстве. Такое пространство можно отождествлять до определенной степени с абсолютным пространством классической механики.

Критический анализ принципа общей ковариантности ОТО проводился неоднократно. В частности, Фоком было предложено ввести в ОТО выделенные системы отсчета, связанные с гармоническими координатами [14]. Это решает, в том числе, и проблему энергии гравитационного поля. Дополнительный анализ принципа общей ковариантности можно найти в упомянутой работе Л. Бриллюэна [4], где указывалось на нереальность принципа общей ковариантности, например, исходя из простого требования существования при измерении адекватных задач часов и линеек, или других приборов. Нельзя связывать систему отсчета с телами, которые разлетаются вдребезги при соударении со стенкой. К этому общему анализу можно добавить, что одной из основных фактологических причин, по которой принцип общей ковариантности нельзя рассматривать как удовлетворительный, это наличие в реальном физическом мире инерциальных систем отсчета, связанных с удаленными звездами. Этот факт является очень веским аргументом существования евклидова или почти евклидова объемлющего пространства, с которым инерциальные системы отсчета могут быть связаны.

Кроме проблемы размерности и инерциальных систем отсчета существует еще и проблема, которую можно назвать проблемой протяженности. Проблема состоит в том, что имеет ли смысл наделять свойствами протяженности пространство-время в независимости от наличия в нем материальных тел. ОТО как раз предоставляет такую возможность. В частности, в случае отсутствия какой либо материи в пространстве времени оно может обладать определенной геометрической структурой, отличной даже от плоского пространства-времени Минковского. Однако в этом случае само понятие протяженности теряет всякий смысл, поскольку свойство протяженности связывается исключительно с материальными объектами и требует наличия эталонов длины и времени. В ОТО материя – принципиально иная сущность, чем материя в какой-либо форме. Следует отметить, что кривизна пространства также является свойством протяженности, но в каком-то объемлющем пространстве. Риманова скалярная кривизна рассчитывается из формальных характеристик метрических свойств пространства-времени, но по сути отражает тот же физический эффект, что и гауссова кривизна. Оба параметра кривизны могут быть выражены в терминах радиусов внешней кривизны. Следовательно, для измерения этой кривизны требуется наличие материальных линеек в объемлющем пространстве. Если объемлющее пространство существует, и само по себе наделено заранее такими свойствами, которые не требуют измерения ее кривизны, то физическая гиперповерхность позволяет ввести непротиворечивым способом понятие протяженности и собственной кривизны как характеристики этой протяженности.

• 2.2.    Заряд, масса и топология

Следующей общей проблемой описания материи в ОТО является проблема электрического заряда. Само понятие электрического заряда в ОТО не связано напрямую со свойствами геометрии пространства-времени, то есть не является каким-либо ее атрибутом, и связано со свойствами самой материи, которая описывается в ОТО независимо от геометрии. Поэтому на самом деле, проблема описания свойств электрического заряда относится не только к ОТО, но и к самой электродинамике, как классической, так и квантовой. Суть этой общей проблемы складывается из нескольких отдельных проблем. Первой проблемой является проблема дискретности электрического заряда. Второй проблемой является фактическая точечность электрического заряда электрона и, по всей видимости, и других элементарных частиц, что противоречит конечности их массы. Третьей проблемой является рациональное объяснение собственного магнитного момента электрона и других элементарных частиц. Кроме этих трех проблем, связанных непосредственно с понятием заряда имеются, как минимум, еще две проблемы, связанные с ним опосредованно. Это проблемы барионной асимметрии Вселенной и проблема нулевого суммарного заряда Вселенной.

Все эти три проблемы тесно связаны между собой и порождают другие проблемы, такие как проблемы перенормируемости моделей частиц в квантовой теории поля. Существенность этих проблем для понимания структуры частиц очевидна, но с момента открытия электрона задача решения этих проблем постоянно переносится на будущие теории. Даже современная хромодинамика не решает ни одной из них, относя эту задачу к будущей общей теории структуры элементарных частиц или теории Великого объединения.

Рассмотрим проблемы, связанные с электрическим зарядом, более подробно. Начнем с проблемы дискретности электрического заряда. В классической и квантовой электродинамике, как и в более общих вариантах квантовой теории поля, достаточно обоснованные объяснения для квантования электрического заряда найдены не были. Более того, вообще наличие в природе исключительно дискретных электрических зарядов ставит под сомнение фундамент даже классической электродинамики. В классической электродинамике в качестве исходного принципа предполагается существование пробных зарядов со сколь угодно малой его численной величиной. Последние необходимы для непротиворечивого введения понятия напряженности электрического поля. Напряженность электрического поля определяется как предел величины отношения силы, действующей на пробный заряд в данной точке пространства, к величине этого пробного заряда, когда последняя стремится к нулю. Предельный переход обеспечивает отсутствие искажений в распределении источников поля при внесении пробного заряда в область их содержащую. В противном случае классическое понятие напряженности перестает быть корректным. Пока физика работала с зарядами, значительно превосходящими заряд электрона, последний мог рассматриваться как элементарный пробный заряд. Однако, когда физика поставила своей задачей выяснение структуры элементарных частиц, в которой важнейшую роль играют именно заряды, кратные заряду электрона, но не превосходящие его значительно, а других пробных зарядов просто нет, то основания электродинамики как классической, так и квантовой, оказываются под вопросом. Фактически, на микроуровне строения элементарных частиц мы не имеем возможности пользоваться классическими понятиями напряжённости, потенциала и так далее. Последнее относится и к гравитационному полю, источником которого является масса.

Проблема с массой такая же, как и с электрическим зарядом. Поскольку строение материи определяется набором элементарных частиц с конечной массой покоя, которая ограничена снизу (частицы с нулевой массой покоя не в счет), то определение напряженности гравитационного поля также будет содержать неопределенность, связанную с отсутствием в природе пробных частиц достаточно малой массы. Пока речь идет о макромасштабах, то проблем нет. Но на уровне элементарных частиц проблемы неизбежно возникают.

Вторая из перечисленных проблем электрического заряда связана с тем, что, если частицы, в частности электрон, содержат в своей структуре точечный электрический заряд, то, согласно простым вычислениям, полная энергия такой частицы оказывается бесконечной. В силу связи E = mc ² бесконечной оказывается и масса таких частиц. Сама проблема состоит в том, что, с точки зрения эксперимента, электрон ведет себя как точечный объект, а с другой – обладает конечной массой. Конечности полной энергии электрона можно добиться, предполагая, что его заряд распределен непрерывно внутри некоторой конечной области пространства. Такая возможность существует и часто рассматривается как естественное предположение о структуре электрона. Подобная идея лежала, в частности, в основе доквантовой теории Ми [6] (c. 261–267), которая не оправдала в целом себя. Однако точечность электрона лежит в основе всей квантовой теории. Действительно, квантовый статистический постулат строится на том, что электрон – точечный объект, поскольку модуль квадрата волной функции ^( x , t) равен плотности вероятности p( x , t) = |^( x , t)|2 обнаружения электрона в заданной точке пространства с координатами x = (x, y, z) в момент времени t. Введение конечных по размерам областей, где сосредоточен заряд, требует сразу пересмотра всей квантовой теории с введением в нее явной нелокальности, что плохо согласуется со множеством других экспериментальных фактов. Кроме этого, введение области размазывания электрического заряда внутри конечной по размерам области пространства неизбежно ставит вопрос о том, что за специфическая субстанция наделена свойством создавать электрические поля, почему она распределена в конечных областях, хотя одноименные заряды отталкиваются и, наконец, почему всегда внутри частицы суммарная величина такого заряда равна строго дискретной величие – заряду электрона.

Можно даже полагать, что процедура перенормировок, успешно использованная в квантовой электродинамике для расчёта аномального магнитного момента электрона, порождена именно неточностью самого принципа введения напряженностей. Хотя теория перенормировок не отказывается от понятий электродинамики классической, но вводит некоторые виртуальные поля, порождаемые, с ее точки зрения, виртуальными частицами. Идеологическое несовершенство такого подхода отмечалась неоднократно, но другого успешного формализма для расчёта квантовых величин предложено не было, хотя теория перенормировок в рамках квантовой электродинамики, в частности, не позволяет решить вторую проблему заряда – конечность массы электрона и других частиц в более общих теориях. Все это подсказывает, что на уровне элементарных частиц должен действовать некий другой принцип введения электрического заряда, массы и полей с ними связанных, которые были бы лишены необходимости рассматривать бесконечно малые пробные заряды, а сразу объяснять их дискретность.

Кроме микроскопической неопределенности в понятии напряженности электрических полей и потенциалов, порождаемой дискретностью заряда, существуют и некоторые проблемы, связанные с глобальными свойствами Вселенной, которые также имеют отношение к понятию электрического заряда. Таких проблем, как минимум, две. Первая проблема носит название барионная асимметрия Вселенной , а вторую можно назвать проблемой нулевого заряда Вселенной . Проблема барионной асимметрии состоит в том, что современные теории частиц, в том числе квантовые, симметричны относительно перехода от элементарных частиц к их античастицам. Наиболее важным является то, что свойства частиц и античастиц оказываются абсолютно одинаковыми за исключением, конечно, самого заряда, которые противоположны у частицы и античастицы. Последнее означает, что в рамках современных общепризнанных теорий нет возможности понять то, почему наша Вселенная содержит в основе наблюдаемого вещества исключительно протоны, а не антипротоны. Попытки обнаружить в космосе островки (галактики или звезды) вещества, которое построено на основе антипротонов, не увенчались успехом. Предполагается, что процесс отбора между веществом и антивеществом произошел на ранних этапах развития Вселенной, но причин для такого отбора пока обнаружено не было. Поэтому такой отбор часто называют процессом спонтанного нарушения симметрии.

Вторая проблема состоит в том, что в настоящее время сумма всех зарядов во Вселенной равна нулю и была таковой и в прошлом. Наличие хотя бы одного избыточного заряда какого-либо знака должно было бы приводить к анизотропии Вселенной, которая не наблюдается в реальности. При

Рис. 1. Двумерный аналог ручки Уилера этом никаких специальных ограничений на величину суммарного заряда ни классическая физика, ни квантовая, ни СТО и ОТО не дают. Поэтому равенство нулю суммарного заряда является важным фактом, который можно рассматривать в качестве одного из фундаментальных свойств Вселенной.

Определенную подсказку в решении проблемы с дискретностью электрического заряда можно усмотреть в предложенной Уилером и Мизнером [31–33] топологической модели электрического заряда. Суть топологического подхода Уилера-Мизнера сводится к анализу распределения поля напряженности электрического поля в области пространства со сложной топологией типа “ручки”. Двумерный аналог такой структуры изображен на рисунке 1.

Как видно из рисунка 1, силовые линии электрического поля вблизи горловин ручки ведут себя как силовые линии области с противоположными зарядами. Из одной ручки линии выходят, а в другую входят. Фактически это означает, что область со сложной топологией типа ручки Уилера воспринимается внешним наблюдателем как совокупность двух заряженных объектов с противоположными по знаку, но равными по модулю зарядами. Поскольку внутри ручки силовые поля не имеют сингулярности, то энергия электрического поля такой структуры оказывается конечной. Таким образом, вводя области со сложной топологией можно получить частицы с зарядом и конечной энергией и, следовательно, массой. Однако такой подход имеет очевидные недостатки, которые отмечали сами авторы данной гипотезы. Это возникновение частиц только в форме пар противоположно заряженных областей и отсутствие естественного квантования заряда в такой модели. Эти два недостатка сводят на нет преимущества такой модели, но дают повод более внимательно и детально подойти к идее использования сложной топологии для объяснения свойств частиц с электрическими зарядами.

Следует отметить, что существовали и другие попытки построить геометрическую интерпретацию электрических зарядов. Примером может служить идея использовать в качестве моделей зарядов конические особенности риманова пространства-времени [18]. В этом подходе было показано, что конические особенности пространства времени ведут себя, как локализованные на космологической струне заряды. Появление нужного собственного поля взаимодействия струн с пробными зарядами определяется наличием чисто геометрической структуры пространства, как и в случае с ручками Уилера. Но, в отличие от подхода Уилера-Мизнера, конические особенности сами по себе являются негладкими структурами, причем эта особенность не точечная, а лежащая на одномерной кривой в пространстве. Это не позволяет интерпретировать такие объекты, как точечные заряды элементарных частиц. Существовали и более сложные модели, например, [34], которые также не дали ощутимых результатов.

Однако, поскольку сама идея использования топологии для построения полезной теории зарядов кажется очень привлекательной, то следует выяснить, что же представляется наиболее важным в идее Уилера-Мизнера. Анализ показывает, что наиболее ценным в таком подходе является представление, что электрический заряд является свойством глобальной структуры пространства, то есть ее топологии, и лишь формально связан с потоком некоторого поля через замкнутую поверхность. В результате использование идей дифференциальной топологии в теории структуры элементарных частиц предоставляет в распоряжение физики набор инструментов, связанных с возможностью ввести в теорию совокупность целочисленных топологических инвариантов, которые можно пытаться связать с зарядами и не только электрическими.

3.    Что может дать топология?

Идея введения зарядов элементарных частиц с помощью сложной неодносвязной топологии областей пространства, хотя и не позволяет адекватно что-то рассчитывать, тем не менее демонстрирует возможность опираться на топологические инварианты как на возможные элементы физических свойств материи. Последнее очень хорошо согласуется с идеями Клиффорда [7] о том, что материя – это проявление определенной геометрии пространства, и кроме этой геометрии больше ничего нет в физическом мире. Идеи Уилера-Мизнера лишь дополняют эту идею тем, что вводят в обиход физических теорий не только геометрию, но и топологию, которая во времена Клиффорда делала только первые шаги.

Что из себя представляют топологические инварианты? Это такие свойства объектов, например, областей физического пространства, которые не меняются при произвольных гладких их деформациях. Если такие инварианты оказываются связанными с физическими свойствами материи, то их можно будет назвать “инвариантами в квадрате”. Такие инварианты сохраняются не просто при изменении физических величин, а и при гладких деформациях самих физических систем, характеристиками которых они являются. Исходя из общих соображений, можно было бы ожидать, что в физике такие инварианты должны были бы давно идентифицированы. То, что это не сделано до сих пор по отношению к основным уравнениям, говорит лишь о том, что до сих пор рассматривались лишь тривиальные деформации систем, при которых топология не меняется.

Следует отметить, что топологические инварианты в действительности используются в квантовой теории [35, 36] и некоторых других разделах физики. В квантовой теории методы теории гомологий позволяют выяснять, например, свойства диаграмм Фейнмана в различных моделях реакций элементарных частиц [36]. Другой вариант использования топологических методов – это использование топологических инвариантов объектов в качестве модели зарядовых чисел. Такие модели называют топологическими зарядами. Последние, как правило, связаны с целочисленными величинами – степенями некоторых отображений. Важным при этом является то, что степени отображений и, как следствие, связанные с ними топологические инварианты, часто могут быть выражены через интегралы по соответствующим объектам. Примером может служить эйлерова характеристика многообразий. Для замкнутых ориентированных двумерных многообразий эта величина, в соответствии с теоремой Гаусса-Боне [16, 17], равна интегралу по многообразию от его гауссовой кривизны. Эта же величина может быть вычислена как степень отображения Эйлера поверхности в сферу или как индекс единичного векторного трансверсального поля на замкнутой поверхности [37, 38]. Поэтому топологические инварианты, типа эйлеровой характеристики, могут быть использованы в физике, как величины, аналогичные по своей природе дискретным зарядам или зарядовым числам лептонного заряда, барионного заряда и так далее.

Идея использования топологических инвариантов, как зарядовых чисел, привлекает внимание давно (например, [35, 36]). Такая идея кажется вполне приемлемой, поскольку сами зарядовые числа не имеют строгой интерпретации в терминах структуры частиц и отражают лишь некоторые свойства наблюдаемых их распадов. Что же касается использования топологических инвариантов в качестве электрического заряда, то эта идея выглядит очень привлекательной, но упирается в целый ряд проблем. Решение части этих проблем было предложено в работах [20–22, 24–28].

4.    Пространство и время

Предложенная в работах [20–22, 24–28] концепция тополого-геометрического описания электромагнитных полей с целочисленным зарядом строится изначально на предположении, что пространство и время находятся в таком же отношении к друг к другу, как и в классической механике. Концепция строится на предположении, что пространством, как таковым, является евклидово пространство размерности 4, в котором выделена физическая гиперповерхность V ³ размерности 3, геометрия и топология которой определяют все свойства материи. Время и “объемлющее пространство” при этом являются абсолютными. В связи с этим предполагается, что релятивистские эффекты, наблюдаемые при больших скоростях движения частиц материи в данной теории должны появиться не с помощью постулата конечности скорости света СТО, которое вводится “руками”, а в результате выяснения свойств частиц, которые появляются в данной концепции.

Разделение общего понятия пространства на две сущности, одно – собственно пространство-время R4 х R1 в классической форме и второе - гиперповерхности V3 “пространство-материя”, реализует идею Клиффорда о том, что свойства материи целиком определяются свойствами кривизны пространства, но пространства материального, а не формального! Смысл такой конструкции состоит в том, что свойство протяженности и кривизны может относиться лишь к материальным объектам. Внешнее пространство, в данном случае объемлющее пространство R4 , представляет лишь формальную модель относительной протяженности материальных объектов, то есть абсолютное пространство классической механики, но на единицу большей размерности. Свойствами же материи может быть наделена только материальная структура. Поэтому, когда предлагается использовать для объяснения свойств параметры геометрии, то с необходимостью следует признать, что такие параметры должны относиться к геометрии материального объекта, коим и является гиперповерхность V 3 . Использование для объяснений свойств материи именно параметров геометрии V 3 избавляет нас (по крайней мере, пока) не ставить вполне естественный для физики вопрос – из чего состоит эта гиперповерхность.

Геометрия некоторых материальных структур для построения квантовой теории поля и частиц с использованием ОТО широко применяется в теории струн и бран [19]. Трехмерное пространство – материя типа V ³ – в терминах таких теорий следовало бы называть 3-браной. В отличие от этих теорий предложенный подход опирается не на идеологию ОТО, а строится на основе специального описания геометрии пространства-материи (или 3-браны), с помощью которого вводится изначально постулат топологической интерпретации электрического заряда, как эйлеровой характеристики областей пространства-материи, выделенных специальным способом. В рамках такой идеологии показывается, что предлагаемая концепция удовлетворяет принципу соответствия классической физике и квантовой нерелятивистской механике, включая электромагнитное поле и поле тяготения Ньютона. Это дает основания считать, что концепция такого типа может служить подходящим основанием для создания общей теории элементарных частиц и полей.

Поскольку в качестве постулата предлагаемой теории используется представление пространства-материи как трехмерной гиперповерхности V ³ , вложенной в евклидово вещественное пространство R ⁴ , то его геометрия может быть описана полностью одной функций F ( x , t), называемой функцией высоты, которая задает V ³ в виде уравнения:

и = F ( x , t).

(4.1)

В этом уравнении x = (x, y,z) и и декартовы координаты в пространстве R 4 , а t - время. Для того, чтобы уравнение (4.4) имело смысл, необходимо иметь возможность выделять в каждый момент времени гиперплоскость P ³ с декартовыми координатами x и ортогональное к нему направление U ¹ с координатой и. В теории предполагается, что такое разделение R 4 = P ³ х U ¹ эффективно связывается с выбором инерциальной системы отсчета и определяет “среднее” положение V ³ в R ⁴ в каждый момент времени. В символической записи связь между гиперплоскостью P ³ е R4 и пространством-материей можно представить следующим образом:

< V ³ >= P 3,

(4.2)

где угловые скобки означают некоторое усреднение гиперповерхности V ³ по всем координатам P ³ . Такое усреднение может быть определено следующим образом. Пусть существует некоторая неотрицательная, инвариантная по отношению к преобразованию инерциальных систем отсчета, функция p( x ,t), c помощью которой можно ввести усреднение функций координат, заданных на P 3. Тогда в каждый момент времени t существует число:

Fo(t) = У

R ³

F( x , t)p( x , t)dV.

(4.3)

В этом случае положение гиперплоскости P ³ следует определить по аналогии с (4.1) с помощью соотношения:

и = Fo(t).

(4.4)

Поскольку усреднение должно проводиться по всему P ³ , то можно предполагать, что зависимость Fo(t) должна, вообще говоря, исчезать, что как раз и соответствует определению инерциальной системы отсчета. Однако, если усреднение проводится лишь по некоторой части P ‘ 3 е P 3, связанной с выбранным телом отсчета, то зависимость Fo(t) может не исчезать. Более того, при усреднении по P ^{′ 3} , представляющей лишь ограниченную область некоторой гиперплоскости P ³ , то уравнение гиперплоскости P ^{′ 3} по отношению к системе координат “инерциальной” гиперплоскости P ₀ ³ может иметь следующий вид:

и = Fo(t) + Q a (t)x ^a ,

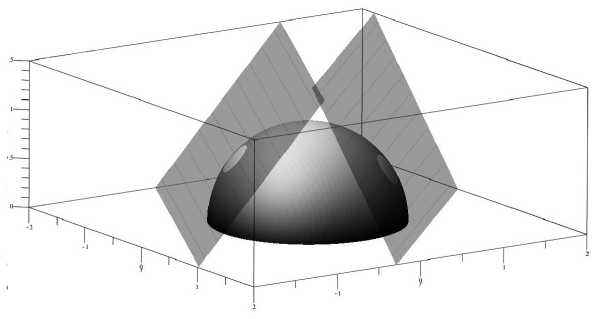
Рис. 2. Иллюстрация двух средних гиперплоскостей в точках, разнесенных на космологические расстояния

где Q _a (t) — однородное векторное поле на P03, задающее наклон гиперплоскости P ‘ ³ по отношению к P03. Преобразование функции F ( x , t) при переходе от P03 к P ‘ ³ при этом выглядит так:

F ‘ ( x ‘ , t) = F ( x , t) — F q (t) - Q a (t)x ^a .

Такие преобразования по сути генерируют силы инерции, поскольку градиент F будет восприниматься как добавочное поле сил в системах отсчета двух наблюдателей. Однако их роль может оказаться гораздо более серьезной на уровне космологических расстояний. Если пространство V ³ на космологических масштабах имеет некоторую среднюю кривизну с радиусом кривизны порядка космологических расстояний, то отличие средних гиперплоскостей P ^{′ 3} в разных точках Вселенной может порождать и красное смещение и восприниматься как ускоренное расширение (см. рис. 2). Это возможно по той простой причине, что средние гиперповерхности имеют некоторый угол наклона между собой в объемлющем пространстве, что воспринимается как отличие ускорений соответствующих систем отсчета. Такой подход может радикально изменить наши представления о процессах эволюции Вселенной.

5.    Электрический заряд как топологический инвариант

Главной проблемой, которую следует разрешить, используя топологическую интерпретацию заряда, является совмещение при описании электромагнитных полей частиц их точечности и конечности энергии. Необходимость такого совмещения, как уже отмечалось, диктуется тем, что, в частности, электрон ведет себя как точка, а с другой стороны, имеет конечную массу. В результате, необходимо иметь такое описание полей, при котором физические поля точечного объекта, сопоставляемого частице типа электрона, не имеют сингулярностей и непрерывны, но кулоновская особенность обязательно воспроизводится, как артефакт описания.

Идея такого подхода была предложена в работах [21, 22, 28]. Суть ее заключается в том, что с гладкой функцией высоты F гиперповерхности V ³ в R ⁴ связывается поле геометрических маркеров e ^a ( x , t), a = 1,2, 3. Зависимость e a = e ^a ( x , t) от x и t задается соотношениями:

F = F q + e 2| e | ² , | e | ² = ( e ¹ ) + ( e ² ) + ( e ³ ) ,                         (5.1)

которые должны выполняться на каждой отдельной области, содержащей экстремум функции F со значением F q. Здесь e = ±1. Знак e = — 1 соответствует максимуму, а e = +1 - минимуму. В этом случае в точке экстремума всюду гладкой функции F с координатами xq: d F /дх ^а | _х = _{Х о} = 0 выполнено условие: e a ( x Q ,t) = 0. Последнее условие указывает на то, что каждая изоповерхность функции F в области вблизи экстремума отображается в сферы радиуса R = 2|F( x ,t) — F q | в пространстве маркеров E ³ .

На пространстве маркеров E ³ теперь можно рассмотреть два дифференциальных тождества:

=^{4n5( e )}, ∂e ^a | e | ³

de a e a = ³'

(5.2)

Эти два тождества являются прообразами уравнений электромагнитного и гравитационного в классической физике. Действительно, если перейти в этих тождествах к координатам на гиперплоскости P ³ , получаем уравнения:

д                      d

(5.3)

_dx a D ^a = 4ne5( x ^a - x a ), _dx a G ^a = 4nG|J|.

Здесь введены обозначения:

D ^α

ε|J| ∂x ^α _{e a G α} | e ( x ,t)| ³ de a ,

₌ 4nG ^dx a

3 J ¹ de a '

В этих соотношения J = det вания e → x .

( de a /dx “ )

– определитель матрицы Якоби, координатного преобразо-

Нетрудно видеть, что соотношения (5.3) представляют собой классические уравнения для электрического поля индукции и поля тяготения, если поля D и G отождествить с полями электрической индукции и напряженности поля тяготения соответственно, а функцию |J | отождествить с плотностью массы: p = | J|. В работах [24-27] было показано, что соотношения (5.3) можно непрерывно продолжить на все пространство P ³ , дополняя их некоторыми граничными условиями для J . При этом первое уравнение (5.3) приобретает вид:

∂^∂x α ^{D α}

N

= 4п ^ Ek6(x“ - xa), k=1

(5.4)

где сумма берется по всем критическим точкам функции F , включая экстремумы и седловые точки. При этом второе уравнение для G остается неизменным. В результате полученные соотношения можно рассматривать как математическую модель совокупности целочисленных точечных заря- дов, знаки и величина которых определяются целыми числами εk , которые были введены формулами (5.1). Такие точечные заряды обладают некоторой массой, которую следует вычислять по формуле:

M = т ₀

|J|dV,

V

(5.5)

поскольку |J| отождествляется с плотностью массы. Область V , по которой берется интеграл, определяется теми условиями, которые определяют понятие частицы в такой модели.

В [24–27] показано, что наиболее адекватным способом определить частицу – это связать ее с областями P ³ (соответственно и V ³ ), которые ограничены особыми изоповерхностями функции F, на которых лежат седловые точки этой функции. Все конечные области пространства P ³ разбиваются на компактные области, ограниченные такими особыми изоповерхностями, что позволяет непротиворечиво ввести материальные структуры, связанные с “кривизной” V ³ . Топологическая структура V ³ может быть неодносвязной и содержать структуры типа ручек Уилера. Согласно [24–27], области пространства P ³ , внутри которых содержатся ручки Уилера V ³ , отождествляются с барионным зарядом, что позволяет включить в классификацию частиц не только лептоны, мезоны, но и барионы. Кроме этого, включение в теорию неодносвязных областей типа ручек Уилера однозначно обосновывает интерпретацию F как функцию высоты гиперповерхности V ³ , поскольку в неодносвязной области V ³ с координатами на P ³ функция F оказывается многозначной. Физическая полевая функция может быть многозначной лишь в случае, если каждому листу этой функции соответствует отдельный лист V ³ . Этот вывод опирается на постулат, что физический прибор в конкретной точке пространства может получить в качестве измерения только одно значение физической величины.

Наиболее важным обстоятельством, связанным с уравнениями (5.3) и (5.4), является то, что суммарный заряд, связанный с ними: Q = N =_{k = k} E k , как было показано в [24-27], равен топологическому инварианту – эйлеровой характеристике областей V на V ³ с границами ∂ V в виде особых изоповерхностей функции F:

N              1

Q = ^ek = x⁽V) = ^ x^(dV )•                            ⁽⁵-⁶⁾

k =1

В такой модели именно гладкая структура гиперповерхности V 3, связанная с F , порождает все необходимые для электродинамики величины – целочисленные точечные заряды, связанные именно с топологией этой гиперповерхности. При этом кулоновские особенности, присущие точечным зарядам, появляются в теории в качестве артефакта описания, использующего понятие геометрического маркера. Кроме этого, в теории сразу появляются и другие зарядовые числа, в частности, барионный заряд. Такое представление об электрическом заряде позволяет получить простую классификацию топологических структур областей пространства V 3 , которая имеет удивительное сходство с современной зарядовой классификацией элементарных частиц. На рисунке 2 изображены структуры простейших областей пространства V 3 с указанием эйлеровой характеристики границы области и соответствующего электрического заряда области. Эти простейшие структуры удивительно просто сопоставляются лептонам.

Рис. 3. Структура простейших областей V ³ , в сопоставлении с зарядами лептонов. Последняя структура – гипотетический лептон с зарядом 2

Следуя такой схеме, барионам следует сопоставить области пространства, имеющие границы такие же, как и на рисунке 3, но содержащие в своей внутренней структуре трехмерные ручки Уилера (см. рис. 1). Двумерный аналог таких структур представлен на рисунке 4, соответствующих протону и антипротону с указанием их барионных зарядов.

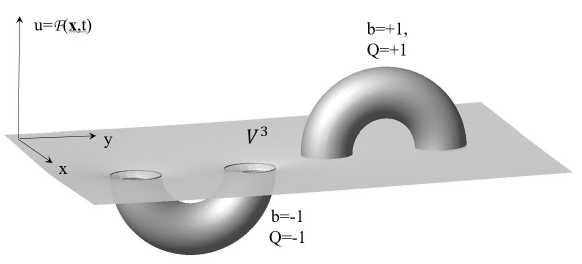
Рис. 4. Структура простейших областей V ³ с ручкой Уилера, в сопоставлении с зарядами протона и антипротона

Более детальный анализ такой классификации [27, 28] указывает на то, что в процессах распада мюона и нейтрона, благодаря слабому взаимодействию, можно усмотреть явное указание на топологическую перестройку границ их областей, соответствующую приведенной классификации. Все это и ряд других соображений [27, 28] говорит в пользу гипотезы о том, что электрический заряд действительно представляет собой топологический инвариант – эйлерову характеристику областей V ³ .

Еще одним важным обстоятельством, связанным с полями D и G. а также уравнениями (5.3) и (5.4), является то, что оба этих поля, с точностью до некоторого скалярного множителя, совпадают с одним и тем же полем:

Действительно:

α

(5.7)

(5.8)

K = — ea.

∂ea j    4^

| e ( x ,t)|3 ’ G 3 |J| '

Это означает, что в предлагаемой теории гравитация и электромагнетизм по сути являются одним и тем же явлением, обусловленным геометрической структурой пространства V 3 , описываемой в терминах геометрических маркеров. Следовательно, в данной теории имеет смысл говорить именно о гравиэлектромагнетизме.

6. Классическая и квантовая динамика. Принцип соответствия

Поскольку масса – это параметр, характеризующий динамику частиц, то для получения достаточно полной модели необходимо рассмотреть то, как в такой модели могут появится уравнения движения материи. Проблему описания динамики можно разделить на две отдельные проблемы. Первая состоит в том, как ввести в теорию такие характеристики движения материальных объектов – частиц, которые бы соответствовали стандартному способу описания, принятому в современной физике. Эта проблема носит название принципа соответствия , обязательному принципу для связывания “старых” теорий с “новыми”. Вторая проблема относится к проблеме выяснения реальных принципов и законов, управляющих движением материи, то есть динамикой гиперповерхности V ³ в объемлющем пространстве R ⁴ .

В [24–27] было показано, что принцип соответствия реализуется с помощью введения поля скорости V переноса маркеров, которое определяется с помощью системы уравнений:

	de a + V a ^ea -0.                                (6.1) dt       dx a                                              ( )
Отсюда однозначно находим:	aα V a < X 't) — -ft de . .

Следствием соотношения является закон сохранения:

dJ + Afv a ∂t ∂x ^α

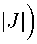
= 0,

(6.2)

который одновременно является законом сохранения массы (5.5). Это позволяет связать с | J| про-

цедуру инвариантного геометрического усреднения по областям V , соответствующим частицам, по

формуле:

I =

У I|J |dV.

V

В частности, частицам можно приписать средние координаты, скорости и ускорения:

α xa|J|dV, Ua(t) = — dt

V

= у V ^a |J|dV, V

A a «- d^- = -/ (^ + v в dv e J x

V

Как показано в [24, 25], соотношение для ускорения можно интерпретировать как уравнение Ньютона для частицы с массой M (5.5), которая движется в усредненном электромагнитном поле:

d²X^t) - eE ^a + [ U x B ] - VU r .

dt ²

Классическое электромагнитное поле вводится формальным соотношением:

V - Vx - Y A ,

(6.3)

где A интерпретируется как векторный потенциал при стандартном условии y — e/m o c (e и mo -заряд и масса электрона, c – скорость света), а χ – как функция действия. При такой интерпретации поле V удовлетворяет тождеству:

dV ^a + V в dV ^a = ∂t       ∂x ^β

e _{E α} m

+ — [ V x B ] + lU r , mc        ∂x ^α

где:

E ^α

дФ

∂x ^α

cAa’

играет роль классического электрического поля с потенциалом Ф, B = rot A - роль индукции классического магнитного поля, а остаточный потенциал U r имеет вид:

U r = ddt + |Ь — Y A | 2 + еФ.

Рассматривая последнее соотношение, как уравнение Якоби классической частицы в электромагнитном поле, и используя преобразование Моделунга [29, 30], находим [24], что функция:

Ф( х ,^) = \ J ,

(6.4)

удовлетворяет стандартному уравнению Шредингера:

где

i h ^ t -

7- ( v- y А?Ф 2m

e еФ + Ug) Ф = 0,

(6.5)

U g = U r -

h² A yJ 2m V IJT ^,

потенциал остаточного взаимодействия, которое можно пытаться связывать с гравитационным взаимодействием.

Полученные соотношения показывают, что введение в теорию поля скорости переноса маркеров и формальное его представление в виде (6.3), а также геометрического усреднения, автоматически приводит к появлению уравнений как классической физики, так и квантовой механики. Таким образом, принцип соответствия воспроизводится в данном подходе в полном объеме, хотя еще требуется распространить все выводы на области, состоящие из нескольких отдельных областей, содержащих экстремумы F. Основная часть принципов рассчета соотношений для сложных областей рассмотрена была в [25].

К этому лишь следует добавить, что представление (6.3) вводит в теорию второй комплект полей, которые должны интерпретироваться как характеристики электромагнитного поля. Поля, связанные с представлением (6.3) и последующими построениями уравнений Ньютона и Шреденгера, были названы классическими. В отличие от этих полей поля D и G следует назвать фундаментальными. Фундаментальная электродинамика не ограничивается уравнением (5.4). Как было показано в [26], из уравнения (6.1) с помощью дифференциальных преобразований можно получить два дополнительных уравнения:

dd D +rot[ D х V ] = —4п £ E k 5( x - x k ) V ,                     (6.6)

k

^ G + rot[ G х V ] = -4nG| J| V .                                 (6.7)

∂t

Первое из этих уравнений фактически является уравнением индукции фундаментального электромагнитного поля, если отождествить поле:

H = [ D х V ] + VФ н ,

(6.8)

с напряженностью фундаментального магнитного поля. Потенциал Ф н при этом позволяет потребовать, чтобы фундаментальное магнитное поле не имело магнитных зарядов, то есть:

div H = div[ D х V ] + АФ _н = 0.

Это уравнение позволяет вычислить градиентную добавку к векторному произведению в (6.8), компенсирующую возможное появление магнитных зарядов.

Второе уравнение в (6.6) можно интерпретировать как уравнение индукции гравимагнитного поля с напряженностью:

Z = [ G х V ] + VФ _G .                                   (6.9)

Для этого поля пока нет экспериментальных требований на отсутствие гравимагнитных зарядов.

Поэтому потенциал ФG пока не определен. Заметим лишь, что напряженность фундаментального магнитного поля и напряженность гравимагнитного поля связаны с общим полем K аналогичными соотношениями, что и D и G:

H = I (JL 3 [ K ^x V + V $ h , G = 4nG IJ l[ K ^x V ] + ^VФ G . | e ( x ,t)| ³                                       3

Еще одним важным обстоятельством всей совокупности уравнений является то, что их общими интегралами движения являются всевозможные величины вида [24]:

I =

11 ( e )| J|dV.

(6.10)

V

В частности, интегралом движения является масса (5.5), которая, с точностью до постоянного множителя, может быть представлена, как сохраняющаяся полная энергия фундаментального электромагнитного поля W в следующей форме:

• 1    Г____. ,         1

  M =

  
  
7.    Расширение геометрии пространства маркеров и темная материя

_4П y(D , ^f )dV = cW.

V

Здесь Фf = -П ^21F F01 j . Последнее соотношение эквивалентно формуле Эйнштейна E = Mc2, что можно рассматривать как завершающий штрих к выполнению принципа соответствия в пред- лагаемой теории.

В дополнение к уже кратко изложенным идеям построения новой теории физических полей и материи, укажем на некоторые важные расширения соотношений, которые позволяют, с одной стороны, дать трактовку некоторым необъясненным эффектам современной физики, а с другой, придать построениям большую основательность, указав некоторые важные числовые характеристики структуры материи, возникающие при таких расширениях. В работах [25, 26] было показано, что способ определения плотности массы материи, возможно, может в реальности быть более общим. Этот вывод можно сделать, учитывая то, что сохраняющимися величинами в предлагаемой теории являются все интегралы вида (6.10). Это означает, что в реальности процедура геометрического усреднения может содержать более общую плотность, чем просто якобиан преобразования |J|. Такой более общей плотностью может быть любая плотность вида:

(7.1)

Р = I^{( e ) | J} |.

Как было показано в [25, 26] все построения оказываются в силе с той разницей, что поле G следует заметить следующим образом:

G = 4П1 ( e )|J | к .

Это необходимо сделать для того, чтобы плотность материи, входящая в уравнение (5.3) для G , содержала дополнительный множитель I ( e ). В [25,26] был предложен способ выбора множителя I ( e ) в виде:

I ( e ) = ^ 1 + R 2 /R 0                                 (7.2)

Здесь R = ^2|F — Fo|, а Ro - некоторая фиксированная величина. Обоснование сводится к тому, что в таком случае интегралы по пространству маркеров эквивалентны интегралам по трехмерным параболоидам, что приводит к появлению добавки к объему пространства маркеров, определяющему массы частиц и механический момент вращения, содержащему числовую поправку, близкую с большой точностью к значению постоянной тонкой структуры. Именно, интеграл по трехмерному параболоиду, соответствующему простой области с одним экстремумом, приводит к следующему объему:

V =3 nRg + R3(1 + 4na),(7.3)

где

Г 3            1 , ,            .      1"|        1                  1

a = Н+8М^ — 1) — а] — 4П = 137.9770423 = О.007247582520.

Это совпадение кажется не случайным.

После такой модификации поля G уравнение для него принимает следующий вид:

divG = 4nGZ (R)p, где P = | J| V1 + R2/R2, а

1 3 + 4R2/R ^{Z ( R )} 3 1 + R ² /R ² '

Этот множитель изменяется в диапазоне от 1 до 4/3, когда R меняется от 0 до R q. Следует отметить, что при любом выборе I ( e ) в уравнении для G будет появляться некоторый множитель, зависящий от I ( e ):

e a д ln I ( e )

.

(7.5)

^{Z( e )} =^{1 +} т ..

Этот факт может служить естественным объяснением эффекта “темной материи” или скрытой массы. Фактически такой множитель можно рассматривать как эффективную гравитационную постоянную G ‘ = GZ (R). Если справедлив выбор функции I ( e ) в виде (7.2), то вариация эффективной гравитационной постоянной внутри области, содержащей один экстремум, не велика и возрастает на больших расстояниях не более, чем на треть от центра области в точке, где F достигает экстремума. Это может объяснить то, почему в локальных лабораторных экспериментах отклонения от G не обнаруживаются, но на больших масштабах это может приводить к эффективному возрастанию массы до достаточно больших значений.

8.    Как описывать динамику материальной гиперповерхности V 3?

После того, как способ описания физических полей, как проявлений геометрии и топологии гиперповерхности V ³ , согласован с предыдущими теориями, кроме возможно ОТО и частично СТО, необходимо поставить вопрос о том, какие физические законы управляют динамикой этой гиперповерхности, как элемента объемлющего пространства. На это вопрос оказывается ответить гораздо сложней, чем добиться выполнения принципа соответствия. Поскольку прямых экспериментальных фактов относительно свойств V ³ , как материального объекта объемлющего пространства R ⁴ нет в современной физике, то приходится опираться на некоторые косвенные соображения, которые могут помочь в построении полностью замкнутой теории.

В физике в рамках классической физики рассматривались задачи, в которых приходилось описывать динамику двумерных поверхностей под действием внутренних и внешних сил. К таким задачам относятся задачи динамики упругих мембран и границ раздела двух непрерывных сред, например, границы раздела вода-воздух, либо задачи с комбинацией этих двух моделей. Исходя из этого, можно пытаться строить модели динамики V ³ , либо как границы раздела двух сред, заполняющих собой объемлющее пространство R ⁴ , либо пытаться описывать V ³ как упругую мембрану, возможно взаимодействующую с окружающими ее средами, подобными жидкости или газу. Такой путь кажется вполне разумным, однако он наталкивается на несколько существенных трудностей, которые необходимо преодолеть, прежде чем удастся выписать подходяще уравнения.

Некоторые соображения относительно свойств уравнений динамики V ³ были высказаны [24–27]. Приведем их здесь, чтобы завершить изложение нового подхода к описанию материи с помощью геометрии в сравнении с некоторыми постулатами ОТО.

Во-первых, для получения замкнутого описания геометрии V ³ , как элемента R ⁴ , необходимо указать уравнение для одной функции F , вместо шестнадцати уравнений Эйнштейна в ОТО. В окончательной теории таких уравнений может быть больше, чем одно, поскольку для описания динамики придется включать в общую схему некоторые параметры “ультраматерии”, которая заполняет собой пространство R ⁴ . Однако фактом остается то, что для построения геометрической структуры V ³ , в конечном итоге, требуется знание только одной функции F .

Во-вторых, уравнение для F, как функции координат на P ³ ∈ R ⁴ , должно допускать многозначные решения. Это условие не обязательно свидетельствует о том, что уравнение для F должно быть нелинейным. Как было показано в работах [39, 40], многозначными решениями обладают и линейные уравнения гиперболического и эллиптического типа и некоторые типы параболических уравнений [41]. Однако можно предположить, что в конечном итоге, уравнение для F должно быть нелинейным, поскольку только нелинейность обеспечивает появление локализованных волновых образований, которые могут быть сопоставлены частицам. Соображения многозначности, с целью пытаться угадать вид подходящего уравнения, были рассмотрены [27].

В-третьих, структура уравнения для F должна содержать оператор Д’Аламбера, который обеспечивал бы существование волновых решений типа электромагнитных волн, которые наблюдаются в широком диапазоне масштабов. Вместе с тем, это уравнение должно содержать дополнительные слагаемые более высокого порядка по производным вдоль координат. Наличие таких производных необходимо для того, чтобы волновые, незатухающие решения существовали лишь вплоть до некоторой минимальной длины волны λ0 . Такое ограничение вытекает из того, что в теории имеются топологические структуры типа ручек Уилера не всех возможных масштабов, а только больше некоторого фиксированного масштаба, который, по необходимости, должен быть связан с λ0 . Такое же ограничение вытекает из объяснения существования только трех типов нейтрино и, вообще говоря, других типов частиц, которое было предложено в рамках данной теории в работе [27]. Действительно, каким бы ни было уравнение для F в пределе малых возмущений, оно должно линеаризоваться, но так, что возмущения с масштабами меньше λ ₀ должны затухать. В противном случае могли бы существовать и структуры с меньшим масштабом, но конечной амплитуды. По крайней мере, такой вывод кажется вполне логичным. Примером уравнения, который подходит под эти критерии , является уравнение вида:

F tt = c2AF + ct AA F + H (F).

Здесь c – скорость света в вакууме, σ – некоторый положительный параметр. Некоторая функция H(F ) введена для иллюстрации возможной нелинейности рассматриваемого уравнения. Если отбросить нелинейность, считая ее малой, и рассмотреть малые волновые возмущения, то дисперсионное уравнение, связывающее частоту ω волн и волновые числа k будет иметь такой вид:

ш ² = c ² | k |2 — ст| к | ⁴ .

В случае ст >  0 вещественная частота существует только до некоторого максимального волнового числа к о = с/^. Следует отметить, что такого типа уравнения можно получить, если рассматривать в качестве модели V ³ упругую бесконечно тонкую мембрану, взаимодействующую с окружающей ее веществом типа жидкости или газа, но в размерности пространства 4, а не три, как это принято обычно в теории упругости [42].

К сожалению, эти общие соображения не позволяют пока указать путь вывода требуемого уравнения для F . Возможно, было бы полезно пытаться угадать не само уравнение для F , а принцип его вывода, подобный вариационному принципу наименьшего действия, учитывая все соображения высказанные выше. Так были получены уравнения Эйнштейна в ОТО. Однако такой путь также требует знаний каких-либо свойств гиперповерхности V ³ и окружающей ее “ультраматерии” в объемлющем пространстве R ⁴ . Конечно, многие проблемы разрешились, если бы в нашем распоряжении появилась информация о том, что из себя представляет материя, из которой состоит гиперповерхность V ³ . Однако современный эксперимент пока не может предоставить такую информацию в распоряжение теоретиков.

Заключение

Общая Теория Относительности проложила путь к совершенно новому подходу в физике на то, как можно успешно описывать свойства материи и полей, опираясь на свойства неевклидовой геометрии пространства-времени. Она подтолкнула физиков и математиков строить очень сложные модели и материи, и пространства, отыскивая способы их связи с реальным экспериментом. Можно сказать, что ОТО явилось предтечей новых теорий, которые пытаются решать задачи физики в целом, соединяя все ее части в одну общую теорию полей, материи и пространства. Фактически, благодаря ОТО, появились в физике такие концепции, как теории Великого объединения. Однако в процессе реализации таких объединяющих идей выявился целый ряд проблем общей концепции ОТО, что послужило основой для множества попыток построить ее обобщения, которые бы решали хотя бы часть этих проблем.

Основным выводом данной работы может служить указание на то, что для построения теории, которая бы включала в себя электромагнитное и гравитационное поля, частицы с электрическим и барионным зарядом, и даже “темной материи”, может служить представление о том, что в основе всех этих явлений лежит геометрия и топология трехмерной гиперповерхности, вложенной в евклидово пространство размерности 4. Как оказывается, для того, чтобы связать с этой геометрией все современные атрибуты материи – электрический заряд, массу, барионный заряд, электромагнитные и гравитационные поля и, наконец, свойства квантовых объектов, достаточно ввести понятие геометрического маркера. Дифференциальные соотношения, связывающие эти маркеры с геометрией через свойства функции высоты физической гиперповерхности, приводят к полному набору уравнений классической и квантовой механик в нужном их сочетании, основанном на процедуре усреднения по пространству. Такое усреднение носит нестатистический характер, а именно – геометрический, что снимает ряд вопросов относящихся к “иррациональности” некоторых аспектов квантовой теории. Таким образом, предлагаемая теория может рассматриваться как претендент на роль теории материи, объясняющей множество экспериментальных данных и наблюдаемых явлений. Тем не менее, как обсуждалось выше, теория не может считаться законченной, поскольку в ней отсутствует такой важный элемент, как уравнение динамики самой физической гиперповерхности в объемлющем пространстве. Без этого уравнения все выведенные в теории соотношения выражают лишь тождественные связи между отдельными элементами описания геометрии и ее динамики. Установление принципов такого описания является следующей основной задачей построения законченной на данном этапе теории геометрического описания материи.