Mathematical description of Euler disk and experiments with him
Автор: Solomon I. Khmelnik
Журнал: Доклады независимых авторов @dna-izdatelstwo
Рубрика: Physics
Статья в выпуске: 52, 2021 года.
Бесплатный доступ
It is pointed out that at present there is no complete theory of the Euler disk. A complete mathematical description of the Euler disk in statics is given. Some experiments are described.
Короткий адрес: https://sciup.org/148323941
IDR: 148323941
Текст научной статьи Mathematical description of Euler disk and experiments with him
The classical theory does not allow one to explain the behavior of the Euler disk without invoking additional forces. In [1] it is shown that taking into account the influence of air also does not allow finding an acceptable explanation. Hope is pinned on the effect of sliding friction, but there is no strict solution, and intuitive hopes only for this friction are poorly substantiated - see, for example, [2]. There is, apparently, no explanation for the transition from rotation of the disk around the vertical diameter to rotation in a circle in an inclined position. If the disc slides in a circle, then it is apparently necessary to take into account also the centrifugal force. But, the main thing that surprises us is why the disc does not fall, but rotates long enough?
Below is an attempt to find answers to these questions. The article is a revised version of article [6]. We warn the reader in advance that the answers were obtained on the condition that the centrifugal force and the
Coriolis force are real, and not fictitious, forces. A mathematical proof of this fact is given in [3].
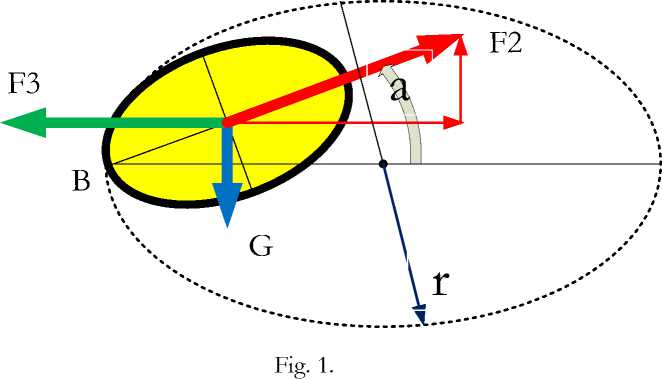
In fig. 1 shows the Euler disk. Table 1 of Appendix 1 lists the parameters of the state of the disc at the initial moment 1 and at the moment 2, when the disc is in a position at which the angle a< я/2 . The definition of these parameters is given in Appendix 1. At moment 1, there is only rotation around the vertical axis of the disk. At moment 2, partial rotation appears additionally. The force of gravity mg also appears, the vector of which passes the point of rotation O. Because of this, a decrease in the potential energy of the top appears
WP = mgh(1 — sin a) (1)
-
- see the formula or (clause 2.7) in Appendix 2.
We write for moment 2 the equations of the laws of conservation of momentum L and energy W , which do not depend on how and by what forces the disk entered this state:
Lz + L4 = Lx,(2)
Wz + W4 + Wp = W,.(3)
Substituting the equations from table. 1 into equations (1, 2), we obtain: /2)2 + /з<°3 = /1<°1,
4/2^2 + 4/3) + Wp = ^o)?.(5)
where 0) 1 , 0) 2 are the angular speeds of rotation of the disk at times 1 and 2, 0)3 is the angular speed of partial rotation. From (4) we find:
|
0 3 = J^Q 0 1 — 0 3 ) . (6) |
|
|
Substit |
uting (6) into (5), we find: ^«^ + jA^G ® i -® z )) + W , = j^ W i . (7) |
|
Appen |
dix 2 shows (see (item 2.9)) that w , = qbO (8) |
|
where obtain: |
q is a constant - see (item 2.10) in Appendix 2. From (7, 8) we |
|
4/2 0 2 + 4 J 3 03 + qhj 2 0) 3 = ^ j^ |
(9) |
|
We denote |
|
|
__ J2 l , J 3 |
(10) |
|
b = (1 + 4qa) . |
(11) |
|
Then from (9, 10, 11) we get: |
|
|
aco 3 + b0 3 = ao 2 . |
(12) |
|
From (10, 6, 12) we find |
|
|
ao 2 + b(o 1 — o3)3 = aw3 , |
(13) |
|
or |
|
|
(b + a)o 3 — 2bo 1 o3 + (b — a)co 1 = 0 , |
(14) |
|
Solving (14), we get: |
|
|
° 3 bi: 'b ± “> • |
(16) |
|
It follows from experiments that 03 ^0 1 . Then |
|
|
( b-a) 02 = x Oi . 3 (b+a) 1 |
(17) |
|
From (6, 17) we find |
|
|
/1 \ a(3a-b) ° 3 = l(- ° 1 ° 3 ) = 3(b+a) ° 1 . |
(18) |
|
From (18) we find |
|
|
3(b+a) Oi — , . 03 . 1 a(3a-b) 3 |
(18а) |
|
From (18а, 17) we find |
|
|
(b-a) 3(b+a) 3(b-a) |
(18b) |
|
0'2 -- z, X , , X 0'2 -- , , , 0'2. 3 (b+a) a(3a-b) 3 a(3a-b) 3 |
The disc is tilted by gravity mg. The transformation of this energy into the kinetic energy of the rotational motion of the top occurs due to the fact that in the process of falling on it, as is known, the Coriolis force F1 acts, which creates a torque and the corresponding angular velocity of precession 03.
The fall of the disk is counteracted, as you know, by another Coriolis force F3. The disc falls very slowly. This means that the force F3 is approximately equal to the force of gravity - see Appendix 2. Obviously, with such deceleration, the source of this force consumes energy approximately equal to WP. Therefore, there is a source of energy for this force. But this assumption is thwarted by the persistent modern view that the Coriolis force is a fictitious force. And a fictitious force cannot deliver energy ...
3. Disc sustainability
In Appendix 2 it is shown that for some ^=^ о the Coriolis force F 2 balances the horizontal centrifugal force F 3 and the vertical gravity mg -see (item 2.3) and (item 2.5).
Until this speed is reached, the disk gradually falls under the action of the force F4 , determined from (p2.6a) and calculated as a result of the interaction of the Coriolis force and the force of gravity. When F4 = 0 , the fall process stops. But for this, the disc must start to fall.
At K= 0 it is seen that F4 = mg . But this force is directed vertically and cannot cause falls. Thus, to start the fall, an external force must bring it out of its vertical position.
4. Conclusions
So, the action of the Coriolis forces leads to the fact that
-
• when the disk falls, it loses the kinetic energy received during launch, but replenishes it due to potential energy;
-
• there is such an inclined position of the disk, in which the Coriolis force balances the horizontal centrifugal force and vertical gravity;
-
• in this position, the kinetic energy of the disk remains unchanged and equal to the kinetic energy obtained during launch;
-
• the fall of the disc from the specified stable position is caused by a gradual decrease in its kinetic energy due to deceleration;
-
• the slow fall of the disc is due to the braking due to the second Coriolis force, which must consume energy for this (like the braking engine of a descending satellite),
Such an action of these Coriolis and centrifugal forces is possible only if they can do work, i.e. are real powers. This proves the reality of these forces. On the other hand, a mathematical proof of this fact is given in [1]. It is shown there that these forces can be substantiated as a consequence of Maxwell's equations for gravitomagnetism, and the source of energy for this force is the Earth's gravitational field. But even in the 68
absence of such evidence, there are many doubts in the assertion that these forces are fictitious [2].
In Appendix 2 it is shown that the inequality r > R follows from the equations of the disk. Modeling shows that for r > R there is a certain angle K, where all parameters of the disk state take an infinite value. Thus, the condition r = R. (19)
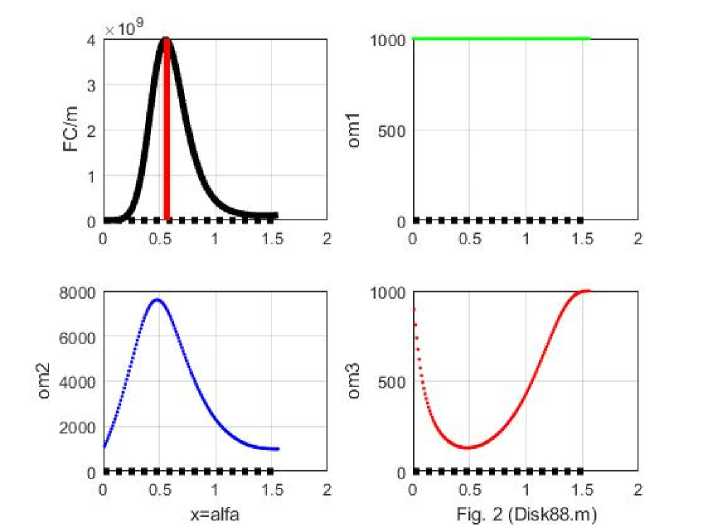
The above equations make it possible to find all the parameters of the disk for a given m and R. In table. 1 shows some examples in system SI. The graphs of the functions 0)1 , 0)2, 0) 3 and the specific Coriolis force F2/m at 0) 1 = 1000 and R = 0.25 are shown below - see Fig. 2. It can be seen that there is a sharp maximum at OC~ tt/2 , where the Coriolis force takes the greatest value. At this point, the disc remains in a stable state for a long time - see fig. 3 from [5].
Another experiment is considered in Appendix 4, where it is shown that the considered forces act on each element of the disk.

Fig. 3.
Appendix 1
Here we will determine the parameters of the state of the disk at moments 1 and 2. In table. 1 shows the basic formulas, where the following designations are adopted
m is the mass of the disk, g is acceleration of gravity, mg is gravity,
R is the radius of the disk, h is the height of the center of the disc - see fig. 1,
0)1 is angular velocity of rotation of the disk around the vertical diameter at the moment 1,
0 2 is angular speed of rotation of the disk around the vertical diameter at the moment 2,
0 3 is angular velocity of partial rotation at moment 2,
V is linear speed of precession,
J is angular momentum,
W is energy.
From fig. 1 follows:
h = Rtg(K). (п1.0)
From table. 1 follows:
CL = — = 1/1.5, (п1.1)
/з 4 7
The linear speed of precession is the speed of movement of pixel B at the radius AB, rotating with the angular speed O 3 (see Fig. 1):
V = 03 (r — Rcos(«)). (п1.3)
Table 1.
|
Angular speed |
Moment of inertia |
Moment of momentum |
Kinetic energy |
|
|
Rotation of the disc around its own vertical axis |
0)1 |
/1 =4 mR2 |
L 1 = J i ° i |
И7 1 =2 L 1 O 12 1 7 = 8 A° 2 |
|
Rotation of a disk inclined at an angle К to the plane around the proper axis |
o2 |
1 / 2 = ^ mR2 |
L 2 = J 2 O 2 |
И/ 2 =2 L 2 W 2 1 2 = 4 J 2 ° 2 |
|
Partial motion of a top inclined at an angle К to the plane . |
o3 |
J 3 = J 2 + mR2 (Steiner's theorem) J3 = a - mR2 , when a = 1.5 |
||
|
, , 1 ,2 L3 = J3O3 = 2c mR o 3 |
||||
|
W 3 = 2 L 3< ° 3 1 2 = 4 J 3°3 = 1 . . = 4cmR2o 2 |
||||
Appendix 2
The fall of the disk is counteracted by the Coriolis force.
F2 = — 2mw2 x v, (п2.1)
where V is the linear speed of precession (p1.3), and the centrifugal force
F3 = —mo)2(r — Rcos(K)) (п2.2)
In the steady state, the force F 3 and the force of gravity mg are balanced by the force F2 - see fig. 1. Therefore, from (item 2.1, item 2.2, item 1.3) we find:
F2 = - Sinlfe) = "'‘"з(т — ??cos(к))/sln(к), (п2.4)
mg = —F2cos(k) = mco2(T — Rcos(K)) • ctg(K) (п2.5)
or
g = "3R (K — cos(K)) • ctg(K). (п2.6)
If this equality is not satisfied, then the disk falls under the action of the force determined from (item 2.5):
F4 = mg — mtn2(T — Rcos(K)) • ctg(K) (п2.6а)
It is seen that the solution to this equation exists only for
T>R . (п2.6 а ).
Consequently, condition (п2.6 а ) is always satisfied for the Euler disk.
When tilted at an angle K , the disk is displaced vertically by
R(1 — sin k) and, therefore, loses potential energy
WP = mg R (1 — sin k). (п2.7)
Combining this formula with (item 2.6), we find:
WP = m Next, we will combine this formula with the formula for J2from table. 1. Then we find Wp = ^m^1 R2 (^ — cos(K)) ctg(K)(1 — sin k). or where wp = qJ2 "2 (п2.9) (п2.10) q = I (^ — cos(K)^ ctg(K)(1 — sin k). Appendix 3 Here we will consider in more detail the Coriolis force F2, determined by (п2.1): F2 = Im^^^R (^ — cos(K)), (п3.1) From (item 3.1, 18b) we find f2 = —|mco|R (R — cos(«)) ш1 ^§^ (пз.2) or F = — Im.2R j T — cos(K)i.2 — (2(^±^! 2 3 V? v J 1a(3a —6) \a(3a-b)) or F2 = —2m602 Rdf, (п3.3) where df = 2 (R - cos(«)) (b — a)(b + a)2 ,/■':. (П34) Appendix 4 An experiment is known from the Internet, shown in Fig. 4. "Chain circle" - the CC spins up on a cylinder at high speed and collides from this cylinder. In this case, the CC continues to move like a Euler disk, retaining its shape. Here, forces A and B act on each link in the chain. From the previous it follows (see Fig. 1) that the force F2acts in the direction of the vector A, and the force F3 acts in the direction of the vector B. In addition, centrifugal force F5acts on each link of the chain, caused by the rotation of the CC around its own axis. This force is added to the force F2and ensures that the CC remains in shape. Thus, A = F2+F5and В = F3. Both of these forces keep the CC from dropping. This means that the considered forces act on each element of the Euler disk, and in this case, on the links of the chain. Fig. 4.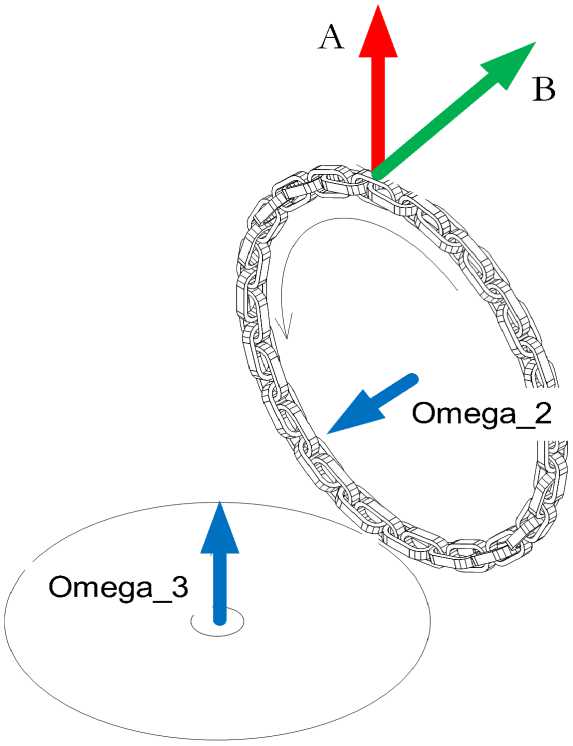
Список литературы Mathematical description of Euler disk and experiments with him
- Dynamic effects of the Euler disk, NONLINEAR DYNAMICS, 2008, V. 4, №1, pp. 99–104, http://elibrary.udsu.ru/xmlui/bitstream/handle/123456789/6767/Zamechatelyie.pdf?sequence=1
- Euler's disk, https://thexvid.com/video/8xIfylbpR3s/%D0%B4%D0%B8%D1%81%D0%BA-%D1%8D%D0%B9%D0%BB%D0%B5%D1%80%D0%B0.html
- S.I. Khmelnik. Coriolis Force and centrifugal force in electrodynamics and mechanics. The Papers of independent Authors, ISSN 2225-6717, Volume 49, 2020, https://zenodo.org/record/3900260.
- Astakhov A.A. Physics. The order of things or awareness of knowledge, 2006, https://www.litres.ru/a-a-astahov/fizikadvizheniya-alternativnaya-teoreticheskaya-mehanika-iliosoznanie-znaniya/chitat-onlayn/ (in Russian)
- The Maths of Spinning Coins and Euler's Disk, https://www.youtube.com/watch?v=8pSLffliCk0
- S.I. Khmelnik. Mathematical description of the Euler disk, The Papers of independent Authors, ISSN 2225-6717, 2020, 50, 75–83 (in Russian) http://doi.org/10.5281/zenodo.4047923


