Mathematical model of the dynamics in a one nonholonomic vibration protection system

Published Online October 2018 in MECS

The investigation of the problem considered in this article is due to the fact that recently a large number of seismic and damping devices have appeared, the effect of vibration protection of which is based on the use of special bearing supports that realize nonholonomic ties. In such systems, the effect of vibration protection is achieved by providing significant relative displacements of incommunicable bodies with rolling without sliding along the supporting surfaces of mobile bearing bodies [7 – 12, 17 – 19, 21 – 23]. In this case, the motion of the supporting bodies is either specified as a function of time, or completely determined by the joint motion of a system of coupled solids.

Prior to this, the close problems of nonholonomic mechanics [8 – 9, 14 – 15] on the rolling of a heavy homogeneous ball without sliding along fixed surfaces of the second order (sphere, horizontal and vertical cylinders, vertical cone and paraboloid of revolution, triaxial ellipsoid) are of theoretical importance. In [4 – 6], the dynamic effects that arise when the ball rolled along a plane and a sphere rotating about a vertical axis were investigated. In [10, 13, 17 – 19], problems of the dynamics of rolling systems with practical value were investigated. In the books [1, 8, 20] formulas are derived for determining the natural frequency of the plane oscillations of a homogeneous sphere (cylinder) in a stationary spherical (cylindrical) recess. Also, roller absorbers are successfully used to suppress the so-called "dance" (galloping) of wires of powerful power lines, as well as for seismic protection of buildings [8]. In work [10] dynamic behavior of ball shock absorbers of longitudinal shocks was studied in the complex transport system, which are used on railway platforms for the carriage of particularly fragile loads. In [16], the formulation of the problem of controlled motion of a thin homogeneous disk, which rolls along a horizontal plane without slip, is considered. This problem is formulated and solved in the framework of the theory of optimal control. In the reports [12, 21, 22] of Chinese scientists, the results of studies on the effectiveness of the effect of roller absorbers (VBA type) on the level of dynamic loads acting on the blades and racks of powerful wind farms are presented. In work [23], some basic drawbacks of ball absorbers of VBA type in the region of vibration damping of low-frequency oscillations of flexible high-altitude structures were noted.

As can be seen from this short review, roller absorbers and shock absorbers are in demand in various fields of technology and the national economy. The tasks of damping vibration, associated with their study and use, are new, diverse and topical from a scientific point of view.

• II.    Statement of the Problem

The motion of a homogeneous heavy ball without sliding along the inner surface of a movable spherical cavity of the supporting (carrying) body is considered. In this case, the motion of a supporting body with a spherical cavity in space is carried out translationally in accordance with the given functions of time – translational movements of the vertex of the indicated spherical recess (Fig. 1).

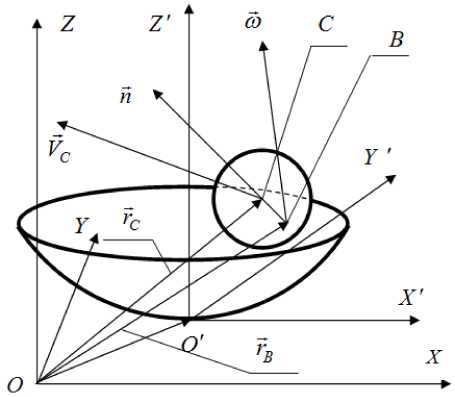
Fig.1. Homogeneous ball in spherical groove of the supporting body

The peculiarity of the present study is that the spherical excavation of the supporting body has the ability to move translationally in space in accordance with specified functions of time x ₀( t ) , y ₀( t ) and z ₀( t ) , and which can be regarded as specified movements of the carrying body.

The purpose of the paper is – 1) on the basis of Appell's nonholonomic mechanics to construct kinematic and dynamic equations for the motion of a heavy ball in a spherical cavity without slipping, taking into account the translational motion it prescribes in space; 2) Using the differential equations obtained, a numerical experiment is performed to study the dynamic behavior of the ball motion.

• III.    Geometric Relations and Nonholonomic Ties Equations

We introduce two coordinate systems: fixed OXYZ and movable O^'X^'Y^'Z^' , connected with the top O^' of the spherical recess. Let us write the equation of the surface of the recess in the system of axes O^'X^'Y^'Z^' :

( xB ) ² + ( yB ) ² + ( z B - R ) ² = R ², z '< R ,     (1)

where R is the radius of the spherical recess; xB , yB , zB - coordinates of the contact point of the ball and the spherical recess (point B ).

Using equation (1), we define the expression for the unit normal vector n to the inner surface of the spherical recess at the point B .

n = ^- -1 • ( xB ; yB ; ^z B - R )              ⁽²⁾

R

We also write the expression for the first derivative of the unit normal vector n in the case of translational motion of the supporting body. Differentiating expression (2), we obtain:

n = ^- -1 • ( ^xB ; ^y B ; ^zB )

R

The radius vectors r_B and r_C are related by the following geometric relationship (Fig. 1):

rc = rB +r • n, where r is the radius vector with the origin at the point O and the end at the point B whose coordinates are defined as follows:

rB = (xo+xB; Уо+yB; zo+zB)

We differentiate equation (4) in time:

VC = rB +r • n(6)

We rewrite (6) in a scalar form with (3):

X ^е с = X^е O ⁺ a • X c _B;

y c = y o+ a •y b;(7)

zc = zo+ a •zB, where a = 1 - r/R . It is obvious that for r = R ^ a = 0 and the relative motion of the ball is not realized.

The vector kinematic relation (the equation of nonholonomic ties), which determines the absence of slip of the ball relative to the spherical recess at the point B of contact, has the form:

VC = VB + S x r • n ,               (8)

where V_B = r?_B .

From equations (6) and (8), after certain transformations, we obtain the differential equations of a nonholonomic ties in the scalar form:

xc = ^xo ^{+ a} ^[® Y •( ^z B ^{- R} ) ^{- s} z ■ y B ] ;       (9)

^yc = ^yo ^{+ a} -[ ^s z • ^xB ^{- ю} х •( ^zB ^{- R} ) ] ;     ⁽¹⁰⁾

^zC = zO + ^a ' ( ® X • yB ^- ГО • ^xB )         ⁽¹¹⁾

• IV.    Construction of the Equations of Motion of a Heavy Ball in a Movable Cavity

The construction of the dynamic equations of motion of a ball in a moving spherical cavity will be performed using the Appell’s approach for nonholonomic systems [14, 15].

Let us write in a general form the function S - the energy of the accelerations of a heavy ball in the motion under consideration:

S = — - ( x 2 + y 2 + z 2 1 + J • (^ 2 + ГО 2 + ^ 2\   (12)

CCC   X Y Z where m is the mass of the ball; r - is the radius of the ball; J - is the moment of inertia of a homogeneous ball with respect to its center of mass at the point C (J = 0,4 - m - r2).

We define the second derivatives of the coordinates of the center of mass of the ball in (12), using the once-differentiated equations (9) - (11).

xc = xo + a-[^Y •(zB -R)-®z ■ УB] + Fx ;

yc = yo + a-^toz - xB -®X •(zB -R)J + FY;

zC = zO + a-(^x • yB -®Y - xB) + Fz, where

Fx = ^a- ( ® Y • zB - ® z •^yB ) ;

^fy = ^a- ( ^a z ■ ^xB ^- ® x ■ zB ) ;

^FZ = ^a' ( ® x •^y B ^- ГО • ^XB ) .

We substitute the obtained expressions (13) – (15) in (12) and take into account only that part of the acceleration energy S , which depends only on the accelerations ГО _х , ro Y , ro _z . We denote it S * .

* f J m 2       \2           n\2 |    2

S =|^ + y-a ’L(yB) + (zB -R) ]j-rox + f J m 2 r \2   / , n\2 “A .2

j“ ⁺ ~^{- a -} L ⁽ x B ) ^{+ (} z B ^{- R} ) Jj ^- ^Y ⁺

. f J m    2 Г/ 1 \2       , \2 "|1   .2

⁺ |^ ⁺ y ^{- a -} L ^{( y}B ) ^{+ ( x}B ) ^J j' ^ro Z ^-

• ^- m ^{- a} 2 ^- yB ' ( zB ^- R ) ^- ^ Y ^ ^Z ^-

• - m - a ² - xB • ( zB - R ) - ГО _х ro z_z -

• - m - a xbB • yB • rox • roY +

^{+ m} '«• [ yB • ( zo ^{+ F}z ) ^- ( ^yo ^{+ f}y ) • ( zB ^- R ) ]• ^ro x ⁺

+ ^{m a} ■ [ ( xo ⁺ Fx ) ' ( zB ^- R ) ^- ( ^FZ ^{+ z}o ) ' ^xB ^J- ® Y ⁺

+ m ^a- 1^( ^yo ⁺ FY ) ' xB ^- ( xo + Fx ) ^- yB ]' ^ro z .    ⁽¹⁶⁾

We write Appell's equations in a general form:

d S l _ n . d S * _ _p   s s *

= PX;   .  = PY,   .  = PZ дГОх       uCOy      OG^z

We differentiate expression (16) in accordance with (17):

d s               2 r_n2      \2"|

—;— = { J + m - a -1 R - ( x b ) I } - ГО х - дГО х                ^[            JJ

- m - a ² - xB • yB ro Yy - m - a ² - xB • ( zB - R ) ' ro _z +

^{+ m - a -} [ yB ^- ( ^F _z ⁺ zo ) ^- ( ^yo ^{+ f}y ) ' ( ^zB ^{- R} ) ] ;   ⁽¹⁸⁾

Ц *- { ^{J +} m ^{- a 2 -} [ ^{R 2 - ( yB ) 2} ] }- «Y -

- m - a ² - yB • ( zB - R ) ' to _z - m - a ² - xB • yB * ro _x +

+ ^ma- [ ( ^xo ⁺ Fx ) ' ( zB ^{- R} ) ^- ( ^Fz ^{+ z}o ) ^{- x}B ] ; ⁽¹⁹⁾

dS *  X. 2

---= <  J + m a dro _z   I

^- [ ^{R 2 -}( ^zB - ^{R ) 2 J} } ^ zz ^-

- m a 2 - y B •( zB - R ) - ro Y - m -0 2 x b B •( z B - R ) - ro _x +

+ m °- [ ( ^yo + FY, ) ^{- x}B ^- ( ^xo + Fx ) ^- yB ]      ⁽²⁰⁾

To determine the right-hand sides of Appell's equations, we introduce the quasicoordinates n _x , n _Y , n _z , where ro _x = n _x ; ro Y = n _Y ; ro _z = n _z . We write down the expression for elementary work δA, considering the motion of the ball under the action of gravity on virtual displacement 8z_c . Here, the work of the nonholonomic ties reaction is zero, since the virtual displacement is zero because of the lack of slip of the ball with respect to the spherical recess.

d A = - m - g x zc_c              (21)

We define the virtual displacement taking into account the third scalar equation (11) of nonholonomic ties:

S z_c = a - ( y B • 5n _x - x B • Sn _Y ) (22)

On the other hand, the expression for the elementary work of δA in terms of generalized forces PX,PY,PZ , referred respectively to independent quasicoordinates nX, nY, nZ , has the form:

S A = P_X • Sn _X + PY • Sn _Y + P_Z • Sn _Z     (23)

Using equations (21) - (23), we obtain expressions for generalized forces (the right-hand sides of Appell's equations):

P x = — a - m - g - yB ; P y = a-m • g - xB ; P z = 0   (24)

We substitute the expressions (18) - (20) and (24) into Appell's equations (17). After carrying out some transformations, we obtain a system of differential equations with respect to to ^, to , to_z :

D ^to X , to , to _Z ] T = BT ,           (25)

where the elements of the matrix D have the form:

• ^d 11 =      + R ^{R —(} xB ) ; ^d 12 ^{= —} xB * ^yB ;

m -a

• ^d 13 =- xB •( ^zB ^{— R} ) ; ^d 21 = ^d 12 ;

• ^d 22 =---- 2 ^{+ R} 2 - ⁽ yB ^{) 2} ;

m -a

• ^d 23 = ^{— y}в ’^{( z}в ^{— R} ) ^{; d} 31 = ^d 13 ;^d 32 = ^d 23^;

• ^d 33 =---- 2 ⁺ R ² - ( ^zB - ^R ) ^2,

m-a and the elements of the column vector BT are determined by the following expressions b1 = a"x • [(yo+FY) • ( zB — R)— yB •( g+zo+Fz) J;

b 2 = ^a "1 •[ xв • ( g + zo + Fz ) ^— ( xo ^{+ f}x ) • ( ^z B ^{— R} ) J ;

b3 = a1 •[yB •(xo + fx)-xB •(yo + fy)]

We express the accelerations d)_x, d)_Y, d)_z from the system (25):

to = Q- b; to = Q- b2; toz = Q• Ьз(29)

( JY where Q = I----- + R I , a ^ 0 or r ^ R.

V m-a

Let us free ourselves from the derivatives XC ’B, y ’B, :l’b in the right-hand sides of expressions (29) for b . To this end, we use equation (6), on the left-hand side of which we take into account the kinematic relation (8):

xв = toY •	( z'в	— R )-	- to z	• yB ;	(30)
yB = to Z	• x'в	- to X	• ( zB	— R ) ;	(31)
zв =	to X	• yB —	■ toY •	xB	(32)

We write down the differential equations of motion of the ball in quasi-coordinate fields after the indicated transformations:

^to x = P ^- { ^yo • ( ^zB ^{- R} ) - ( g ⁺ zo ) • yB } ⁺

+p-(R - r )• ®„ •[ yв ^>г-(zB -R )• ®y J;

® Y = P ^- { ( g ^{+ z}o ) • ^xB ^- xo • ( ^zB ^{- R} ) } ⁺

+p-(R-r)• to, •[(zB-R)• tox-xB• tozJ;

^to z = P ^- [ ^xo • yB ^- yo •^xB ] ⁺

+P-( R-r )-ton •(xB • toY - yB • toX ) , were p =

________ R - r ________

R • ( R ² + 2 • R • r + 1,4 • r ² ) ^;

to, = ^- R ¹ • [ to x •^x B ⁺ ® Y ■ y B ^{+ to} Z ■ ( ^zB ^{- R} ) J .

For a complete description of the motion of a homogeneous heavy ball in a moving spherical cavity to the system of differential equations of motion (33) - (35), it is necessary to attach a system of kinematic equations (30) - (32) that describe the trajectory of the ball trace on the surface of a spherical cavity in space and time (in the movable axes o’XYZ’ ).

The problem under consideration admits the construction of an energy conservation integral with allowance for the translational motion of the spherical cavity in space. To find it, we multiply each of the equations of the system (33) - (35), respectively, by to _X , to _Y , to _Z and add them to each other. As a result, we obtain the following equation:

to _X *to _X + toY • to _Y + to _Z • to _Z =

= ( g ^{+ z}o ) ^- ( ® Y •^xB ^{- to} X • yB ) ⁺

^{+ x}o •[ yB "  ^to Z ^- ( ^zB ^{- R} ) • ^to Y J ⁺

^{+ y}o •[ ( zB ^{- R} ) • ^to x ^{- x}B • ^to z J .         ⁽³⁶⁾

We transform the right-hand side of equation (36) taking into account the equations of system (9) - (11) thus:

to X to X + to Y to Y + to Z to Z =

x O * x O ⁺ y O ■ y O ⁺ z O ■ z O ^— x O ■ x C ^— y O ■ y C ^— z O ■ z C ⁺ g ' z O ^— g ■ z C R ² - 2 • R • r + 1,4 • r ²

We integrate equation (37), multiplied by the mass of the ball m . After some transformations, we get:

m •( R2 — 2 • R • r +1,4 • r2 )• — =

= m • x O ⁺ y O ⁺ z O

—

m • g • z_C + m • g • z_O — J m • X_O • dx_C —

— J m • y_O • dy_C — J m • z_O • dz_C + const ,

where to2 = toX + aY + toZ.

Now we write the indicated energy conservation integral:

m •( R2 — 2 • R • r +1,4 • r2 )•to +

+m • g • zC

„ xO + yO + zO

— m--

— m • g • zO

—

—J fXn • dxC — J fYn • dyC — J fZn • dzC = const,

The parameters of the dynamic system and the specified displacements of the spherical cavity were selected as follows: R = 3,0 m; r = 0,2 m; A = 0,2m; B = 0,2m; C = 0,1m; § 1 = 0,5; ^ ₂ = 5,5 ; ^ ₃ = 0,1; to 1 = 2 rad / с; to ₂ = 1rad / с ; to 3 = 0,5 rad / с .

The integration of the resulting system of differential equations was carried out for zero, initial values of the unknowns. The character of the relative motion of the ball is illustrated by the projections of the ball trace on the spherical notch on the plane XOY' (Fig. 2), XOZ' (Fig. 3) and Y’OZ’ (Fig. 4). A numerical experiment showed that there is a curve on the surface of the sphere located above the initial position of the ball above which its movements are not carried out (for the parameters of controlled displacements of a supporting body with a spherical recess chosen in the work). This conclusion also follows from the existence condition for the energy conservation integral (39).

For the dynamical system under study with the initial data chosen above, the angular velocity of rotation ro_n of the sphere around the normal n practically all the time during the motion of the ball is zero. Therefore, that part of the kinetic energy of the ball, which corresponds to its rotational component ( to ² = to n + to 2 ), is almost completely concentrated in the energy of pure rolling of the ball with angular velocity to_T .

IN             IN             IN

where    FX =— m • xO; FY =— m • yO; FZ =— m • zO — inertial forces that arise during the translational motion of the spherical recess in space and act on the ball along the axes, OX , OY и OZ , respectively.

In the integral (39), the terms with negative signs correspond to the portable component of the motion of the heavy ball in the movable notch.

• V.    Results of Numerical Experiment

Integration of the resulting system of differential equations (33) - (35) and the study of the dynamic behavior of a nonholonomic mechanical system were carried out numerically using the certificated "MATHCAD" software. In this case, the translational motion of the vertex of the spherical recess was given by the following three periodic functions of time in accordance with normative documents [2, 3]:

xO (t ) = A • e-^1^t • sin (to • t);

yO (t) = B • e~^2^t • sin(to2 • t);

zO (t) = C• e”^3^t • sin(to3 • t) .

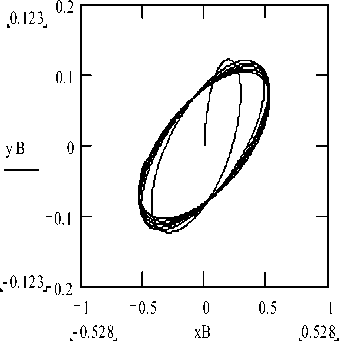
Fig.2. Projections of the ball trace on the spherical groove on the plane X’O’Y*

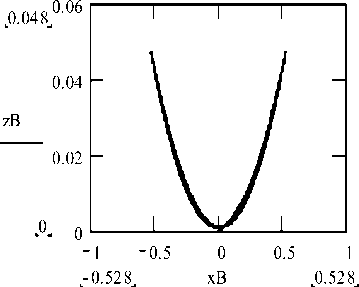
Fig.3. Projections of the ball trace on the spherical groove on the plane

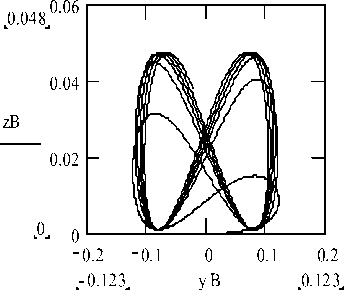
Fig.4. Projections of the ball trace on the spherical groove on the plane Y ′ O ′ Z ′

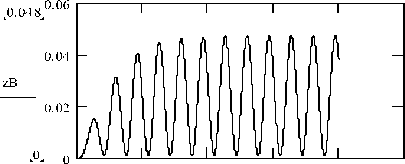
Figure 5 shows the time variation t of the angular velocity of the pure rolling of the ball ωτ in rad / s. For comparison, Figure 6 shows the evolution of the zB (m) applicator of the ball trace in time t in the movable axes O ′ X ′ Y ′ Z ′

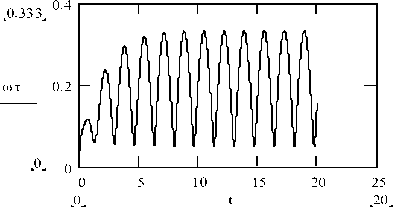
Fig.5. Time variation t of the angular velocity of the pure rolling of the ball ωτ in rad / s

0        5        10        15       20        25

0                           t                         20

Fig.6. The evolution of the zB (m) applicator of the ball trace in time t in the movable axes O ′ X ′ Y ′ Z ′

• VI.    Conclusions

In this paper we construct a mathematical model for the dynamic behavior of a heavy homogeneous ball in a moving spherical recess that performs a given translational motion in space. In this case, the ball rolls in the recess without slipping. The kinematic and dynamic equations of motion of the "heavy ball – mobile spherical recess" system are derived using the nonholonomic mechanics of Appel. In this problem, the energy conservation integral was obtained. On the basis of the obtained differential equations, a numerical analysis of the evolution of the ball motion in a movable recess was carried out.

A numerical experiment has shown that on the surface of a moving sphere there exists a curve located above the initial position of the ball above which its movements are not realized. This conclusion also follows from the condition for the existence of an integral of conservation of energy in a given problem. In addition, if the initial data is chosen so that the angular velocity of rotation ω of the ball around the normal n is zero, it remains practically zero throughout the ball's motion. This is explained by the fact that that part of the kinetic energy of the ball, which corresponds to its rotational component ω ² = ω _n ² + ω_τ ² , is completely concentrated in the energy of the pure rolling of the ball with angular velocity ω_τ .

• [1]    Den Hartog J.P. Mechanical Vibrations. McGraw-Hill, New York, 1956. – 436 p.

• [2]    Dynamic calculation of buildings and structures: Handbook of the designer (in Russian) / Ed. B.G. Korenev, I.M. Rabinovich. – Moscow: Stroiizdat, 1984. – 304 p.

• [3]    Dynamic calculation of special engineering buildings and structures: Handbook of the designer (in Russian) / Ed. B.G. Korenev, A.F. Smirnov. – M.: Stroiizdat, 1986. – 185 p.

• [4]    N.A.Fufaev. A sphere rolling on a horizontal rotating plane // Journal of Applied Mathematics and Mechanics, 1983, V.47, Issue 1, p.p. 27 – 29.

• [5]    N.A.Fufaev. Theory of the motion of systems with rolling // Journal of Applied Mathematics and Mechanics, 1985, V.49, Issue 1, p.p. 49 – 53.

• [6]    N.A.Fufaev. Rolling of a heavy homogeneous ball over a rough sphere rotating around a vertical axis // Soviet Applied Mechanics, 1987, V.23, Issue 1, p.p. 86 – 89.

• [7]    Korenev B.G., Reznikov L.M. Dynamic Vibration Absorbers – Theory and Technical Applications. Chichester. – John Willey and Sons‖. – 1993. – 296 p.

• [8]    Legeza V.P. Vibration protection of dynamic systems with roller absorbers (in Ukrainian). – Kyiv, "The Fourth Wave", 2010. – 280 p.

• [9]    Legeza V.P. Numerical analysis of the motion of a ball in an ellipsoidal cavity with a moving upper bearing // Soviet Applied Mechanics. – 1987. – Vol. 23, №2. – P. 191 – 195.

• [10]    Legeza V.P. Kinematics and dynamics of a mechanical system on rollers that provide nonholonomic constraints // Journal of Mathematical Sciences (Kluwer Academic Publishers–Plenum Publishers). –1994. – Vol. 72, №5. – P. 3299 – 3305.

• [11]    Legeza V.P. Plane problem on a heavy ball rolling in a spherical recess of an inverted pendulum // Int. Appl. Mech. – 2001. – Vol. 37, №8. – P. 1089 – 1093.

• [12]    Li J., Zhang Z., Chen J. Experimental Study on Vibration Control of Offshore Wind Turbines Using a Ball Vibration Absorber // J. Energy and Power Engineering, 2012, № 4. – P. 153 – 157.

• [13]    Lobas L.G. On Rolling Systems // Int. Appl. Mech. – 2000. – 36, № 5. – P. 691 – 696.

• [14]    Lurie A.I. Analytical mechanics. – Berlin: Springer – Verlag, 2002. – 864 p.

• [15]    Neimark Yu.I., Fufayev N.A. Dynamics of nonholonomic systems. – Providence: Amer. Mathem. Society, 2004. – 518 p.

• [16]    Obradovic A., Savinic S., Radulovic R. The brachistochronic motion of a vertical disk rolling on a horizontal plane without slip // Theoretical and applied mechanics, V. 44 (2017), Issue 2, p.p. 237 – 254.

• [17]    Pirner M. Actual Behaviour of a Ball Vibration Absorber // Wind Engineering and Industrial Aerodynamics. – 2002, Vol. 90, №8. – P. 987 – 1005.

• [18]    Pirner M., Fischer O. One prototype of the ball absorber and its effect on the tower // Int. Association for Shell and Spatial Struct. Proc. Working Group IV Masts and Towers. 19th Meeting in Krakow, Poland, September, 1999. – P. 187–196.

• [19]    Pirner M., Fischer O. The development of a ball vibration absorber for the use on towers // IASS, Jour. Of the Int. Association for shell and spatial structures, 2000, Vol. 41, №2. – P. 91 – 99.

• [20]    Weaver W., Timoshenko S.P., Young D.H. Vibration Problems in Engineering, 5th Edition. – John Wiley (N.Y.), 1990. – 624 p.

• [21]    Zhang Z. –L., Chen J.–B., Li J. Theoretical study and experimental verification of vibration control of offshore wind turbines by a ball vibration absorber // Structure and Infrastructure Engineering, Taylor & Francis, 2014, Vol. 10, № 8. – P. 1087 – 1100.

• [22]    Zhang Z. –L., Li J., Nielsen S.R.K., Basu B. Mitigation of edgewise vibrations in wind turbine blades by means of roller dampers // J. of Sound and Vibration, 333 (2014). – P. 5283 – 5298.

• [23]    Zhengbing Hu, Viktor Legeza, Ivan Dychka, Dmytro Legeza. Mathematical Model of the Damping Process in a One System with a Ball Vibration Absorber // International Journal of Intelligent Systems and Applications (IJISA), Vol. 10, No. 1, Jan. 2018, p.p. 24 – 33.

  
  
  

Ivan Dychka: D.Sc., Prof., is a Dean of Applied Mathematics, National Technical University of Ukraine ― Igor Sikorsky Kyiv Polytechnic Institute, Ukraine. His research interests are Computer systems and networks software, automated control systems, Intelligence and expert systems,

Databases and knowledge bases, Information security software for computer systems and networks.

Ruslan Hadyniak is a teaching assistant at Applied Mathematics of National Technical University of Ukraine ― Igor Sikorsky Kyiv Polytechnic Institute, Ukraine. Main science interests are distributed software architecture, data and processes modelling, natural language processing.

Lіubov Oleshchenko is a Candidate of Science (Engineering), Senior Lecturer of Department of Computer Systems Software of National Technical University of Ukraine ― Igor Sikorsky Kyiv Polytechnic Institute, Ukraine. She graduated from the Faculty of Physics and Mathematics of Taras Shevchenko Chernihiv Pedagogical

University, specializing in «Mathematics and Computer Science». She is author and co-author of over 30 scientific works. The results of scientific research are protected by 10 copyright certificates. Areas of major scientific interest: gravitational model and information technology in transport systems, mathematical modeling, computer networks, mathematical programming.