Mathematical modeling of physical and chemical processes in porous media in solving the problems of nanocomposite materials and water-filling

Original article

The concept of «porous medium» (PM) usually corresponds to a certain volume of space, in which there are both solid substance, usually called the matrix or solid phase, and voids – pores filled with air, gas or liquid of different nature. The main characteristics of PM are its porosity – the ratio of the pore volume to the total volume of the area and the reaction surface – the area of the solid phase in a unit volume of the porous medium. When solving scientific and technological problems that involve the study of processes in porous media, both the properties of the porous materials that compose them and the mechanisms of physical and chemical homogeneous reactions in the volume and heterogeneous ones at the phase interface are used.

In most cases, to solve various scientific, materials science, technological and engineering problems, experimen-

CONSTRUCTION MATERIAL SCIENCE tal studies of the macrokinetics of processes and the development of scientific and technological recommendations for the use of processes in porous materials are required. However, the complexity and labor intensity of systematic experimental studies of processes in PS determine the need for modeling, in particular, mathematical modeling of physical and chemical reactions in porous materials. Mathematical modeling makes it possible not only to identify and study the determining physical and chemical processes in the pores and on the solid phase of the porous medium, but also to solve the problems of optimization and optimal process control by selecting the most favorable conditions and modes of solving technological problems.

The aim of the work is mathematical modeling of processes: 1) creation of composite and nanocomposite materials; 2) moisture absorption in porous materials; 3) moistening of porous materials.

To create composite materials in various industries (aviation, space, engineering, medical, chemical, etc.) carbon fiber materials (CFM) are widely used, representing a volumetric-porous medium with different technological properties. Usage of CFM for the above tasks is connected with deposition of metals, alloys or their compounds on the surface of their constituent fibers. One of the promising methods for this is electrochemical, which allows controlling current and hydrodynamic regimes of electrolysis, electrolyte composition and design of the electrode system. At the same time the problem of uniform deposition of metal or CFM coating by metal with certain profile along the material thickness is solved. Obviously, an effective solution is to use methods of mathematical modeling and optimization of metal deposition processes in a flow-through threedimensional electrode (FTE) based on CFM.

The problems of moisture absorption and moistening of porous materials arise in the implementation of various technological processes in materials science, industrial and construction ecology. As in the previous case, effective methods for calculating optimal conditions of physical-chemical processes of moisture-moisture absorption are methods of mathematical modeling of processes in porous media, based on physical-chemical theory of porous media, modern numerical methods and computational technologies.

The task of mathematical modeling of relative humidity distribution of conditioned air in porous media, in particular in the volume of compactly formed textile semifinished products, is actual both for development of theoretical positions and for improvement of technological processes of moisture absorption-moistening of materials. Significance of solution of scientific and technological problems of dampening-damping of various materials is determined by the necessity of improvement of physical and mechanical properties of dampened fibers, such as tensibility, elasticity, etc. As it is noted in literary sources, research of moisture absorption-wetting processes, including by methods of mathematical modeling, promotes development of theoretical positions and allows to determine technological parameters providing the greatest efficiency of process [1–7].

METHODS AND MATERIALS

Mathematical models of physical and chemical processes in volumetric-porous pseudo-homogeneous media

When building mathematical models of processes in PS, we will use the idea of Academician B.Y. Zel’dovich [8], when a porous medium is represented as a pseudo-homogeneous one, in each elementary volume of which a kinetic reaction corresponding to a certain physical and chemical process takes place. Naturally, kinetic and other parameters, such as diffusion coefficient, adsorption rate constant, specific reaction surface, porosity coefficient, etc., should have some averaged values under this approach. At the same time, on the basis of theoretical ideas about the description of electrode, diffusion and hydrodynamic processes in porous media, we will give mathematical statements in the form of boundary value problems for systems of differential equations and methods of their solutions for specific technological problems.

Electrochemical metallization of carbon-graphite fibrous materials.

When creating composite and nanocomposite materials based on CFM, it is necessary to organize the process of electrochemical coating of the solid phase – porous material, ensuring uniform deposition on the carbon-graphite filaments that make up the FTE, or deposition of a certain profile along the electrode thickness. To determine the most favorable electrodeposition conditions, the use of mathematical modeling makes it possible to set and solve the optimization and optimal control of the metallization process [9].

In most electrochemical systems, the theoretical laws of migration and convection of charged particles described by systems of partial differential equations are realized [10, 11]:

^ = -WiUiFC^E + C,v) ,        (1)

where z _i , C _i , u _i are the charge, concentration and mobility of the i -th electroactive component in the pseudo-homogeneous medium; 7 E is the gradient of the electric field potential; v is the vector of the convective solution transfer rate; t – current process time; F – Faraday number, 7 • – vector divergence.

The system of differential equations (1) can be transformed taking into account pseudo-homogeneity of the medium, when in each point of the electrode space there is a reaction of metal ion deposition on the solid phase of

CONSTRUCTION MATERIAL SCIENCE the medium and, as a result, there is no electro-neutrality of the solution, which is inherent to homogeneous electrochemical systems in the absence of reactions in the electrolyte volume. This entails the inequality to zero of the derivatives of the concentrations of electroactive substances (metal ions that precipitate) at any point with coordinate x along the FTE thickness, ∂Ci /∂x ≠ 0. Let us also consider that for most CFM metallization problems it is sufficient to consider an electrolyte with one component, the coating metal, i = 1, and the case where the metallization process can be modeled by a one-dimensional stationary differential equation, assuming that the same electrochemical processes occur in all sections of the FTE horizontal and vertical planes, and that the dependence of metal concentration in the FTE volume on time changes slowly during deposition and, in first approximation, these changes can be neglected. Under such conditions, in accordance with the rules for constructing mathematical models of processes in FTE described, for example, in [12], eventually, the differential relation (1) can be transformed to the following system of ordinary differential and algebraic equations:

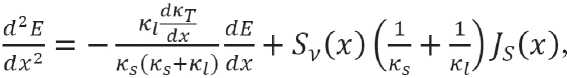
dC dx

—JsM

vzFJ5V '

with boundary conditions:

C(O) = C„, ^(0)=^/, Ц(Ц = ^/, (4) v л               v

JM=j0

ехр(а₂Р((Е-ф_к)/КТ)-ехр((а-1)₂Р(Е-ф_к)/НТ) l+;₀ ехр(а2Р(Е-ф_к)/НТ)/2РК_17гС

, (5)

problem of optimal control of metallization of the CFM. This is due, firstly, to the significant influence of S _v value on the resulting process parameters, such as the uniformity of deposit distribution, or the total amount of deposited metal and, secondly, to the possibility of ensuring the necessary specific surface area of FTE in different vertical sections of the electrode due to artificial compressionexpansion of the cathode material (CFM) [9]. With this approach, the problem (2)-(5) can be transformed to the form necessary for realization of L.S. Pontryagin’s maximum principle [12, 13], application of which allows to calculate the most effective, according to the given uniformity criterion, distribution S _v ( x ).

Moistening of a porous material with moist air.

When building a mathematical model of the process of humidification of porous material by conditioned air flow, taking into account the assumptions accepted earlier, we will assume that in each elementary volume of porous space, taken as a point in the volume of medium, there is a reaction of moisture adsorption, which has its microscopic regularities.

Obviously, the most important driving forces of wet air penetration to the internal, hard-to-reach areas of the porous material are the forced air flow and the diffusion mechanism. In this case, consideration of the microscopic reaction rate of moistening of the medium should be made in accordance with the theory and practice of dependence of moisture content of the material on the relative air humidity and thermal conductivity of the medium.

Based on the law of conservation of matter, in each point of the considered medium, the change of humidity ϕ in time t obeys the equation [14]:

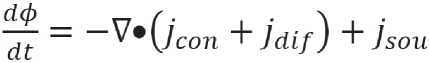
where J – the overall current density fed to the FTE, C ₀ – metal concentration at the electrode inlet, κ _s , κ _l – the exchange current density, j ₀ , α, φ _R – respectively, exchange current density, transfer coefficient and equilibrium potential of the electrochemical reaction; R – universal gas constant; T – absolute process temperature; K _m – mass transfer coefficient.

Depending on the selected modes of deposition of metallic sludge on CFM, some electrochemical parameters of the process and the system can be dependent on both the process time and the coordinate on the thickness of the electrode. These are such values as the specific electrical conductivity of the solid phase of the system – CFM, the specific reaction surface and the porosity factor of the electrode material. Calculation methods for the above dynamic parameters were developed by us and published, for example, in the monograph [11].

Note that the specific reaction surface, considered as a function of the electrode thickness coordinate S _v = S _v ( x ), can be selected as the controlling action when setting the

Here j _con = ϕ • W is the forced air flow conditioned by the presence of the initial velocity of air supply into the PM; w = ( w ₁ , w ₂ , w ₃ ) – vector of velocity of conditioned air through the PM; j _dif = D V ( ϕ ) – the flow due to moisture diffusion; D – averaged diffusion coefficient; j _sou = kF _S f ( ϕ ) – negative source caused by moisture loss from humidifying air due to moisture adsorption in each point of the pseudo-homogeneous medium volume; k – adsorption rate constant per unit surface; F _S – specific surface per unit volume of PM.

The source density of moisture absorption from humidifying air f ( ϕ ) obviously depends on the mechanism of material moistening and is determined by the form of moisture bonding with a moist material [7, 14]. Many models exist to describe such a mechanism, for example [3], which, however, describe particular physical and chemical processes and are inconvenient in mathematical modeling. We have developed an original approach to the description of the moisture adsorption curve in the form of a functional dependence f ( ϕ ), presented below.

CONSTRUCTION MATERIAL SCIENCE

Modeling of the moisture adsorption curve.

The adsorption curve in this case represents the dependence of the equilibrium moisture content W ( x ) in any point of pseudohomogeneous medium on the relative air humidity ϕ ( x ). Experimentally obtained adsorption curves are shown in Fig. 1.

The analysis of the curves presented in Fig. 1 makes it possible to identify two sections for the description of the experimental dependence by the analytical function: at 0 <  ϕ ( x ) <  ϕ _c (60–70%) – the section convex downward, and at ϕ _c <  ϕ ( x ) < 100% – the section convex upward; ϕ _c is a certain averaged constant that has a certain value for each type of porous material. At each of the selected sections, let us establish an analytical dependence of the equilibrium moisture content on the air flow humidity W = ϕ ( x ) and use the following reasoning.

In the first segment of the curve, the growth rate of adsorbed moisture volume is proportional both to its value at a given moisture content W and to the difference (WM–W), where WM is the limiting moisture content of the porous material. This is conditioned by the fact that, first, precipitated moisture molecules create additional adsorption centers which promotes acceleration of moistening, and second, by possibility of growth of W up to the point of WM saturation. The result of the above reasoning is the equation dW/dϕ = kW(WM–W), where k is a coefficient of proportionality.

Knowing the initial equilibrium moisture content of fibers W _n , it is not difficult to obtain the solution of this equation:

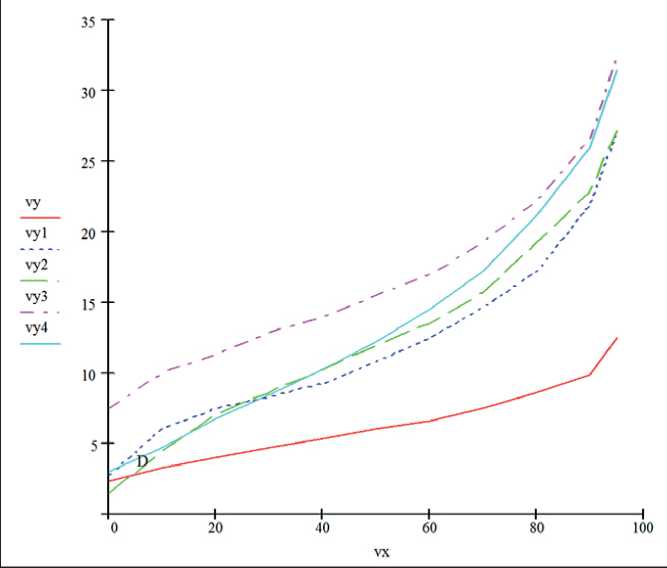
Fig. 1. Dependence of equilibrium moisture content of fibers W = ϕ ( x ): vy4 – viscose, y3 – yarn, vy2 – wool, vy1 – roving, vy – kapron

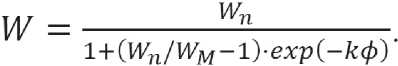
In the second section at ϕ ≥ ϕ _c the mechanism of moisture filling of the capillary-porous medium has a monomolecular and then a capillary character [13], which determines the exponential growth of W with increasing ϕ :

W = k ₂ • exp ( k ₁ ( ϕ – ϕ _c )),

where k1, k2 and ϕc are some effective parameters whose value can be determined by the method of least squares for each specific porous material. Combining curves (9) and (10) leads to a description of the dependence of W on ϕ as an algebraic function w = k2 ехр(к^ф - 0J) + 7—7-77^77——- (9)

.()

The theoretical and experimental curves corresponding to the data in Fig. 1 are shown in Fig. 2.

Parameters of curves (11), calculated by the method of least squares, are given in table 1.

Mathematical model of moisture distribution in the volume of porous medium.

Equation (6), taking into account representations (7), (8), in the expanded form looks as follows:

dt V¹ dx ^W2 dy^Ws dz) \dx² dy² dz²) s/(0). (10)

Let us also assume that the flow of conditioned air through the porous medium boundary allows us to simplify equation (10) to one-dimensional. This is possible, for example, when the lines of air flow through the flat boundary of the porous medium are parallel or when equation (10) can be written in cylindrical or spherical coordinates, which is often realized in real humidification technologies. The assumptions made do not limit the generality of the mathematical model, but allow avoiding cumbersome transformations when describing the solution of the problem.

Within the framework of the accepted assumptions, equation (10) is transformed to the form:

йф        йф ,dw _г.с1²ф , _r ,_v ,-x _/11X

"^⁼"^W^" Ф^"⁰^^^^^ . (11)

The initial condition for problem (10) is obvious:

ϕ (0, x ) = ϕ ₀ .

It is also obvious that at the point x = 0 (at the border of the porous medium – surface), through which humidification is carried out, the humidity corresponds to the humidity of conditioned air supplied to the technological zone – ϕ ₁ :

CONSTRUCTION MATERIAL SCIENCE

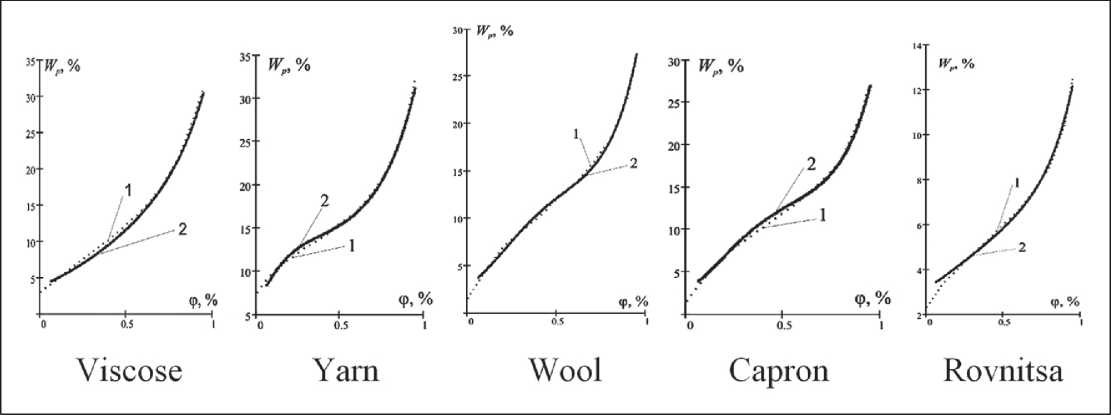
Fig. 2. Adsorption curves: 1 – experimental, 2 – calculated

Table 1

Type of material	W n	W	k 2	k 1	k	ϕ c	S 2
Viscose	14.9	3.5	3	4.4	3.3	0.55	2.5
Yarn	13	6	3	4.5	10	0.55	1.8
Wool	13	2.7	2	6.6	6.5	0.65	1.9
Rovnitsa	13	2.7	2	6.5	7	0.65	2.4
Capron	8.5	31	0.9	5.95	23	0.66	0.84

ϕ ( t ,0) = ϕ ₁ . (13)

To solve problems (11)–(13) it is necessary to know the boundary condition for the derivative dϕ (0)/ dx at x = 0. Let us isolate an elementary volume in a porous medium of unit cross-sectional area and small thickness V _m and consider the change in the moisture content of air as it passes through a porous medium of a given volume.

The relative humidity of air ϕ ( x ) in this volume will change as it moves through the medium. Thus, after passing through the thickness of the medium for a distance ∆ _x the air humidity will change to Φ _∆ due to moisture sorption, hence

ϕ0–ϕ∆ = (Qp0–Qp∆)/Qmax, where Qp0,Qp∆ are amount of water vapor in a unit volume of moist air, respectively, before and after moistening the volume Vm of the PM; Qmax – the maximum amount of water vapor per unit volume of moist air. Consequently, the value Vmax (ϕ0–ϕ∆ )•Vm/Ve is equal to the amount of moisture adsorbed in the pores of the medium volume Vm (Ve – unit volume).

At each point of the porous medium the moisture is deposited according to the law of adsorption, i.e. the adsorption curve, which depends on the physical and chemical characteristics of the medium: W(x) = f(ϕ(x)), where W(x) is the specific moisture content of the solid component of the PM at point х. Then the amount of adsorbed moisture in the volume Vm of the medium will be ρSm ∫0∆x(f(ϕ(x))–W0)dx, where Sm – is the area occupied by the solid phase, ρ is the density of the PM, W0 is the specific moisture content of the material before wetting. Thus, we obtain:

Q max ( ϕ 0 – ϕ ∆ )•( V m / V e ) = ρS m ∫ 0 ^{∆ x} ( f ( ϕ ( x ))– W 0 ) dx .

Let’s divide both parts of this equality by ∆ _x and pass to the limit at ∆ _x → 0. In this case it is logical to assume that after the limit transition the area V _m will represent a part of the unit surface S _m corresponding to the pore area, i.e. ε • S _e , where ε is the porosity coefficient. Respectively, S _m is a part of the unit surface occupied by the solid phase of the medium, i.e. S _m = (1– ε )• S _e . We obtain the condition for the derivative function ϕ ( x ) at х = 0:

^^^-^.^(^(o))- ^₀). (14) c Vmax

Thus, mathematical model of humidification of porous material at influence of humid air blown through it

CONSTRUCTION MATERIAL SCIENCE in general statement represents non-stationary boundary problem for partial derivative equation (10)–(14).

Proceeding from real technological conditions of the considered process of moistening of porous material, it is possible to assume that in a number of cases, dependence of humidity of fibers on time in the thickness of medium can be considered as piecewise constant, since change of moisture absorption conditions occurs slowly enough and, consequently, for large time intervals, the process of moisture distribution in the PM has quasi-stationary character, therefore, in each of such intervals d_ϕ / d_t = 0 and equation (11) is transformed to stationary form:

„ d2ф , dф ,   , dw    ,   „ d.x2   ^ dx ^ dx s f ^Ф^ .   (15)

LLA          1Л.Л

Equation (14) with initial conditions (12), (14) is a Cauchy problem for the ordinary differential equation [15] and can be solved in different ways, for example, by finite-difference ones.

In accordance with representation of fibers humidity dependence on time in the form of piecewise constant function, the whole time interval of process [0, T ] is divided into subintervals by Ti points, and in each of subintervals [ T_i , T_{i +1} ] there are specific values of physical parameters of PM, which correction is necessary for each next subinterval because of material properties change as a result of moisture deposition by medium volume m on solid fibers, their swelling and, consequently, fibers radius increase, which, in its turn, leads to and Using classical expressions for determining the specific reaction surface of the fiber material and its porosity, as well as the measured average fiber radius d and the density of the wetting liquid ρ :

^m pV ’ ^S'^m cl pV(l-e) ’ ^m £_m . (16)

For calculations using equations (12), (13), (15), (16) the Runge-Kutta method with automatic selection of the integration step was used.

Moisture absorption in lime composites.

The penetration of humid air to the internal parts of the porous composite is carried out mainly by the diffusion mechanism. Air movement due to forced or natural convection seems to be less important in this case because of the sufficient density of the material and its porosity, which is less than 50% of the total volume of the material.

The mechanism of the reaction of moisture absorption, as in the case of moistening of porous fiber material, is determined by the moisture adsorption curve, the concrete form of which depends, of course, on the material properties. In this case, the mathematical model of the adsorption curve, the method of modeling and all the conclusions concerning its properties made above are also true for the process under consideration.

Similarly, as it was done for the previous problem, the mathematical description of adsorption patterns of moisture absorption of the curve of dependence of equilibrium moisture content of material W on relative air humidity ϕ is obtained:

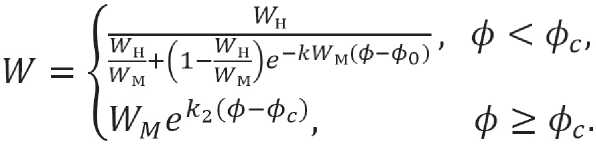
Here W_n – initial value of moisture content; W_M – maximum possible moisture content of the material; k ₁ , k ₂ and ϕ_c – operating parameters, whose value is determined by mathematical processing of experimental curves using the least squares method.

As before, we will assume that the process of moisture absorption, in first approximation, is one-dimensional in spatial coordinates, and we will study its regularities using a one-dimensional mathematical model.

Based on the basic equation of moisture mass transfer in porous media (10), taking into account assumptions and equations made, mathematical description of the process of moisture absorption can be written in the following form

³^^=DS-^ksfw . (18)

Here: D is effective diffusion coefficient; S is specific surface area per unit volume of material; k is some constant; 0 ≤ x ≤ L , L is thickness of porous material.

The solution of equation (18) is obtained using the source function [16], it is assumed that outside the wetted material array x ≤ 0 and x ≥ L , f ( x ) = 0:

. (19)

When the humidification process can be considered stationary, equation (18) is simplified:

D^-kSf^ = 0 . (20)

If the initial air humidity ϕ ≥ ϕc is significant, only the second part of the adsorption curve (convex upward) can be considered kSf(ϕ) = WM e(k2 (ϕ-ϕc)), which allows us to write the equation for calculating the moisture content of the porous medium as

П^-Ш_ме^к2(-^ф-^ф^ =0.          (21)

The solution of the differential equation (21) is not difficult and represents the following system of algebraic expressions:

CONSTRUCTION MATERIAL SCIENCE

^2.1^__1_р-к2(Фь-Фс)-е-к2(Фо-Фс)]

е-кг^Фь-Фс)

Сг =   —

Фь-Фо

_ Фо-Фс [г2 ™м _ _J_ \_е-к₂^ф_ь-Фс) _ _е-кг(Фо-ФсУ Фь-Фо [   20 (k₂yV^{e             6}          .

W_M     cl. W_M

Vw(x)(k₂)2   k₂   И/(Х)

. (22)

.2^

’ 2D '

RESULTS AND DISCUSSION

Metallization of carbon-graphite fibers.

In order to improve the properties of composite and nanocomposite materials created on the basis of CFM, mathematical modeling and optimization of metal deposition processes in FTE were performed.

Verification of the obtained models was based on the experimental studies performed by V.K. Varentsov [17, 18] suggesting modification of surface properties of CFM of a certain grade in order to obtain uniform precipitation during metallization of the material by electrochemical method. Woven, nonwoven, and combined carbon materials differing in specific conductivity, reaction surface, and porosity were used [19–22]. Electrochemical modification of CFMs was carried out in solutions of various electrolytes by anodic polarization or sequentially by cathodic-anodic polarization, or by various combinations thereof. It was shown that as a result of electrochemical treatment, the hydrophilic properties of the material significantly improve, which is due to an increase in the number of surface oxygencontaining groups.

Deposition of metals on pre-treated electrochemical materials allows to calculate the optimal modes of elec- trodeposition, which makes it possible to obtain uniformly distributed metal precipitations over the thickness of the electrode, improve structure, morphology and composition of precipitations, hence, the properties of the composite material (Fig. 3).

As an illustration of efficiency of using mathematical modeling when solving the problems of determining the effective technological regimes of metallization of CFM was chosen the problem of coating CFM brand VVP-66-95 with silver electroplating from sulfuric acid thiourea solution. The results of calculations of metal distribution on FTE thickness by mathematical model (2)–(5) and, for comparison, experimental data of silver distribution are shown in Fig. 4.

As an illustration of the efficiency of using the method of mathematical modeling when solving problems on determining the effective technological regimes of metallization of CFM was selected the task of coating CFM brand VVP-66-95 with silver electroplating precipitate from sulfuric acid thiourea solution with the following parameters of the electrochemical system: electrode thickness – 1 cm; current density – 0.2 A/m ² , solution flow rate – 0.56 cm/sec; specific surface area – 255 cm ² /cm ³ , specific electrical conductivity – 0.03 S/cm, porosity – 0.95; specific electrical conductivity of solution – 0.1 S/cm; electrolysis time – 60 min; composition of electrolyte: H ₂ SO ₄ – 0.5 mol/liter, thiourea – 50 g/liter, silver – 76 mg/liter. Results of calculations of metal distribution on FTE thickness by mathematical model (2)–(5) and, for comparison, experimental data of silver distribution are shown in Fig. 4.

Fig. 3. Microphotographs of copper precipitation on the initial (a) and electrochemically modified (b) CFM

CONSTRUCTION MATERIAL SCIENCE

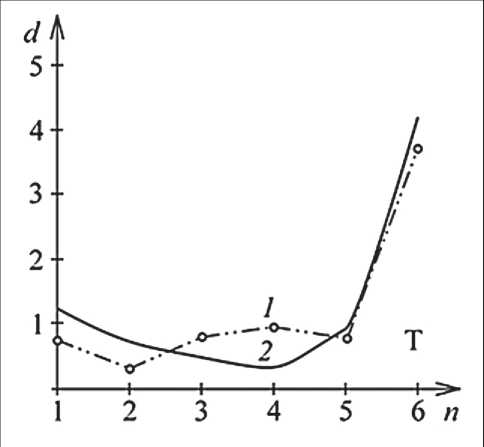
Fig. 4. Distribution of silver deposit by electrode thickness: 1 – experiment, 2 – calculation; d – ratio of metal mass to CFM mass; n – layer number; T – back side of electrode

Let’s emphasize that nanosized particles of metals can be electrolytically deposited on the surface of CFM fibers, which makes it possible to obtain dense coatings of carbon-graphite fibers with a given profile. As an illustration, here are photos of platinum precipitation morphology on carbon-graphite filaments, Fig. 5.

The correspondence of the presented in Fig. 4 experimental and calculated curves of silver distribution over the thickness of the FTE with cathode from the selected FCM confirms the effectiveness of the above mathematical models and calculation algorithms used by us, described above and in our other works, for example [9, 11, 13, etc.]. It is reasonable to conduct numerical experiments to study the processes of metal electrodeposition when creating composite materials with a certain morphology and distribution of metal precipitation on the surface of FCM fibers.

Forced humidification of compactly formed textile fibers.

Representation of a wetted material as a limited PM with basic effective characteristics distributed over its volume allowed to develop a mathematical model in the form of a boundary problem of mathematical physics, which allows calculating the distribution of relative humidity in the porous medium volume during its moistening by a moist air flow.

To illustrate the efficiency of the algorithm, Fig. 6 shows the results of calculating the change of relative humidity in the volume of a PM under the linear law of change in the velocity of humidifying air w ( x ) = γx + µ .

The results of calculations and experimental data show their sufficient correlation. Both from calculations and from experiments, it follows that an increase in the velocity of humidifying air contributes to a more uniform distribution of moisture in the volume of the humidified material. At the same time, it is obvious that increasing the intensity of blowing wet air through a compactly formed textile material requires either increasing the capacity of the ventilation device or increasing the porosity of the material.

Moisture absorption in porous building materials.

Fig. 7 shows calculated (curves) and experimental (points) data of moisture absorption for two porous materials: foamed vermiculite sand (1) and aluminosilicate ash microspheres (2). For the numerical implementation of the mathematical model (22), the following param-

Fig. 5. Microphotographs of platinum sediments on CFM

CONSTRUCTION MATERIAL SCIENCE

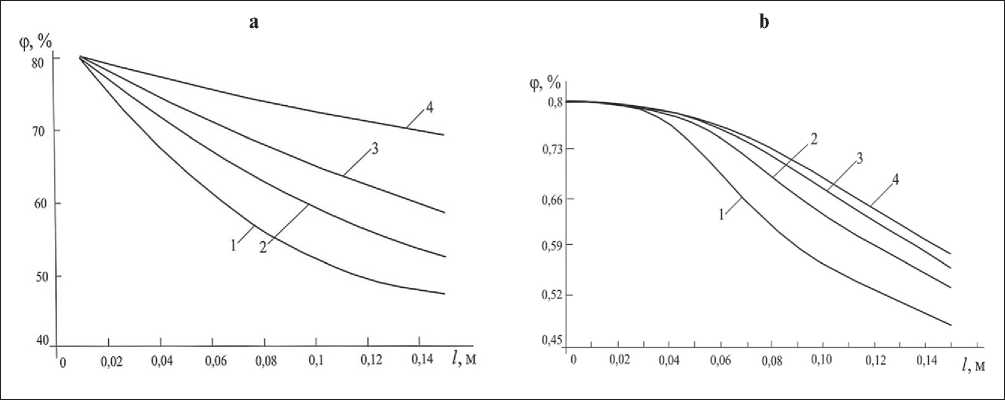
Fig. 6. Effect of initial air flow velocity v on the distribution of relative humidity in the volume of PM, taking into account the linear velocity drop in the volume of the medium: a – calculated, b – experimental curves (1) – (4), respectively, at v = 2, 4, 6, 8 m/s

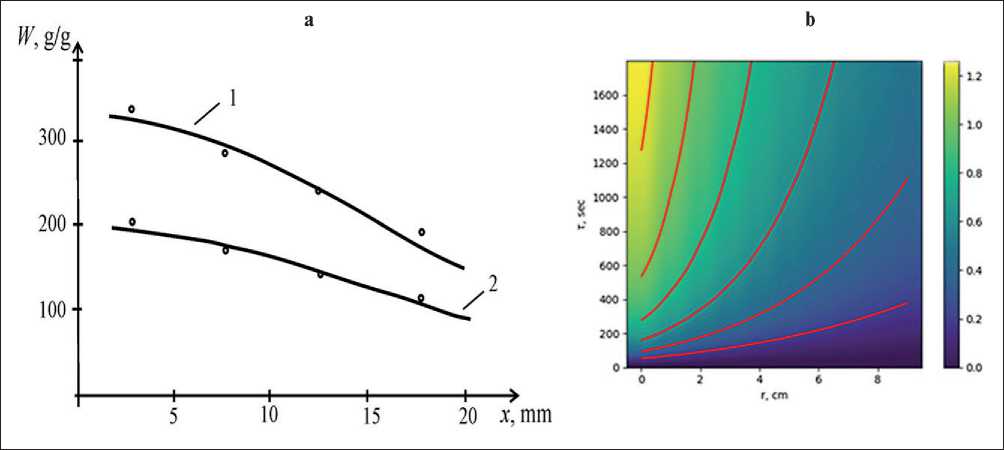
Fig. 7. Distribution of moisture content in the finishing coating: a – calculation in blown vermiculite sand (curve 1), in ash microspheres of aluminosilicate (2); points – experiment; b – moisture distribution in the volume of porous material with the process time.

eter values found from experimental adsorption curves were used: k ₂ = 0.016, L = 2 cm, (0) = 100, ϕ ( L ) = 50 and diffusion coefficients D ₁ = 7.67×10 ^–5 and D ₂ = 3.43×10 ^–5 cm ² /sec for the corresponding curves [23].

The calculated and experimental curves presented in Fig. 7a, show good agreement, and, consequently, the effectiveness of the mathematical model. Fig. 7b allows us to conclude about sufficient difficulties of the process penetration into the material thickness even at significantly long wetting time.

Analyzing the results of calculations, we can conclude that, apparently, the diffusion coefficient value significantly affects the moistening process of a porous material and can be used as a measure of the possible moisture content of the composite.

It should be noted that for the calculations, computer programs were developed using the mathematical environment MathCAD and the Python programming language with the libraries/modules Numpy, Scipy and Matplotlib.

CONSTRUCTION MATERIAL SCIENCE

CONCLUSION

Thus, the research presented in this paper utilizes methods of mathematical modeling of physical and chemical processes in PM based on theoretical ideas about electrode, diffusion, migration, adsorption processes and their distribution in pseudo-homogeneous systems. On the basis of representation of porous material in the form of pseudo-homogeneous medium characterized by averaged physical and technological parameters as well as on the basis of physical and mathematical description of processes in PM mathematical models are constructed and boundary conditions for calculation of physical and chemical processes distribution in the considered porous medium at solution of problems 1) metallization of carbon-graphite material when creating composite and nanocomposite materials on its basis; 2) moistening of fibrous material by a forced flow of conditioned air; 3) moisture absorption by porous building materials.

Some characteristics of PM and kinetic parameters available in description of mathematical models (for example, specific reaction surface, material porosity coefficient) can change during both metallization and moisture absorption-humidification processes of porous material, and both towards increase and towards decrease of their values. Other dynamic characteristics of processes, such as linear velocity of electrolyte or humidifying air through PM, etc., may also change. Necessary correction expressions of technological and kinetic parameters in the process of physical and chemical reactions in PM are given in each case under consideration.

The paper provides a mathematical description of the dependence of the equilibrium moisture content of the porous material of lime composite on the relative humidity of air in the form of adsorption curves of moisture in the studied material; built a mathematical model of the moistening of dry construction mixture on the basis of the representation of some elementary volume of lime composite in the form of volume – porous medium with averaged physical and chemical parameters. A comparison of theoretical and experimental curves is presented, their good correspondence is shown.

The calculations and some analysis of the influence of the main parameters of the processes of metallization of CFM, moistening of compactly formed textile material, and the process of moisture absorption in the lime composite on the distribution of processes in the volume of the PM that constitutes the reaction pseudohomogeneous region have been performed.

The presented mathematical models for the given values of the parameters of the processes involved in the relations determined experimentally or by calculation quite adequately describe regularities of physical and chemical reactions distribution in the considered PM, and can be used for theoretical investigations of regularities, as well as for calculation of optimum values of technological parameters of the processes under consideration.