Матрично-графовая модель процесса деструкции полимерных материалов

DOI:

Масштабы промышленного производства полимеров постоянно растут, что приводит к накоплению их отходов. В результате процессов старения полимерные материалы перестают выполнять свои функции, в результате чего требуется их утилизация, переработка и по возможности повторное использование в промышленном производстве. Одними из способов переработки полимеров для повторного использования являются процессы их деструкции различными методами (механическая, термическая, химическая, радиационная и их комбинации) [1].

Механизм деструкции полимеров представляет собой последовательность случайных событий (элементарных актов деструкции) с конечным количеством исходов, которые можно рассматривать как в дискретные моменты времени, так и непрерывно. При этом вероятность перехода в новое состояние (молекулярно-массовое распределение (ММР) полимера) зависит только от состояния, из которого совершается переход и не зависит от всей предыстории процесса. Для описания такого рода процессов может использоваться математический аппарат теории цепей Маркова [2, 3].

Математическая формализация таких процессов включает графические изображения состояний и переходов в виде нагруженных ориентированных графов (рисунок 1), на основе которых составляются системы уравнений Колмогорова-Чепмена [4]. Ввиду большого количества состояний, определяемого числом фракций и описываемых функцией ММР, а также общности процессов деструкции полимеров, актуальна задача разработки общей матрично-графовой модели, описывающей основные закономерности процесса.

Методика

Основные положения модели: случайная переменная Pi(t) характеризует долю макромолекул длины, соответствующей i фракции ММР в момент времени t. Вероятностный смысл – отношение количества макромолекул в данной фракции (благоприятных исходов) к их общему числу. Под действием агента деструкции с течением времени система макромолекул может переходить из одного состояния в другое. Дискретное конечное множество состояний в соответствии с принятой шкалой описывается множеством состояний в виде следующего множества S = {S1,s2,...,sn},n € 0 , где sn - числовой диапазон длин (масс) макромолекул в i-ой фракции. В рамках теории цепей Маркова приняты следующие допущения: процесс деструкции носит последовательный характер; интенсивность перехода из одного состояния в другое отражает интенсивность процесса деструкции и характеризуется величинойλi,j, а интенсивности обратных переходов равны нулю; процесс деструкции моделируется переходом из состояния XI в xj, где j >i, при этом интенсивностью переходов λj,i пренебрегаем; состояние системы характеризуется вероятностью Pi, где i = 1, N, где N - количество фракций. При принятых допущениях граф Г состояний представлен на рисунке 1. Распределение макромолекул по фракциям соответствует индексам (пусть i =1 фракция с наибольшей молекулярной массой или длиной).

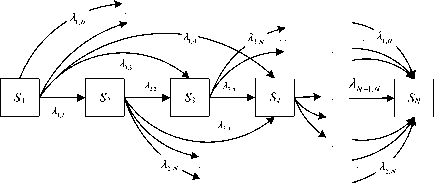
Рисунок 1. Граф состояний процесса деструкции полимеров

Figure 1. Graph of states of the process of destruction of polymers

Обозначим множество вершин V = { v 1 , v 2 ,..., v_N } , а множество дуг D = { d 1 , d 2 ,..., d_K } , где N - число вершин, K – число дуг.

Первой задачей для синтеза матрично графовой модели процесса деструкции является нахождение числа дуг. Для этого сначала рассчитаем число дуг K по заданному числу вершин и структуре графа в виде Г. Рассчитаем число дуг для 2 -x узлов (рисунок 2) .

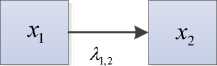
Рисунок 2. Граф, состоящий из двух вершин

Figure 2.Graph consisting of 2 n о d е s

Для графа (рисуно к 2) имеем количество дуг K 2 =2 – 1 =1 , через число вершин N(V) =2, K 2 =N-1.

Для графа из 3 -x вершин к имеющемуся количеству дуг, равному 1, добавится число дуг, равное 3 за вычетом уже имеющейся дуги (рисунок 3) .

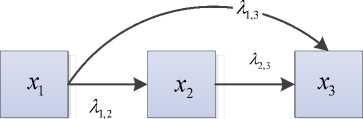
Рисунок 3. Граф, состоящий из 3 -x вершин

Figure 3. Graph consisting of 3 n о d е s

Имеющееся число дуг представим через количество вершин как N -2, а добавляющееся как N -1. Так, для N ( V ) = 3, K 3 =1+ 2 = 3, через число вершин K 3 =( N -1) +( N -2) = (3 – 2) +(3 – 1) = 3.

Тогда, добавляя каждый раз к имеющемуся числу дуг по ( N- ( N -1)), получим для N вершин N -1 слагаемых вида:

K N = ( N - 1 ) + ( N - 2 ) + ... ₊ [ N - ( N - 1 ) ] (1)

^B ( ^ГN ) =

Г 0

Г- 1

- 1 - 1 ... - 1

- 1 1

Представляя выражение (1) как сумму арифметической прогрессии первых ( N -1) членов с первым членом а n = 1 и разностью d =1, запишем:

- 1

- 1

- 1

.01 J , (4) 0 1 Г 0 ' - 1         0

0 ... 0

= ¹ + ( N - 1 ) ₍ N - 1 ) = N ( N - 1 )

Проверим методом математической индукции, что формула (2) для расчета количества дуг для N вершинного графа типа Г верна:

N ( N - 1 ) 2 ( 2 - 1 )

• 1)    K 2 = — ----- = —---- = 1, истинно,

N ( N - 1 ) 3 ( 3 - 1 )

• 2)    K з = — ----- = —---- = 3, истинно,

N ( N - 1 ) 4 ( 4 - 1 )

• 3)    K 4 = ——- = ——- = 6, истинно

(проверяется непосредственно по графу), следовательно, формула (2) справедлива для всех натуральных N >  2 .

Следующей задачей ввиду громоздкости графического изображения графа Г является его кодирование матрицами смежности и инцидентности.

Матрица смежности для графа Г N имеет

размер N • N и принимает вид:
	r 0	1	1 ...	1	1 1
	0	0	1 ...	1	1
A ( Г n ) =	0 ...	0 ...	0... ......	1 ...	1 ...
	0	0	0 ...	0	1
	. 0	0	0...	0	0 ?

при этом генератор матрицы задается системой

a ^{( Г}N ) =

.

Матрицу инцидентности зададим конкатенацией подматриц, соответствующих дугам, исходящим из каждой i -ой вершины, при этом количество подматриц N -1, число строк N , число столбцов матрицы равно числу дуг K , а i -ой подматрицы K-l , где l =1… N :

0 ... 1

0 ... 0

1 J

- 1

где операция © подразумевает конкатенацию

матриц.

Тогда генератор каждой подматрицы для i -ой вершины с соответствующим числом исходящих дуг K-l:

- 1, V i = K - 1

b j ^{- 1 ]} =k V ( i = j л i >  K - l ) ,

0, V ( i ^ l л i ^ j )

i = 1... N , j = 1... K - 1

При наличии обратных переходов, отражающих явления структурирования или полимеризации, возникающие одновременно с основным процессом деструкции, матрицы видоизменяются с учетом новых переходов. Например, для графа, представленного на рисунке 4 матрицы смежности и инцидентности примут вид:

r 0 1

A ( Г ) = 0 0

. 0 1

1 1            r-'

1 B ( Г ) = 1

0 1

- 1   1

,

1 J

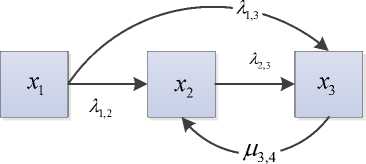
Рисунок 4. Граф с обратными переходами

Figure 4. Graph with backward trаnsitiоns

Для учета интенсивности переходов λ i,j используется нагруженный граф и соответствующие матрицы смежности и инцидентности. Например, для графа, представленного на рисунке 4, матрицы примут вид:

( ⁰   Л ,2

A ( Г ) = 0   0

^ ,3

(- 1

- 1 0

(0 ,/

^ 2,3

0 J

^, B ( Г ) =

0 - 1

0 "

- 1 J

Таким образом, матрицы смежности и инцидентности задают структуру нагруженного графа, описывающего процесс деструкции полимера. Рассмотрим пример синтеза матричнографовой модели для процесса деструкции полибутадиена в растворе. В качестве исходных данных для оценки ММР полимера использовались данные ГПХ раствора полибутадиена. Из исходной

хроматограммы, содержащей 100 фракций усреднением выделено 6 фракций. Определение молекулярных параметров и молекулярно-массового распределения образцов каучука осуществлялись с помощью ГПХ. В качестве оборудования для ГПХ анализа применялась система Breeze фирмы Waters. Результаты экспериментальных исследований представлены в таблиц е 1. Ввиду наибольшей интенсивности процесса деструкции в первый час и необходимости идентификации всех 6-ти фракций ММР разбиение на фракции в ходе процесса деструкции отличается от исходного.

Таблица 1.

Результаты экспериментальных исследований

Table1.

Results of experimental studies

№ фракции	масса M (ln М)	доля фракции при t , ч	масса М (lnM)	доля фракции при t , ч
		0		2	3	4	5
P 6,0	6–7.7	0	31000 (10.34)	0.667	0.887	0.98	0.992
P 5,0	7.7–9.3	0,01	93000 (11.44)	0.234	0.097	0.02	0.007
P 3,0	9.3–11	0.255	155000(11.95)	0.058	0.016	0	0
P 4,0	11–12.7	0,62	217000(12.3)	0.02	0	0	0
P 2,0	12.7–14.3	0.39	279000(12.54)	0.011	0	0	0
P 1,0	14.3–16	0.01	341000(12.74)	0.01	0	0	0

Для заданных условий число вершин

( 0

1 A

графа N = 6, число дуг K рассчитаем через число

вершин по формуле (2) как K =

6 ( 6 - 1 )

= 15.

Матрица смежности для скрытой части графа

A ( Г ) =

.

Г 6 имеет размер 6×6 и в соответствии с генера-

тором (3) примет вид:

Соответствующая матрица инцидентности примет вид:

(- 1

-

-

-

-

1 A

( 0

( 0

-

-

-

-

0 J

( 0

B ( Г ) =

\

-

-

-

Ф

-

j

\

-

Используя полученные матрицы,

-

-

-

описы-

вающие структуру графа, синтезируем матема-

тическую модель в виде графа (рисунок 5) и

матричного уравнения Колмогорова-Чепмена

Ф

-

-

-

j

\

j

-

где

-

-

-

-

-

-

\

-

j

-

d P = Л ■ P ,P| dt             ¹=⁰

.

-

\

j

= P 0 ^,

—

Z A

j = i + 1

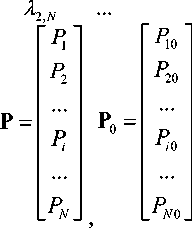
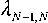
при этом интенсивности потоков Ai,j постоянны, вектор P0 задает начальное ММР полимера до начала процесса деструкции.

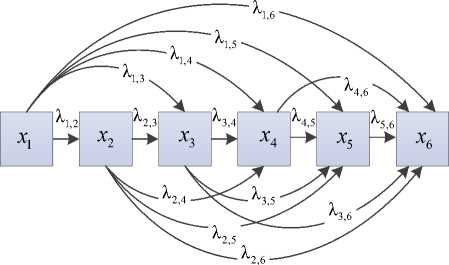
Рисунок 5. Граф, моделирующий процесс деструкции полимера с ММР из шести фракций

Figure 5.Graph modeling the process of destruction of polymer with MWD with six frасtiоns

Структурная схема математической модели процесса деструкции полимера в виде в формате MathWorks Simulink™, реализующая математическую модель (6) на основе методик [5, 6], представлена на рисунке 6.

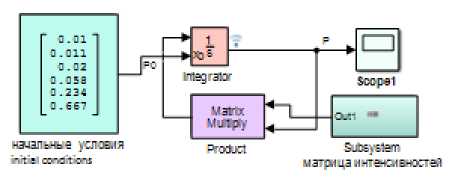
Рисунок 6. Структурная схема математической модели в среде Simulink

Figure 6. Structural diagram of the mathematical model in the Simulink environment

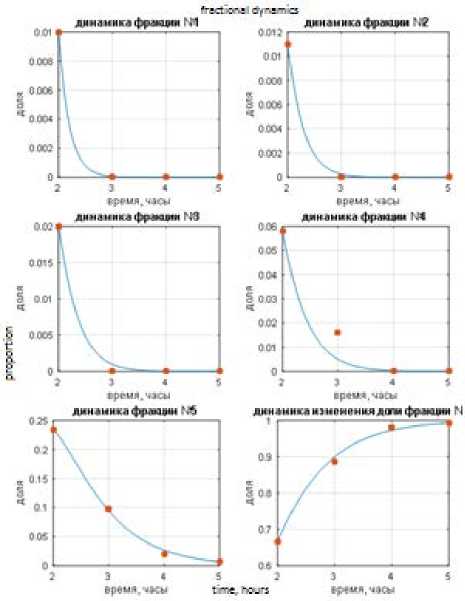
Рисунок 7. Динамика изменения фракционного состава какого-то полимерав ходе процесса деструкции (расчетные (-) и экспериментальные ( • ) данные)

Figure 7. Dynamics of changes in the fractional composition of a polymer during the destruction process (calculated (–) and experimental (•) data)

Для численного поиска значений параметров минимизировалось среднеквадратичное отклонение расчетных данных от экспериментальных по каждой фракции

MN ₂

• ⁵    = ZZ ( ^РДt ) exper — P j ( t - ) calc ) -T^ min , (7) j = 1 - = 1

где M, N – количество фракций и точек контроля при заданном времени деструкции соответственно.

Для минимизации критерия (7) использовался нелинейный метод наименьших квадратов на основе алгоритма Левенберга-Марквардта [7] из библиотеки Optimization Toolbox Math Works™ [8].

Полученные в результате параметрической идентификации на основе данных натурного эксперимента значения λi,j позволяют, задаваясь начальным фракционным составом, рассчитывать долю каждой фракции в ходе процесса деструкции (рисунок 7) .

Выводы

Рассмотренное матрично-графовое представление структуры математической модели процесса деструкции полимеров позволяет упростить составление модели и ее программную реализацию в случае большого количества вершин графа, описывающего процесс деструкции.

Кроме того, использование матрично-графовой модели делает возможным решать типовые оптимизационные задачи на графах для анализа интенсивности процессов деструкции в пределах заданных